基于遗传算法的AlSi10Mg合金本构方程参数反演

张旭升，伊兆锋，秦睿贤，，陈秉智 ，李世文

(1.大连交通大学 机车车辆工程学院，辽宁 大连 116028；2.中车唐山机车车辆有限公司 技术研究中心，河北 唐山 064000)①

仿真模拟是预测结构在动态冲击载荷下承载响应的主要技术手段.合理准确的本构参数是结果可信的关键之一，特别是本构模型能够准确地模拟材料进入塑性阶段之后的力学行为.以往的研究中学者们提出了较多的本构模型[1-2]，其中Johnson-Cook本构模型由于形式简单，物理意义明确，得到了广泛应用.

确定本构参数主要有两种方法，一是以正向拟合为代表的传统方法，即将本构方程中的硬化、应变率和温升效应进行解耦，逐一确定每种效应参数，最终确定所有参数值.部分材料的本构参数确定得到了较好的拟合效果[3-4]，但也存在拟合数据与试验数据偏差较大的情况[5-6].有研究表明,应变率在103～104s-1时，材料的流动应力会因塑性变形机制从位错滑移转变为位错拖拽而显著增加.传统的试验拟合本构参数不能准确预测变形机制转变引起的应力变化[7]，得到的本构参数往往需要进行修正才能应用于工程模拟, 参数修正一定程度上也降低了模型适用性[8-11].此外，传统的正向方法从拿到数据波形到最终得到本构参数，中间数据处理环节较多，容易引入人为处理误差积累.柳爱群等[12]指出该方法存在每条曲线之间缺乏有机联系等问题，并且提出采用最优化算法来识别材料参数，采用试验方法确定参数的值作为优化的初始值能够有效地提高优化效率.因此就需要对应变率系数进行修正.

另一种方法即反向逆求方法.该方法最初主要应用于混凝土[13]、复合材料[14]等非金属材料的参数获取中，后来也越来越多地用于金属材料的本构参数确定[15-17].Gelin等[18-19]探讨了铝合金材料黏塑性参数的反求计算方法,在优化过程中首先采用了改进的 Levenber-Marquardt(LM)算法，反求了不同应变、应变率和高温等复杂变形条件下的本构模型参数.吕思雨等[20]对7N01铝合金进行准静态拉伸试验，忽略应变率和温度的影响，采用曲线拟合和有限元仿真优化相结合的方法反求Johnson-Cook本构参数，发现遗传算法和自适应响应反求材料参数的方法优化收敛速度快，且精度满足要求.魏刚等[21]通过拟合试验数据，结合Taylor撞击试验反算得到调质处理45钢的本构参数.

关于铝合金的动态本构参数研究较多，但是采用优化方法确定AlSi10Mg参数的不多.因此本文开展AlSi10Mg的准静态拉伸和动态压缩试验，基于二波公式对试验数据处理，采用正向方法确定材料的Johnson-Cook本构参数.建立SHPB数值仿真模型，以试验波形为基准，采用NSGA-II算法反求本构参数，并对不同方法获得的本构参数进行对比，获取更为准确的材料本构方程，为相关结构的动态冲击分析提供参数.

1 AlSi10Mg静动态力学性能

1.1 准静态拉伸

按照标准GB/T 228.1—2010[22]的拉伸试验方法对AlSi10Mg试件进行准静态单向拉伸试验.试验采用标准P1试件，夹持端长宽均为20 mm，标距为25 mm，拉伸区域宽度为10 mm，过渡圆角半径为20 mm.采用Epslion接触式引伸计(标距25mm)夹持,拉伸速度为0.15 mm·min-1,名义应变率为1×10-4s-1.准静态单向拉伸试验在岛津AGS-X试验机上进行,试验环境温度为室温.AlSi10Mg材料真试工程应力-应变曲线见图1.

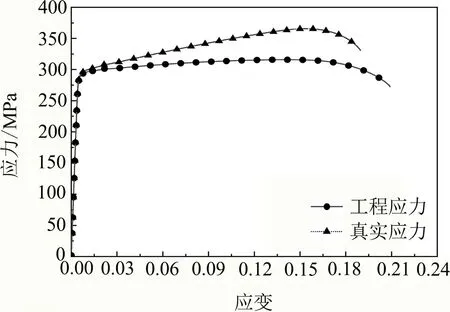
图1 AlSi10Mg材料真试工程应力-应变曲线

1.2 SHPB试验

分离式霍普金森压杆(Split Hopkinson Pressure Bar，SHPB) 试验系统可进行材料在中高应变率(102～104s)下动态力学性能试验,SHPB试验装置示意图见图 2，本次试验环境为室温，通过控制气室压强进而来实现不同应变率下的加载，压杆波速为5 090 m/s，采样频率为1 MHz.输入透射杆、子弹杆均使用铝杆.子弹杆、入射杆和投射杆杆径均为16 mm，长度依次为200 mm、1 000 mm、1 000 mm.试件直径为7 mm，厚度为3.5 mm，试件的加载表面平行度误差不超过0.01 mm.

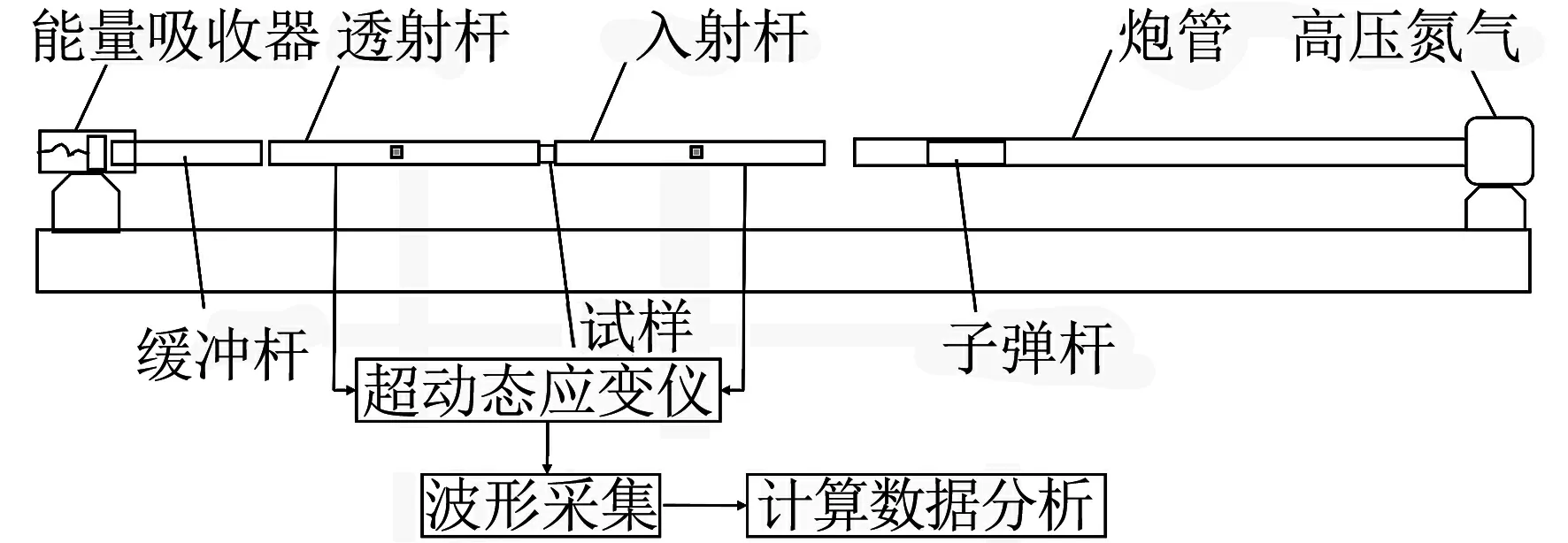
图2 SHPB试验装置示意图

试验应变片采集到的电压信号波形需要转化至应力波，供后续参数反演使用.

基于一维应力波传播理论与均匀性假设，试验数据处理采用经典二波公式[23]，各参量关系表达式见式(1)～式(3).

根据经典二波公式，试件的真实应力、应变和应变率主要取决于反射波和透射波的应变响应，然而处理数据的过程中需要选择入射波和透射波形的有限区段，在确定有效区间的过程中存在较大的主观性和随机性;同时,不同区间的选取也会直接造成本构参数的差异，进而带来本构参数误差积累.

不同应变率下AlSi10Mg的真实应力-应变曲线见图3.从图中可知，材料的流动应力会随应变率的增加显著提高，表明AlSi10Mg具有一定的率敏感性，但是随着应变率的增加，应力强化程度有所下降.

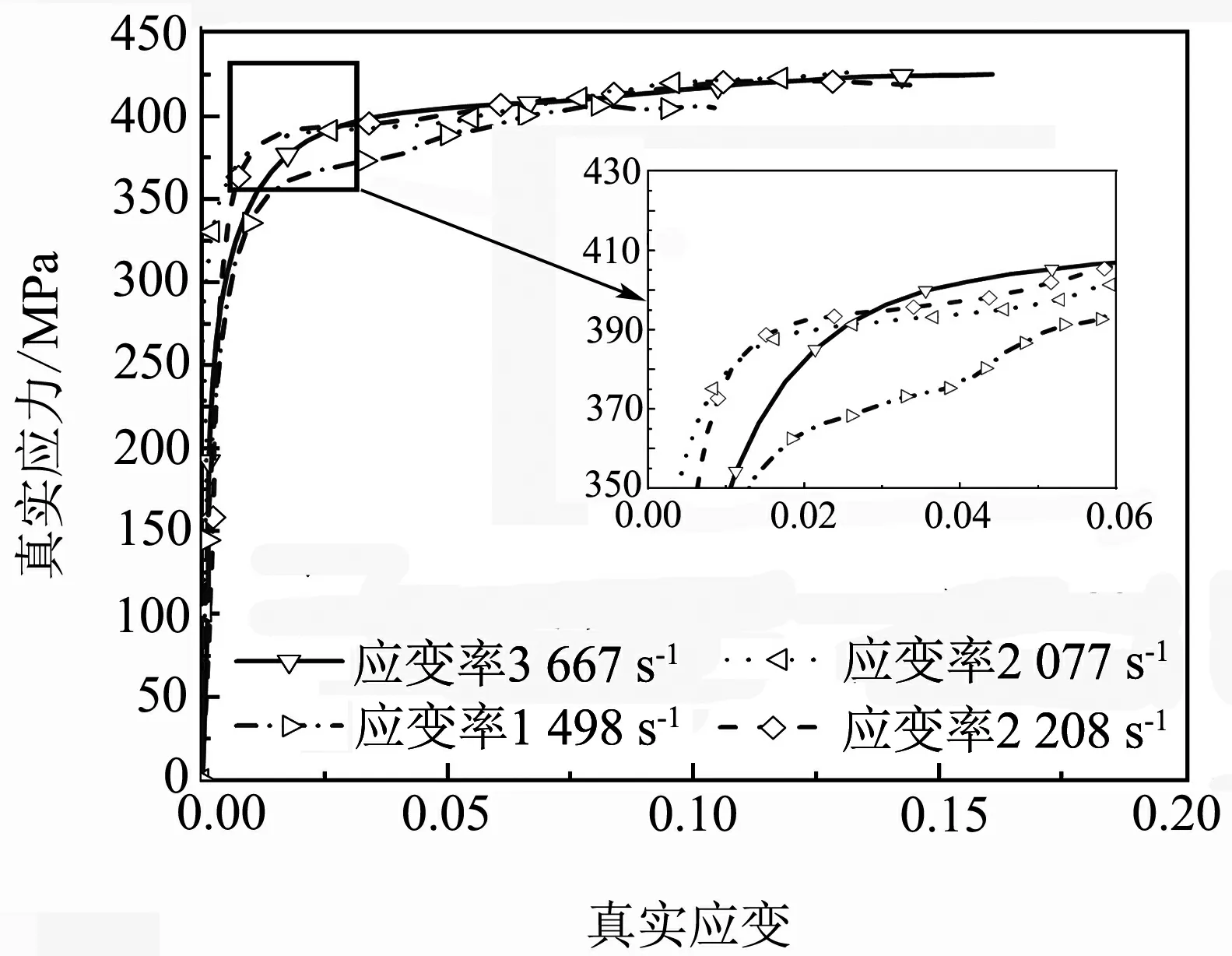
图3 不同应变率下AlSi10Mg的真实应力-应变曲线

2 Johnson-Cook本构参数标定

Johnson-Cook本构模型可表征大应变、高应变速度和高温变形下金属材料的准静态和高速变形.本次SHPB试验中不考虑材料的温度效应，Johnson-Cook模型可简化为：

(4)

(5)

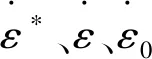
拉伸试验可以直接确定参数A为293.5 MPa.对式(6)两边同时对数处理即可得到线性关系式(7)，取不同有效应变下的应力做计算，进行拟合确定B=287.2MPa，n=0.717.

σ=A+Bεn

(6)

ln(σ-A)=nlnε+lnB

(7)

确定A、B、n三项参数之后,式(4)变换得到式(8),即可获得流动应力强化系数与无量纲应变率对数的线性表达式：

(8)

在不同应变率下分别提取多组有效应变下的流动应力并且对数据进行拟合，发现不同应变下的应变率效应参数是不一致的.通过计算得到不同应变下，应变率效应参数的平均值C=0.013 487.

3 仿真模拟

3.1 有限元模型

根据SHPB试验装置中子弹杆、入射杆、试件和透射杆的真实尺寸在HyperMesh中建立冲击试验对应的有限元模型(图 4)， 采用8节点六面体实体网格进行建模，SHPB压杆轴向单元尺寸为1 mm，径向网格尺寸为2 mm，试件的径向轴向网格尺寸为0.5 mm.

图4 有限元模型

入射杆、透射杆和子弹杆采用LS-DYNA软件材料库中线弹性模型(MAT1_ELASTIC)模拟，密度为2 700 kg·m-3，弹性模量为72 GPa，泊松比为0.3；试件采用98号材料本构(MAT_SIMPLIFIED_JOHONSON_COOK)，密度为2 700 kg·m-3，弹性模量为72 GPa，泊松比为0.3，A=293.5 MPa，B=287.2 MPa，C=0.013 487，n=0.717.

在子弹、入射杆、试件和透射杆之间的接触行为均采用面面接触(SURFACE-TO-SURFACE)模拟.在关键字INITIAL_VELOCITY_GENERATION中对子弹施加冲击初速度，应变率为2 208 s-1时动态冲击对应冲击杆的初速度为19.6 m/s.入射杆和透射杆应变片对应位置单元输出应力波形，用于采集数值模拟中的应力波信号响应.SHPB试验采样频率为1 MHz，数值仿真的应力输出间隔设为0.001 ms.

3.2 仿真结果

入射杆、透射杆对应输出点的应力波，见图5.从图中可知，在0.099 ms时，子弹压缩入射杆，产生压缩波沿入射杆向试件方向传播，尚未传达至试件；在0.25 ms时，应力波通过入射杆传递至试件与入射杆的交界面，试件产生塑性变形，应力波一部分在界面处反射，另一部分应力波透过试件传递至透射杆；在0.349 ms时，反射波和透射波依次沿入射杆和透射杆传播.试件加载过程不同时刻试件应力分布见图6.在0.25 ms时，试件由应力波传递到试件与入射杆的接触面，产生压缩应力；在0.25～0.32 ms时试件进入到均匀变形阶段；0.35 ms时刻后，试件逐渐进入应力卸载阶段.数值仿真结果符合试件加载物理过程，将作为后续本构方程参数反演的原始数据.

图5 入射杆、透射杆对应输出点的应力波

图6 试件加载过程不同时刻试件应力分布

4 本构参数反演

4.1 反演问题的描述

分别提取试验和仿真结果中入射波和透射波信号，计算两种信号的差方和(Sum of Squared Difference，SSD).本构参数反演流程见图 7.传统的正向确定本构参数的方法不仅需要复杂的数据处理流程，而且人为误差会随数据处理的过程不断累积.反演方法只需要将仿真和试验得到的应力波形进行波形统一后导入建立好的优化模型，以试验仿真的应力响应差方和作为优化目标，软件自动调用不同本构参数下的仿真模型，计算寻优后最终得到理想的本构模型参数，从而显著减少正演方法带来的人为误差累计.

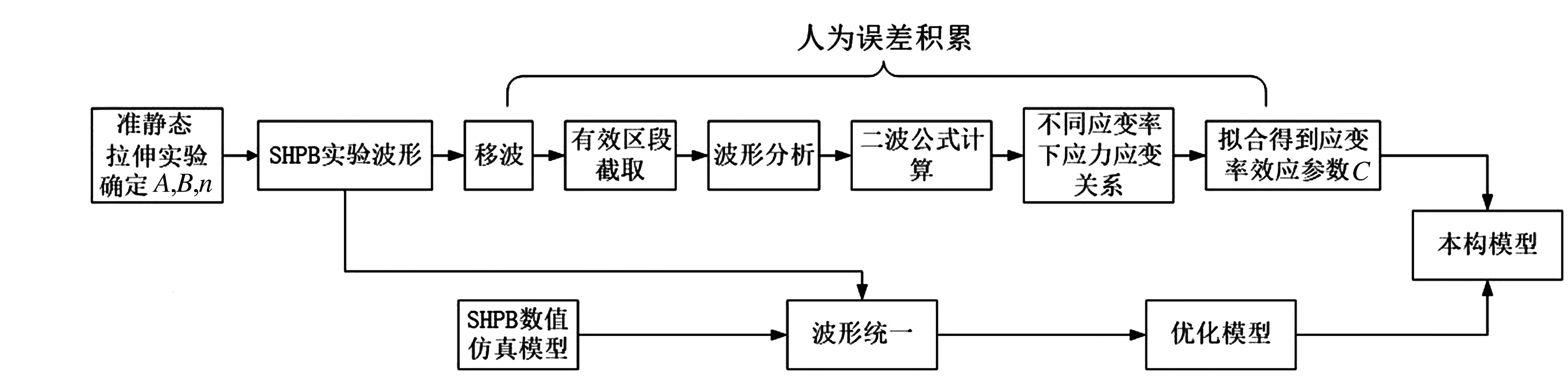
图7 本构参数反演流程

本构参数反演问题的数学模型见式(9)：

(9)

式中：i为应力响应数据点编号；ti为第i个应力单元输出时刻；A、B、n、C均为反演的本构参数，Yi为ti时刻试验的应力值.

NSGA-II的快速非支配排序算法保证种群多样性的同时确保了优良个体的保留率，从而提高优化结果的精度[24].种群规模为20，遗传代数为30，交叉率为0.9.设计变量A、B、n的设计域参考静态拉伸得到的试验数据来确定，应变率效应参数C的设计域根据铝合金的经验值确定.

4.2 反演结果

最优解的Pareto分布见图 8，可以发现入射杆应力波信号SSD降低的同时意味着透射杆应力波信号SSD的提高，由于比例因子不同，无法在双目标下均衡择优，将入射杆和透射杆上应力响应SSD按式(10)进行归一化处理，建立均衡评估函数来确定最优解，归一化处理结果见图 9.

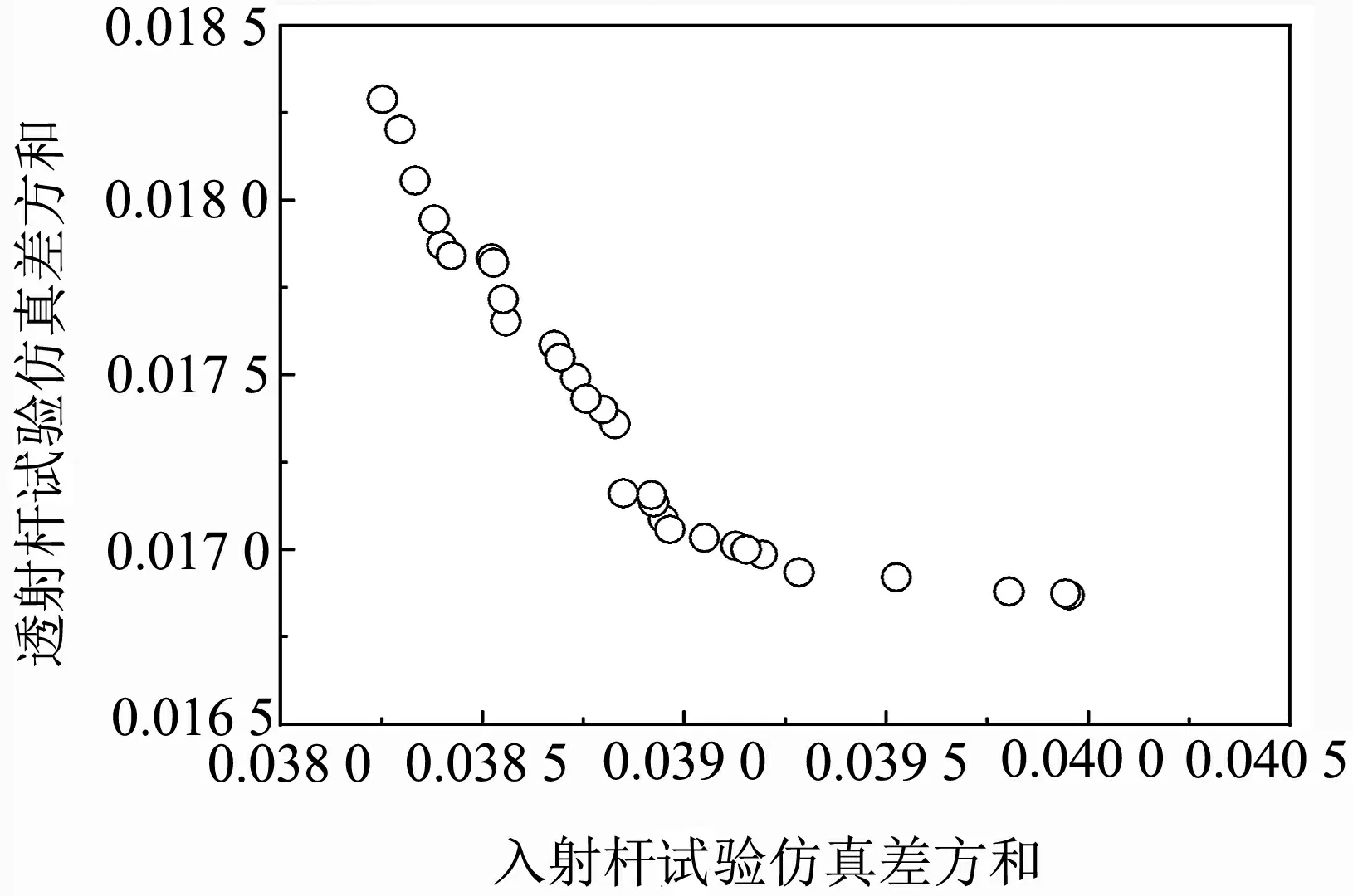
图8 应力波信号SSD的Pareto前沿

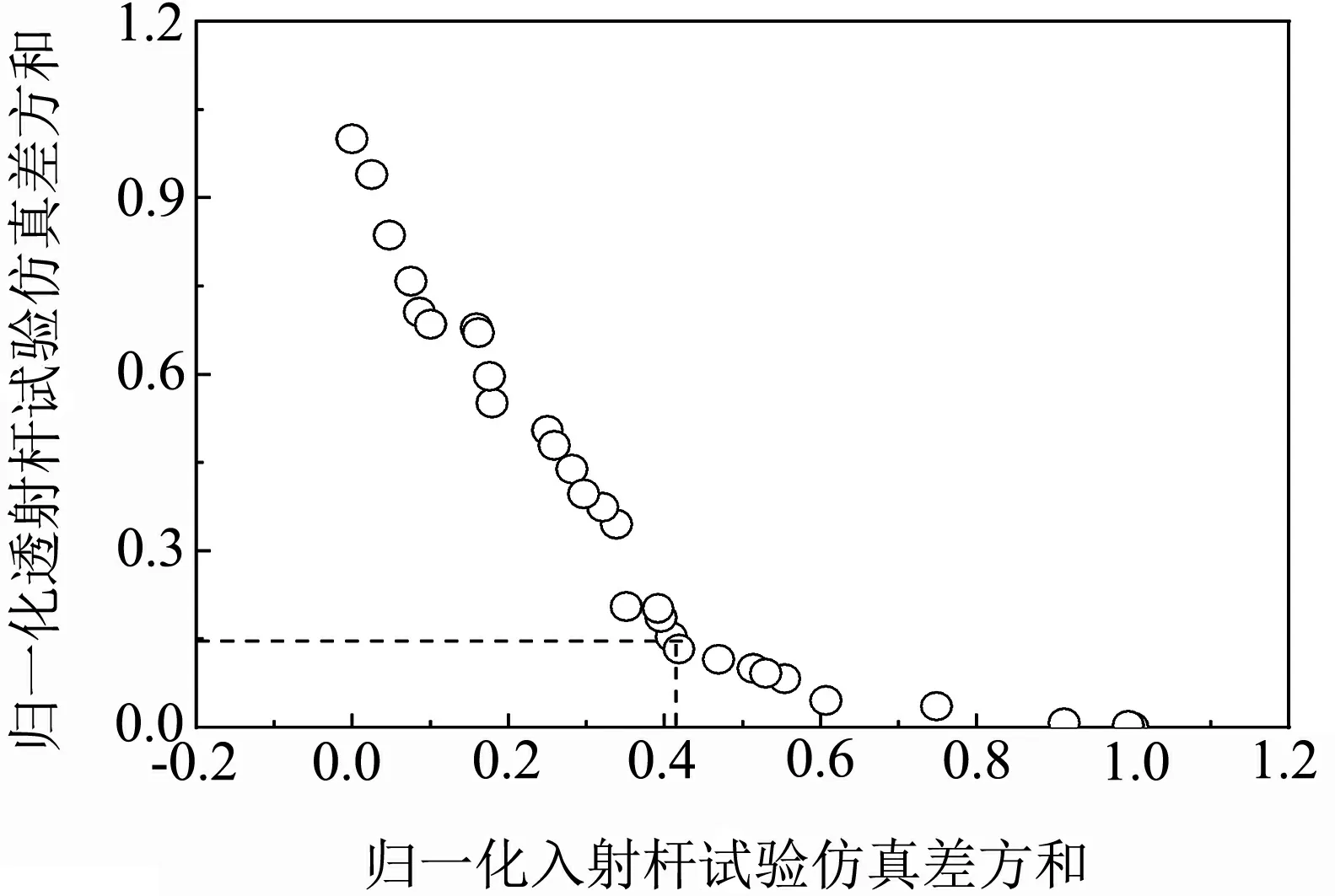
图9 归一化处理结果

(10)

二波公式与反演方法确定的应力响应和试验波形响应结果对比见表1，可知经过参数反演确定的SSD明显下降，入射杆和透射杆的SSD降幅分别为19.5%，15.2%，说明反演方法可在一定程度上降低传统方法的累计误差.

表1 不同算法下的响应结果对比

4.3 反演结果验证

分别对采用传统方法和优化方法确定的本构参数进行SHPB试验仿真，提取入射、透射信号，并与试验信号进行对比(图10)，可以发现，参数反演来确定本构的应力波信号更加接近试验信号，特别是透射信号其吻合度较高.由于反演是基于2 208 s-1应变率下得到的本构参数，为了验证该本构模型在其他应变率(1 493 s-1、2 077 s-1、3 667 s-1)与试验数据的一致性，分别进行了对应不同子弹杆冲击速度的SHPB压杆试验仿真，不同应变率下试验和优化后Johnson-Cook模型的应力响应对比，见图 11.

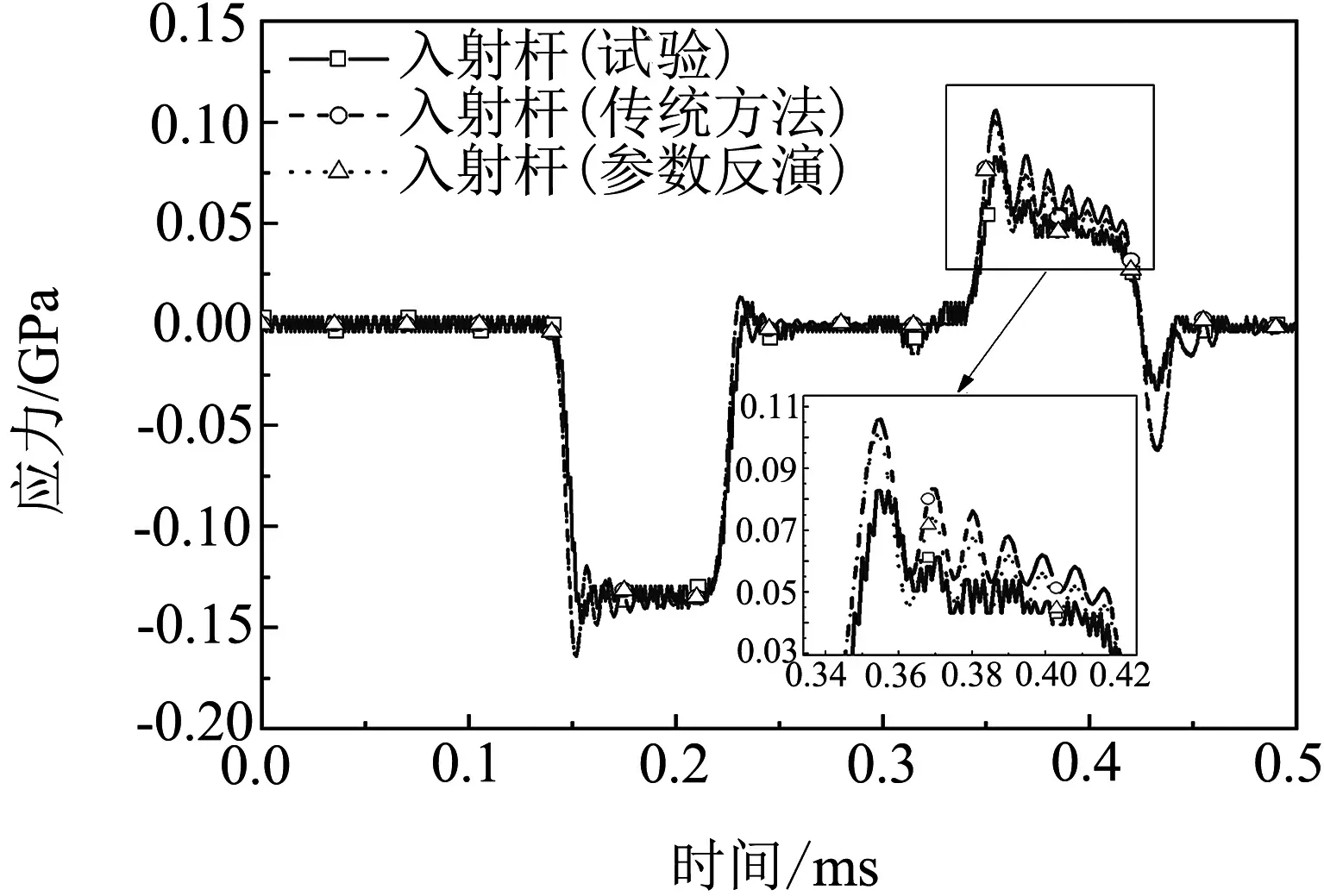
(a) 入射杆

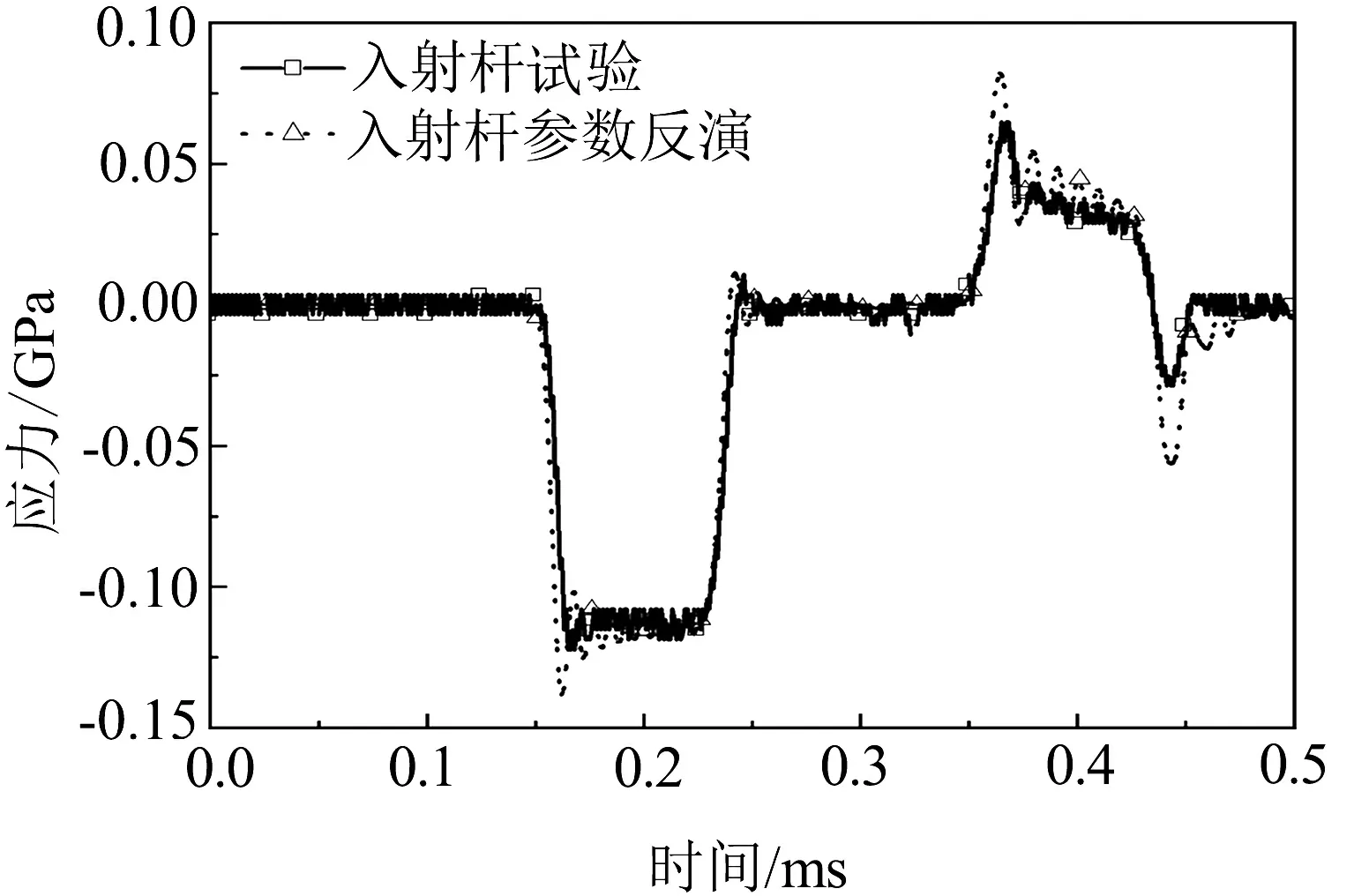
(a) 1 493 s-1

不同应变率下试验和正反演Johnson-Cook模型的应力-应变数据对比，见图12.传统方法得到的本构模型在3 667 s-1应变率下与试验结果相比偏小，而反演得到的本构模型在2 208 s-1和3 667 s-1应变率下基本与试验结果吻合，仅在2 077 s-1下流动应力略高于试验数据，表明反演后得到的本构模型更加适用于预测该材料中低应变率下的流动应力.鉴于此，本文虽然只探讨了用一种应变率下的应力响应信号做参数反演，但该方法于其他应变率应力信号响应和流动应力预测与试验数据的一致性均得到了验证，说明该方法具有一定的工程意义和适用.

图12 试验和正反演Johnson-Cook模型的应力-应变数据对比

5 结论

(1)采用反演方法确定的本构参数获得的应力波形更接近试验信号，适合应变率随着应变波动的情况中本构参数的确定，可以提高材料参数在工程分析中的适用性.结合有限元仿真模拟和优化算法对材料参数进行识别的方法有效地提高了参数确定的效率，降低了人为数据处理带来的累计误差.

(2)本文只探讨了用一种应变率下的信号做参数反演，未考虑多个应变率下的参数反演.但该方法用于其他应变率应力信号响应和流动应力预测与试验数据的一致性均得到了检验和验证.同时该反演流程不仅适用AlSi10Mg材料的本构参数识别，也为确定金属材料的动态本构参数提供了新的方案.