重载列车制动力判断标准及纵向冲动研究

2023-01-18刘博阳魏伟豆飞

大连交通大学学报 2022年6期

刘博阳，魏伟，豆飞

(1.大连交通大学机车车辆工程学院，辽宁大连 116028；2.国家能源集团朔黄铁路机辆分公司，河北肃宁 062350)①

重载铁路以运输效率高、成本低、低碳环保等优势，迅速成为国家战略性、先导性、关键性重大基础设施，在经济社会发展中的地位不言而喻.2万t列车作为当前重载列车的代表，面临编组长、开行密度大、线路情况复杂等问题，这些问题使得列车通过长大坡道、小半径曲线时的操纵十分困难.并且2万t列车操纵指导书均是参考部分试验结果，根据有经验司机的直观感觉制订而成，纵向动力学领域的研究尚有空间应用到重载列车开行中.

为确保重载列车的运行安全、探究其合理操纵方式，国内外众多学者开展了大量研究.Bentley等[1-2]针对列车空气制动系统的制动性能进行了分析预测；Wu等[3-4]分别介绍了其开发的列车制动仿真系统和列车运行模拟系统；孙翔等[5-6]分别用重载列车制动操纵技术和空气制动系统相关参数对列车制动的影响进行分析；邵军等[7-8]分别搭建了重载列车制动系统综合试验平台和基于Newmark-β算法的纵向动力学模型；曹记胜等[9-10]分别对重载列车采取缓解操纵、制动不同步性和坡道坡度对列车纵向冲动的影响进行分析；魏伟等[11]开发了列车空气制动与纵向动力学联合仿真系统，为制动系统和列车纵向冲动等研究提供有力帮助.上述研究均对重载技术的发展起到了极大的推动作用，仿真研究更是具有经济、安全、快捷的特点，尽可能减小研究的费用与周期，并实现了危险工况的安全模拟.虽然操纵方法的探究对仿真系统的精度提出了更高要求，但列车空气制动与纵向动力学联合仿真系统因其精度高、速度快的优势，已经成为大秦、朔黄铁路操纵优化、事故分析的重要工具，且该系统曾于2017年在国际纵向动力学评测中获得优异成绩[12].

朔黄铁路运营里程594 km，全线海拔高度差1 527 m.列车始发时及进入长大下坡道前要进行列车空气制动系统性能试验，检验列车管是否处于贯通状态以及判断制动力强弱[13]，为后续的操纵方式提供参考.制动能力强弱的判断极为重要，判断失误会造成列车被迫停车，严重影响运输效率和运行秩序.朔黄铁路2万t重载列车开行五年来，发生区间停车缓风的列车占比达34.3%.列车空气制动力判断失误导致列车未能在指定地点缓解是列车停车缓风的主要原因.因此，本文从纵向动力学角度对2万t重载列车制动力判断标准进行探究，并分析了列车在长大下坡道循环制动时产生较大车钩力的原因，对司机的操纵技能提升、保障运输效率和运行安全以及列车自动驾驶技术的研发具有重要的现实意义.

1 列车纵向动力学及空气制动系统

1.1 列车纵向动力学模型

在研究列车纵向动力学时，将列车模型化为多质点的质量弹簧阻尼系统，只考虑列车的纵向自由度.取某单一机车车辆为研究对象分析其受力情况，其受力图见图1.

图1 单一机车车辆受力图

考虑到列车空气制动力、运行阻力等是被动受力，仅在列车有速度或者有运动趋势时才起作用，这些力不会使机车车辆发生运动，仅是阻碍车辆运动，机车车辆运动方程如式(1)～式(3)：

F1i=FGi-FGi+1+FLi-FWi

(1)

(2)

(3)

1.2 列车空气制动系统模型

列车的空气制动系统中，气体在各管路、缸室内流动，将其离散为一系列管路、容器，将分配阀模型化为各管路与容器间连接通路的控制装置.假设管路内壁是刚性的，管路内为一维、非等熵不定常的气体流动，在不计空气重力的情况下，根据气体流动的连续性、质量守恒、动量守恒定律和能量守恒定律建立描述气体状态的方程组，如式(4)：

(4)

式中：ρ、u、p、a、k、D、F、f、q、x、t分别为气体密度、流速、压强、声速、比热比、管路直径、管截面积、管内壁摩擦系数、传热率、距离和时间.将上述偏微分方程组使用特征线法转化为常微分方程组后求解.引入的特征线方向、边界条件以及分配阀具体模型请参见文献[15-16].

2 朔黄铁路2万t重载列车制动力判断与调整

宁武西—龙宫区段为连续的长大下坡道，坡度大于-9‰的下坡道占该路段的90.1%，长梁山隧道的长度更是达到12 km，且为坡度10.2‰的长大下坡道，是整个朔黄铁路的操纵困难区间之一，也是制动力判断失误停车发生最多的区段.列车在该区段时的制动力判断是否准确直接影响列车后续操纵方式，对列车的安全运行起着关键性的作用.本文以朔黄铁路日常开行的2万t重载列车为对象，分析制动力判断方法.列车编组为1HXD1+108辆C80+1HXD1+108辆C80+可控列尾，牵引总重为21 600 t.

2.1 现行制动力判断方式及标准

朔黄铁路2万t重载列车精细化操纵指导书中提出，宁武西—龙宫区段列车初制动地点在k20+000～k20+500处，制动初速为65 km/h，空气制动减压量为50 kPa.长梁山隧道内和龙宫站内缓解地点分别位于k22+500～k32+500和k42+300～k43+200处.在正常情况下，宁武西—龙宫区段采用三把闸操纵方式；若列车制动力较弱，则采用两把闸操纵方式.

列车在神池南出站后运行至k9+800～k10+000处，速度达到70 km/h，空气制动减压为50 kPa，以空气制动指令发出后50 s时的速度初步判断列车制动力强弱，此时列车速度在64 km/h以上、63～64 km/h之间、63 km/h以下时，判断列车制动力分别为偏弱、适中偏弱、偏强[17].但该处试闸结果只作为初步判断制动力的依据，需以列车在k20+500处的试闸结果作为主要判断依据.

k20+500处的试闸过程为：待列车运行至k20+500处，速度达到65 km/h时，空气制动减压为50 kPa，再生制动力为400 kN.根据列车制动后的走行距离和降速情况判断制动力强弱，判断标准参照文献[17]：空气制动后运行至k23+300、k23+300～k23+800、k23+800～k24+300、k24+300处，速度能够降至40km/h的列车，分别判断为制动力较强、适中、偏弱及较弱.

2.2 制动力判断方式优化思路

在实际开行中2万t重载列车制动系统特性千差万别，特别是缓解和制动前制动系统的压强分布，直接影响后续缓解动作的传递过程和非首次制动的制动能力.为了获取这种受再充风能力和漏泄等多因素影响的制动系统特性，本研究在制动系统特性上采用列车空气制动与纵向动力学联合仿真系统实现.该系统可动态计算制动系统管路中的压强，保证仿真系统中列车制动缓解时压强变化与真实列车制动系统压强变化一致，能够真实反映制动缓解时制动系统的压强分布规律，以及这种压强分布对制动和缓解的影响.

现行制动力判断方式不足主要表现在：①列车运行至k20+500时，在前序操纵中已经施加两次空气制动，由于缓解过程中再充风时间不同造成列车管压强分布在列车运行至k20+500处时存在较大差异，进而导致列车在k20+500处试闸判断不准确.②实际运行中可能存在漏泄等情况，导致列车在循环制动前列车管压强分布不同.③在k20+500处试闸需要在短时间内及时判断制动力强弱，选择该区间接续的操纵采用何种方式，司机反应时间较短.

试闸时应固定试闸速度、地点、空气制动减压量、再生制动力值等.由于列车在神池南出站后首次试闸(k9+800～k10+000处制动)前列车管为充满状态，此次试闸对列车制动力的判断较为准确.其次，列车进入长梁山隧道前的列车管压强将大幅影响循环制动中制动力的强弱.由于朔黄铁路2万t重载列车装有可控列尾装置，司机可实时监控列尾压强，因此可将列车在进入长梁山隧道前的k20+000处的列尾压强作为判断依据之一，结合神池南出站后首次试闸结果综合判断列车制动力强弱.

2.3 制动力判断方式仿真及优化结果

参照朔黄铁路2万t重载列车精细化操纵指导书，首先对2万t重载列车神池南出站后k9+800～k10+000处的试闸进行仿真.在仿真过程中通过设置不同参数来模拟不同制动能力的列车，固定试闸地点在k9+800处，制动初速为70 km/h，空气制动减压为50 kPa，记录列车施加空气制动后行驶至k10+800处的速度，列车在该处速度的差异代表列车制动力强弱不同.k9+800处试闸仿真结果见表1，根据列车制动后到达k10+800处的降速情况可以初步判断制动力强弱，若列车降速较快则制动力较强，表中从左至右的列车制动力逐渐减弱.

表1 k9+800处试闸仿真结果

现行制动力判断方式中未考虑列车管压强分布对列车制动性能的影响，仅依靠试闸时列车的走行距离和降速情况判断列车制动力强弱，所以在仿真系统中对上述试闸列车在宁武西—龙宫区段k20+000处分别设置不同列尾压强进行仿真，模拟列车在实际运行中的真实情况，通过分析总结该仿真工作并结合仿真中宁武西—龙宫区段的操纵方式得出制动力判断方式.

在仿真过程中固定宁武西—龙宫区段第一把闸制动地点为k20+500处、制动初速为65 km/h、制动时再生制动力为400 kN及缓解时再生制动力为300 kN，并在循环制动时保证足够的再充风时间，以保证列尾压强不低于580 kPa，合理调整列车后续操纵方式.

在仿真中若列车在宁武西—龙宫区段可采用三把闸操纵安全通过，则该方案中列车制动力判断为较强.若列车在宁武西—龙宫区段采用两把闸、三把闸操纵均可安全通过，则该方案中列车制动力判断为适中.若列车存在无法在长梁山隧道出口(k32+500)前进行第二把闸缓解、列车在第三把闸制动时降速过慢导致控速困难等情况时，该仿真方案中的列车采取两把闸操纵且列车制动力判断为较弱.

对神池南出站后首次试闸(k9+800处制动)仿真中不同降速情况、k20+000处不同列尾压强的列车运行至宁武西—龙宫区段的操纵方式加以总结，得出更为准确的制动力判断方式.各工况的列车在宁武西—龙宫区段的操纵方式仿真结果见图2.

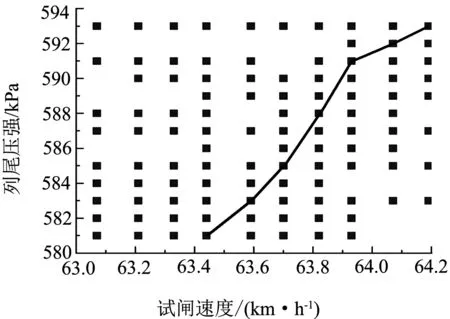
图2 宁武西—龙宫区段操纵方式仿真结果

图2中横轴为不同制动力列车在k9+800处试闸，列车行驶至k10+800处的速度，纵轴为列车运行至k20+000处的列尾压强.优化后的制动力判断标准为：综合试闸速度和固定位置的列尾压强两个因素判断列车制动力强弱，图中实线为列车制动力强弱的分界线；位于分界线上的方案，列车制动力判断为适中，可采用三把闸或两把闸操纵方式；位于分界线左侧的方案，列车制动力判断为较强，宁武西—龙宫区段采用三把闸操纵方式；位于分界线右侧的方案，列车制动力判断为较弱，宁武西—龙宫区段采用两把闸操纵方式.

该列车制动力强弱的判断方式相较现有方式的优势在于将列尾压强变量作为判断依据之一.依据出站试闸时施加空气制动后列车运行至固定位置的速度和循环制动前的列尾压强综合判断列车制动力强弱.相较于现阶段依靠司机经验判断列车制动力的方式，该制动力判断方式具有数据支撑，对制动力判断较为准确，可有效避免因制动力判断失误造成停车缓风.

3 列尾压强对2万t重载列车纵向冲动的影响

在上述仿真中发现，不同列尾压强的列车缓解时纵向冲动水平存在差异.由于实际开行中列车运行至宁武西—龙宫区段k20+000处时，多数列车的列尾压强均低于593 kPa，故选取在k9+800处试闸时试闸结果相同，而在k20+000处列尾压强分别为585 kPa、589 kPa、593 kPa的列车进行分析.仿真计算中待这三种工况下列车运行至k20+500处，施加50 kPa减压量的空气制动，制动初速为65 km/h，待速度降至35 km/h时缓解，各工况再生制动力施加方式一致，并完成后续循环制动，比较各工况制动缓解过程中列车最大车钩力.三种工况下的列车中每辆车的最大车钩力沿车长分布曲线见图3.

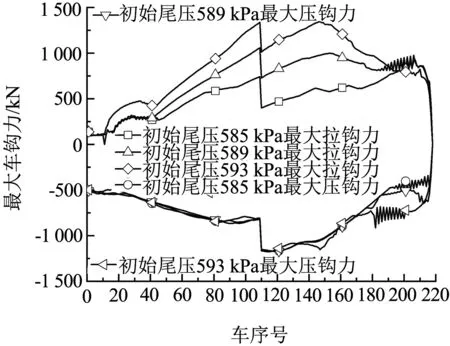
图3 三种工况下最大车钩力沿车长分布曲线

图3中的纵轴负值为压钩力，正值为拉钩力，三种工况下列车最大拉钩力均发生于109车 (从控机车前钩)，最大压钩力均发生于110车(从控机车后钩).初始列尾压强分别为585 kPa、589 kPa、593 kPa三种工况时，列车最大拉钩力分别为742 kN、1 058 kN、1 337 kN，最大压钩力分别为1 161 kN、1 150 kN、1 166 kN.初始列尾压强为585 kPa、589 kPa时的工况与593 kPa工况相比，最大拉钩力分别减小44.5%与20.9%，而最大压钩力在三种工况下区别并不明显.

图4为三种工况下列车109车、110车车钩力随位置变化曲线图.由图可知，三种工况下列车最大拉钩力均发生于第一把闸缓解时，且最大拉钩力随着初始列尾压强的升高而增大；最大压钩力分别发生于主控机车位于k42+497、k42+498、k42+534处，此时从控机车位于k41+167、k41+168、k41+204处.在该区段坡道千分数由-11.2‰、-9.3‰变为-2.0‰再到-1.5‰，坡道千分数变化最大位置为k41+136处，而110车最大压钩力发生位置同样位于该位置前后.此时列车前部车辆所处坡道较缓，而后部车辆处于坡道为-9.3‰的下坡道，整列车位于凹形坡上，列车后部车辆所受势能远大于前部车辆，后部车辆相对前部车辆向前涌动，加之此时列车为空气制动配合电制动的状态，导致列车在该位置产生大的压钩力.

(a) 109车

对该区段循环制动中产生的最大拉钩力进行分析，三种工况下列车第一把闸制动缓解过程均位于坡道-10.2‰的长大坡道，且制动位置、制动初速、缓解速度、再生制动力施加方式及列车管减压量均相同，因此考虑影响最大拉钩力的因素是初始时刻列尾压强的差异.缓解特性中的缓解波速影响整列车的缓解能力，也是影响列车缓解时拉钩力的主要因素，为探究这种特性每隔十车输出一个车辆的制动缸压强，并根据开始排气时间绘出缓解传播特性.

图5为三种工况下列车在第一把闸缓解时的缓解传播特性曲线，图中时间是所取车辆制动缸开始降压时间相对缓解指令发出时间的滞后值.列车缓解时主控机车向后充风，从控机车同时向前、后两个方向充风，致使前、中部车辆缓解较快，而后部车辆缓解存在滞后.当前部车辆缓解而后部车辆未及时缓解时，会导致列车产生较大的拉钩力，这也是缓解时列车产生拉钩力的主要原因，缓解波速的加快有利于提高列车缓解的同步性，减小缓解时的拉钩力.由图5可知，初始列尾压强为585 kPa、589 kPa、593 kPa三种工况的列车分别在22.3 s、24.4s 、27.4 s内开始缓解，各工况后80辆车开始缓解时间均明显晚于前、中部车辆，其中从控机车前部车辆均在10 s内开始缓解，而从控机车后部车辆平均开始缓解时间分别为17.8 s、19.2 s、20.9 s，初始列尾压强为585 kPa工况的列车相较于初始列尾压强为589 kPa、593 kPa工况的列车缓解波速有所提高，缓解同步性较好.

图5 三种工况下第一把闸车辆缓解传播特性曲线

三种工况下的列车管压强分布曲线见图6.不同初始列尾压强的列车，列车管的压强分布也存在差异.由于列车前部108辆车由主控机车和从控机车同时供风，而后部108辆车只有从控机车供风.由图6可知，从控机车前部车辆列车管压强分布差异较小，而从控机车后部车辆列车管压强分布明显存在差异.其中初始列尾压强为585 kPa工况的列车后部车辆列车管压强分布曲线斜率最大，且列车后部车辆列车管压强均值最低；初始列尾压强为593 kPa工况的列车后部车辆列车管压强分布曲线的斜率最小，列车后部车辆列车管压强均值最高.

图6 三种工况下列车管压强分布曲线

在制动时列车管压强的分布不同会导致列车制动力的不同，表现为制动时制动缸压强存在差异.表2为第一把闸时三种工况下的列车以从控机车为界，前、后部车辆制动缸平衡时压强均值.由表2可知，各工况下的列车从控机车前部车辆制动缸平衡缸压均值差异较小，制动力基本一致；而初始列尾压强为593 kPa工况的列车相较初始列尾压强为589 kPa、585 kPa工况的列车，从控机车后部车辆制动缸平衡缸压均值的差值分别达到了7.4 kPa和16.2 kPa，从控机车后部车辆制动力明显存在差异.结合前文探究可知，三种工况下的列车，从控机车前部车辆缓解波速基本一致，且制动缸平衡压强差异较小；而从控机车后部车辆缓解波速和制动力均存在明显差异.当前部车辆缓解而后部车辆未及时缓解时，后部车辆的制动力较强会加剧缓解过程中的拉伸作用.初始列尾压强较高的列车，从控机车后部车辆相对前部车辆缓解滞后程度较大，且从控机车后部车辆制动力较强，二者因素的叠加导致较高初始列尾压强的列车缓解时拉钩力增大.