多风向角侧风下动车组明线运行的气动特性

王东屏, 赵洁,罗焕,刘超

(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.大连交通大学 机车车辆工程学院,辽宁 大连 116028)①

列车速度的提高使得列车与空气的相互作用变得更加强烈[1].在实际的车辆运行过程中，随着侧风风向角的增大，列车空气动力性能逐渐恶化，列车各项气动力迅速增大，影响了列车的横向稳定性[2].倾覆力矩的增大导致列车失稳而脱轨和倾覆[3]，行车的阻力增大，使得运营能耗增大，同时对列车高速运行的安全性、稳定性也带来重大影响[4].因此，为了使列车安全通过风区，必须开展侧风环境下的列车空气动力特性研究.

目前，许多学者都对高速列车侧风下运行进行了大量研究，李西安等[5]研究了在列车明线运行时，不同网格划分对计算结果的影响，并与风洞试验数据进行比较.同时研究了横风作用下、不同车速和风速下列车的气动性能变化规律.郗艳红等[6]研究了单列高速列车在明线横风环境中运行时的气动特性，将来流速度为60 m/s，风向角为3°和6°时列车模型气动力系数与风洞试验的数据进行对比，得出了横风风速和风向角及车速对列车气动特性的影响规律.高广军[7]研究了在强侧风作用时，车—路耦合条件下车辆的气动性能，在风向角为90°时，车辆受到的气动力最大，并且气动力随着车速和风速的增大而增大.

虽然上述文章对高速列车侧风明线运行的气动特性进行了大量的计算分析，但多为改变车速和风速来对列车气动特性进行分析，对于变角度的研究较少，且与试验数据的对比验证较少，所以仍然需要对多个风向角下列车的空气流场进行数值分析.

本文应用Fluent流体分析软件，在多风向角侧风环境下，对动车组三车编组的空气动力流场进行数值仿真，将表面测点的压力系数结果与风洞试验结果进行对比，研究不同风向角下列车的表面压力系数规律、流场速度及各项气动参数，为动车组侧风环境下安全运行指标的确定提供技术支持.

1 计算模型

1.1 几何模型

列车计算模型取三车编组，即：动力车+拖车+动力车，车辆之间以风挡连接.对列车某些局部结构进行简化处理，最大限度地呈现列车外形原貌.动车组整车计算模型见图1.

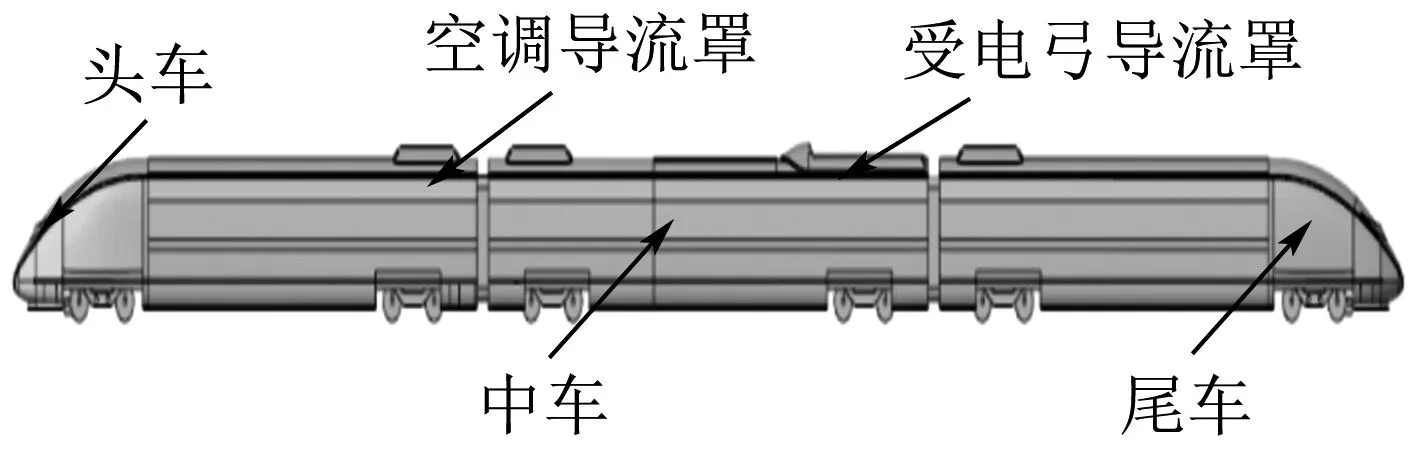
图1 动车组整车计算模型

为避免列车在尾部产生绕流，从而影响计算精度，设列车前端流场区域的纵向长度为25倍的列车高度，列车尾流区域的纵向长度至少大于2倍的列车总长度，计算域高度约为20倍的列车高度[8].考虑到侧风问题，扩大流域两侧面的区域，设侧方流场区域为2倍的列车总长度，最终确定整个计算区域为368 m×280 m×90 m.

1.2 网格划分

列车表面采用三角形网格划分，四周的矩形区域内部均采用几何适应性强的四面体非结构化网格，按照距离壁面的远近在车体周围划分三层区域：流域一、流域二和流域三，且网格大小依次减小.网格总数约为1 400万，整体流域的网格划分见图2.

图2 整体流域的网格划分

根据列车结构的不同，对其进行不同程度的网格划分， 研究车身特殊部位时需要对网格进一步加密，如列车头部、 空调导流罩、 受电弓导流罩及与车身连接处的细小结构，车头剖面网格划分见图3.

图3 车头剖面网格划分

1.3 计算方法

运用有限体积法对高速列车三维外流场进行数值模拟.列车周围流场为不可压缩、定常、黏性流体流动，故采用RANS方法[9]和RNGκ-ε双方程湍流模型对其空气流场进行仿真计算.计算方法使用SIMPLE来耦合压力—速度流场，对流项使用二阶迎风格式进行离散，黏性项为中心差分格式.

2 计算条件

2.1 边界条件

本文模拟列车在风洞中吹风试验的方式，给定边界条件，风速采用合成风[10].入口和迎风面设定为速度入口，风速为60 m/s；出口和背风面设定为压力出口，静压为0.根据列车与周围空气的相对运动，列车整体设置为无滑移壁面，地面设置为滑移壁面，滑移壁面的速度与车速大小相等、方向相反，以体现其与列车之间的相对运动.

侧风是风向与列车运行方向呈一定角度的环境风[10].列车侧风风向角示意图见图4，假定风向角为0°时以速度v吹向列车，设定方向为西北角度的侧风角度为负，西南方向的侧风角度为正.对风速为60 m/s、侧风风向角为-24°～+24°(间隔为3°)的17个计算工况进行了数值模拟.边界条件定义见表1.

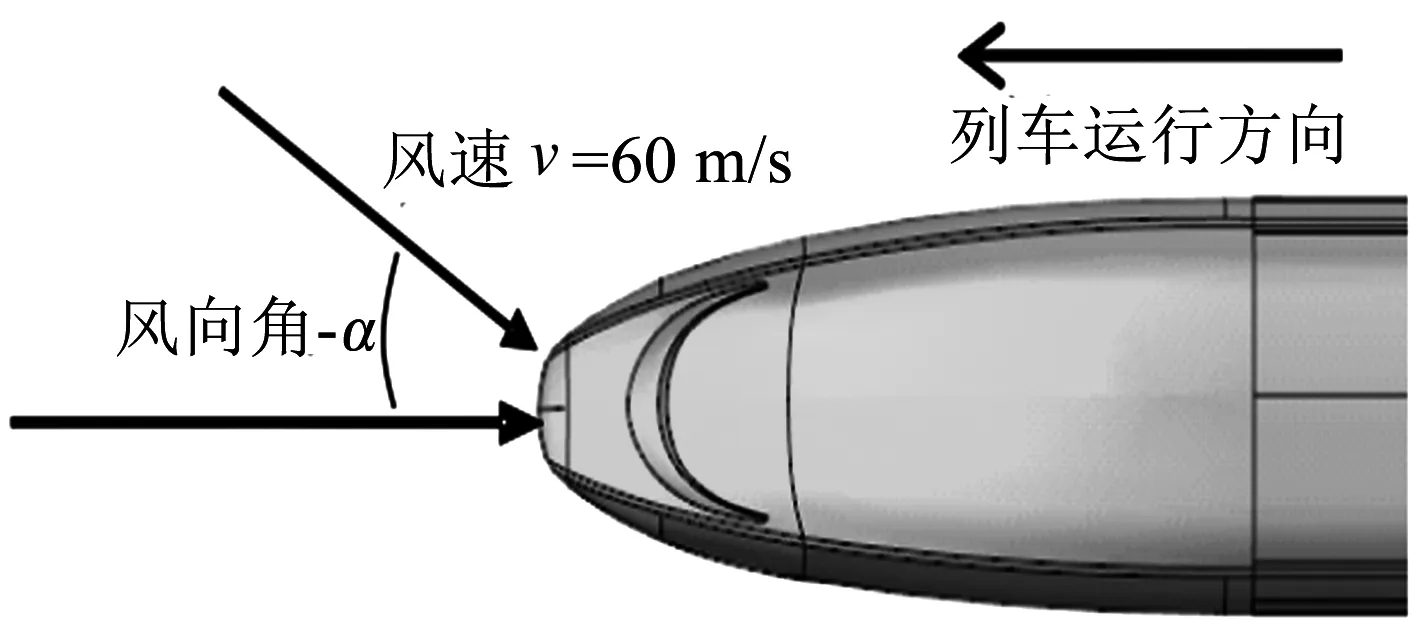
图4 列车侧风风向角示意图

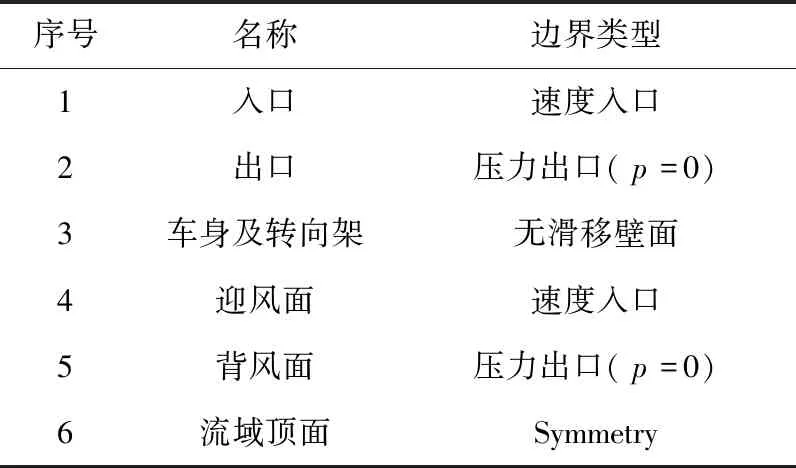
表1 边界条件定义

2.2 车身表面测点的建立

在风洞实验室中对动车组1/8 原型车进行了吹风试验[11].为了获得列车的表面压力系数，风洞试验中在列车车头和空调导流罩表面共计布置了若干个测压点，数值模拟中为保证建立模型测点的准确性和方便性，降低与风洞试验中列车车身测点表面压力系数对比的误差，因此在建立模型时设置与风洞试验相同位置的测点，测点通过在车身表面选取面单元方式创建.

3 结果分析

3.1 测点压力曲线结果对比

按照风洞试验报告内容选取的测点位置分别为头车鼻端前缘处和空调导流罩上表面中点处，将数值模拟得到相应的表面压力系数与风洞试验数据进行对比，图5为两个测点压力系数随风向角变化的曲线对比，风洞试验数据来源于参考文献[11].

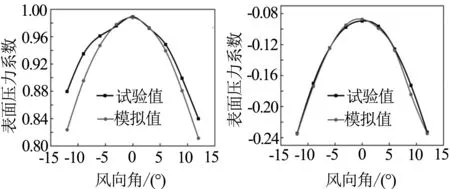
(a) 鼻端前缘处 (b) 空调导流罩上表面中点处

图5表明车身测点表面压力系数的数值计算结果与风洞试验的压力系数曲线变化趋势一致，但数值计算略小于风洞试验值.其表面压力对比的具体误差见表2.

表2 风洞试验与数值计算表面压力系数的比较

由表2可知，数值模拟与风洞试验的测点表面压力系数误差为10%左右，存在误差的原因主要有:数值模拟的几何模型与列车模型之间存在几何误差；数值模拟的送风方式为均匀风，而风洞试验的风场设定未完全按照均匀风送风；数值模拟的计算环境与风洞试验的试验环境无法保持完全一致.

可见，风洞试验与数值模拟结果之间存在合理误差，这验证了测点建立的准确性及模型计算方法的可行性，说明数值计算结果具有一定的参考价值.

3.2 侧风工况计算结果分析

3.2.1 车体表面压力分布

当列车在侧风环境中运行时，列车空气动力性能进一步恶化.表面压力分布规律不同于明线运行时的压力分布规律，不同风向角下车体表面压力云图见图6.

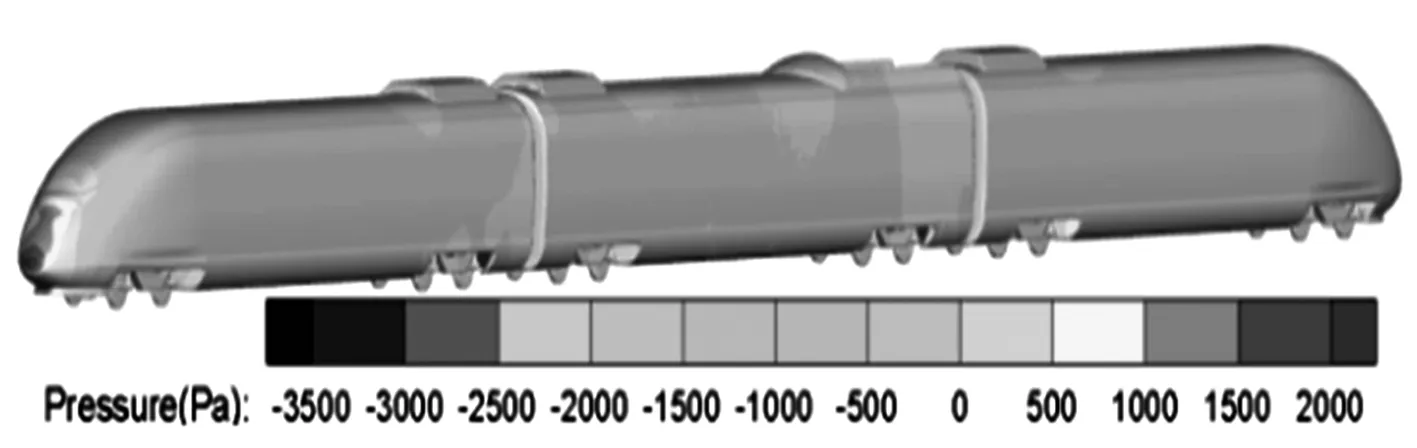
(a) 0°迎风侧列车表面压力云图

(c) -9°迎风侧列车表面压力云图

从图中可知，无侧风时列车车体表面压力分布的变化范围较小，迎风侧和背风侧负压范围较多，表面压力最大值位于头车鼻尖前缘点，此时车身表面最大压力为2 199 Pa，最小压力为-3 813 Pa.当风向角增大到-9°时，列车迎风侧大部分为正压区，背风侧均为负压区，头部的压力滞止点偏离列车前缘鼻端处，出现在车头鼻尖迎风侧处,此时最大压力为2 300 Pa，最小压力为-5 169 Pa，较无风时最小压力减小了36%.风向角进一步增大到-24°时，列车迎风面处于较大正压状态，由于两侧面的压差较大，有大量的漩涡产生和脱落，使得背风面处于高负压状态.空调导流罩和受电弓导流罩与车体相接处均呈现较大的正压，在拐角处产生较高负压，由此造成列车前后压差使列车承受的阻力增大；随着风向角的增大，空调导流罩和受电弓导流罩所受到的侧向力也逐步增大.

3.2.2 风向角为-24°时的速度矢量分布

列车头部在距地面1.8 m的水平横断面上的速度矢量分布见图7，列车尾部横剖面外轮廓周围速度矢量分布见图8.

图7表明，由于风向角的增大，造成列车表面压力、速度分布的不对称性.当气流经过鼻端继续沿车体流动时，车身表面的压力开始下降，表面压力最大处为迎风侧速度来流处.

图7 列车头部周围速度矢量分布

图8表明，列车在侧风环境下运行时，在列车背风侧，空气流动产生旋涡，故背风侧空气速度明显小于迎风侧速度.列车周围最大速度为114.11 m/s.由于转向架与车体之间空间较小，导致气流流动空间变小，气流方向发生改变，其中一部分气流进入车身下方转向架区域内，由于此处车体端墙区域周围相对封闭，导致转向架周围的气流无法及时导出，因此在转向架周围气流速度较小.

图8 列车尾部横剖面外轮廓周围速度矢量分布

3.2.3 风向角对气动性能的影响

高速列车在侧风环境中运行时，随着侧风风向角的变化，列车承受的阻力、侧向力均在不断变化.动车组在侧风环境中运行时，风速设定为60 m/s，列车各部分阻力系数和侧向力系数随风向角变化曲线见图9、图10.

图9(a)表明，随风向角的增大，头车所受阻力系数先增大后减小，这是由于车头形状为曲面，风向角为0°时，来流速度垂直于车头，有风向角时，来流速度并非完全垂直于车头，车头曲面处受到的力被分解为垂直来流速度方向的切向力和垂直车头曲面切线的力.随角度的增大，阻力逐渐增大，当角度增大到10°时，头车阻力系数达到最大，此时空调导流罩所受阻力占总头车阻力的3%，随着角度进一步增大，阻力逐渐减小.图9(b)表明，在-24°～24°范围内，中车的阻力系数随风向角增大逐渐增大，空调导流罩阻力系数曲线呈现先增大后减小的趋势，其阻力在无风环境下占据总的中车的4%，受电弓导流罩阻力系数曲线在此范围内呈现先减小后增大的趋势，在24°时占据总的中车阻力的14%，可看出在列车运行过程中，受电弓导流罩对列车中车所受阻力的影响较大.图9(c)表明，尾车的阻力系数曲线变化趋势与中车的变化趋势相同， 空调导流罩阻 力 系数曲线在-24°～24°范围内基本也成呈现先增大后减小的趋势，当阻力系数达到最大时，所受阻力占总的尾车阻力的2%.图9(d)表明，中车所受阻力最大，且由图9(b)可看出因受电弓导流罩的存在，导致中车承受的阻力较大，其阻力系数比风向角为0°时增大了97%，头车的阻力系数变化范围明显小于尾车，整车的阻力系数在方向角为12°时增大了68%，24°时增大了103%.

(a) 头车

(a) 头车

根据数据分析，对侧风风向角与列车气动阻力系数进行高斯曲线拟合，整车阻力系数的拟合曲线相关系数范围为0.974 29～0.983 93，高斯曲线表达式为：

Cx=C0+Ae(-0.5((x-xc)/w)2)

(1)

式中:C0=0.862 76；A=-0.408 54；xc=0.115 14；w=8.338 69;e取2.718 28.可计算出列车在不同风向角下的气动阻力系数.

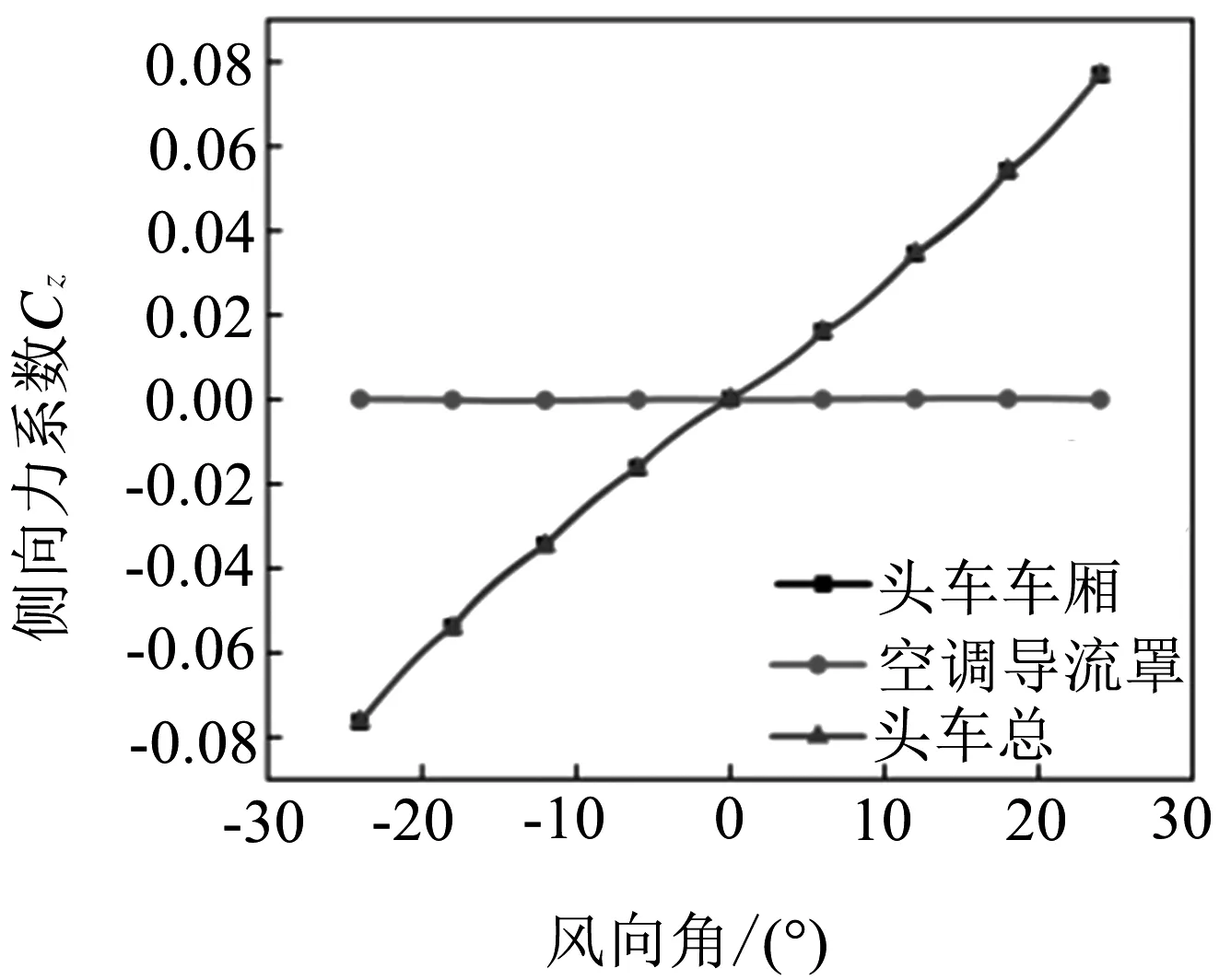
图10(a)、10(b)表明，在0°～±24°范围内，头车和中车侧向力系数绝对值均随风向角的增大而逐步增大，受电弓导流罩所受侧向力的绝对值随风向角增大而增大；风向角从0°变化为24°时，侧向力系数从6.24×10-5变化为0.001 6，增大了24倍；当风向角到达24°时其侧向力系数占总中车的4%，车顶空调导流罩受到的侧向力占总侧向力的3%.图10(c)表明，尾车的侧向力系数曲线走势呈波动状，原因为尾流区气流的不稳定性较大，随着角度的增大，迎风侧与背风侧的压差也在增大，尾流出现较多分离涡，导致尾车侧向力系数波动无规律.图10(d)表明，在0°～±24°范围内，头车所受到的侧向力最大，中车次之，尾车所受到的侧向力最小，且尾车侧向力系数受风向角变化的影响最小.风向角从0°变化为24°时，头车所受侧向力系数由9.4×10-5变化为0.076 9，增大了800倍，风向角为12°时整车侧向力系数增大了224倍，24°时增大了500倍.根据曲线走势，侧向力系数有持续增大的趋势，角度越大，列车越容易发生倾覆.而尾车在角度从0°变成24°时侧向力系数增大的幅值为4，数值较头车和中车而言始终最小，故尾车相对安全.

根据数据分析，对侧风风向角与列车侧向力系数进行三次函数曲线拟合，整车侧向力系数的拟合曲线相关系数范围为0.997 26～0.998 29，三次函数曲线表达式为：

Cz=A+Bx+Cx2+Dx3

(2)

式中：A=-0.001 37；B=0.003 83；C=4.632 24×10-6；D=2.202 78×10-6；x为侧风风向角.可计算出列车在不同风向角下的侧向力系数.

4 结论

(1)风向角在-12°～+12°范围内，车身部分测点表面压力系数的数值模拟结果和风洞试验结果误差范围控制在10%以内，因此验证了计算模型与计算方法的可行性.

(2)列车表面压力最大处为迎风侧速度来流处，且气流通过车头沿着车体表面向车身流动时，由于气流方向和速度的改变，在车头与车身连接处出现负压区；随风向角的增加，车头与车身连接处的负压程度增强，且列车表面压力、速度分布的不对称性增大，在列车迎风侧出现大面积正压区,背风面一侧的空气流动产生旋涡，出现较多的负压区，车体周围的速度也在逐渐增大；风向角从0°增大到9°，进一步增大到24°时，车体表面最大负压值从-3 500 Pa增大到-5 169 Pa，最后增大为-9 100 Pa.

(3) 整车阻力系数与风向角的关系曲线拟合方程满足高斯方程Cx=C0+Ae(-0.5((x-xc)/w)2)，整车阻力系数且随着风向角的增加而相应增大，受电弓导流罩使得中车承受更大的阻力系数，故中车所受到的气动阻力最大，尾车、头车次之，整车的阻力系数在方向角为12°时增加了68%，24°时增大了103%.

(4) 整车侧向力系数与风向角的关系曲线拟合方程满足三次函数方程Cz=A+Bx+Cx2+Dx3，整车侧向力系数的其绝对值随风向角的增大相应增大，头车所受到的侧向力系数最大，中车和尾车次之，风向角为12°时整车侧向力系数增大了224倍，风向角为24°时的整车侧向力系数为0.12，增大了500倍，因此在大风向角的环境中列车有更明显脱轨和倾覆的趋势，应多开展列车在大风向角侧风环境中的研究.