一类非齐次椭圆方程组非常弱解的正则性

陈淑红

一类非齐次椭圆方程组非常弱解的正则性

陈淑红

（武夷学院 数学与计算机学院，福建 武夷山 354300）

研究一类非齐次项是-Laplace算子的椭圆方程组非常弱解的正则性。结合Hodge分解以及偏微分方程正则性理论的证明技巧，建立了具有-Laplace型椭圆方程组的非常弱解与经典意义下的弱解之间的关系。

-Laplace型；非常弱解； Hodge分解；正则性

0　引言

考虑一类非齐次项具有-Laplace算子的椭圆方程组

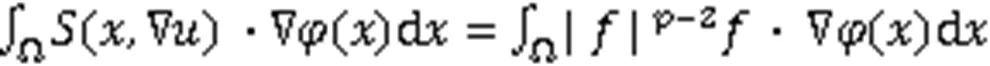
本文主要研究非齐次椭圆方程组（式（1））非常弱解的正则性。在著名数学家Hilbert于1904年提出的20个公开问题中，涉及解的正则性问题的就有2个，可见正则性研究的重要性，因此也吸引了研究者的广泛关注和探索，并取得了丰硕的成果［1-5］。

正则性理论的研究大多是在方程（组）存在弱解的情况下进行的，然而，很多具体形式、特定形式的方程（组）在已有研究方法下尚无法获得经典意义上的弱解，如具有奇异对流的方程组［6］、具有-Laplace型非齐次项的椭圆方程［7］等。

解的存在性仍然是一个悬而未决的问题。

幸运的是，1992年，IWANIEC［9］偶然发现在广义积分意义下，解的可积性指标在一定程度上可低于自然增长指标，由此提出了在经典意义下的弱解，即在更广泛的空间内定义方程弱解，并将其定义为非常弱解。

1　基本引理

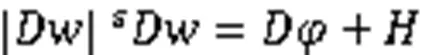
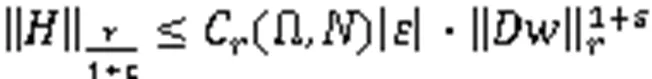
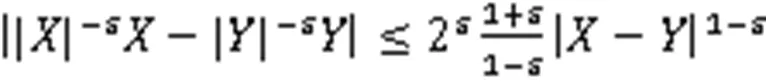
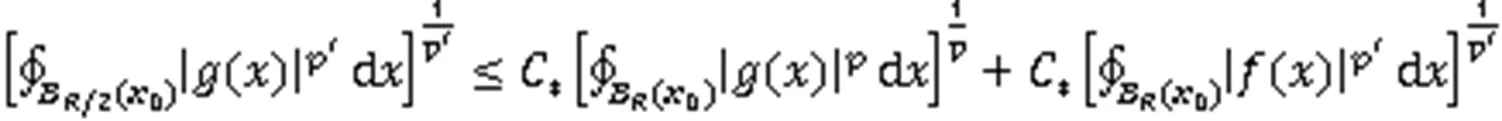
2　正则性证明

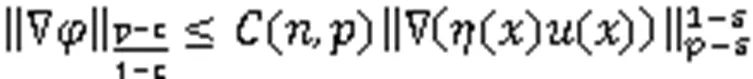
令

由引理3，可得

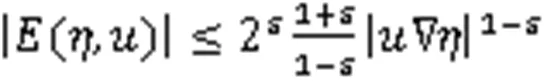
由式（9）和式（11），可推得

代入式（13），得

由式（2）和式（3），得

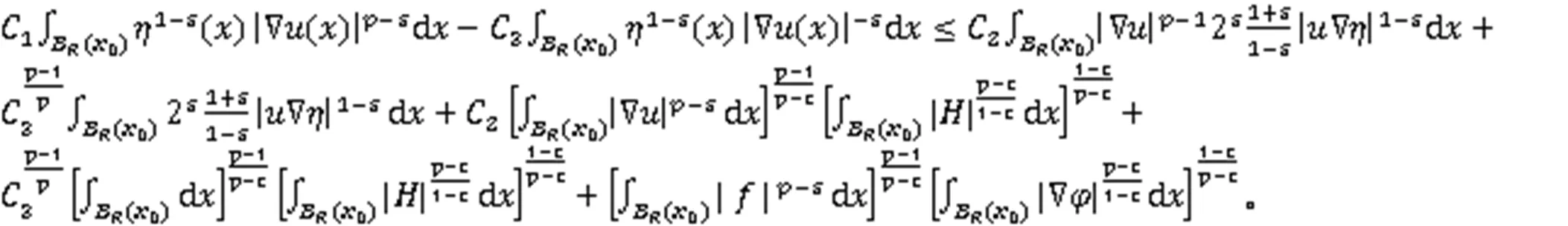
由引理2和等式（10），可以发现

其中，

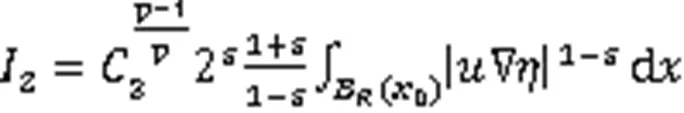
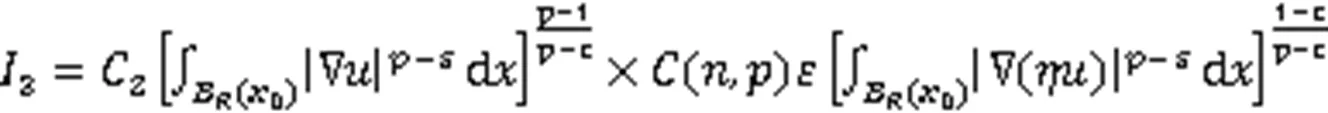
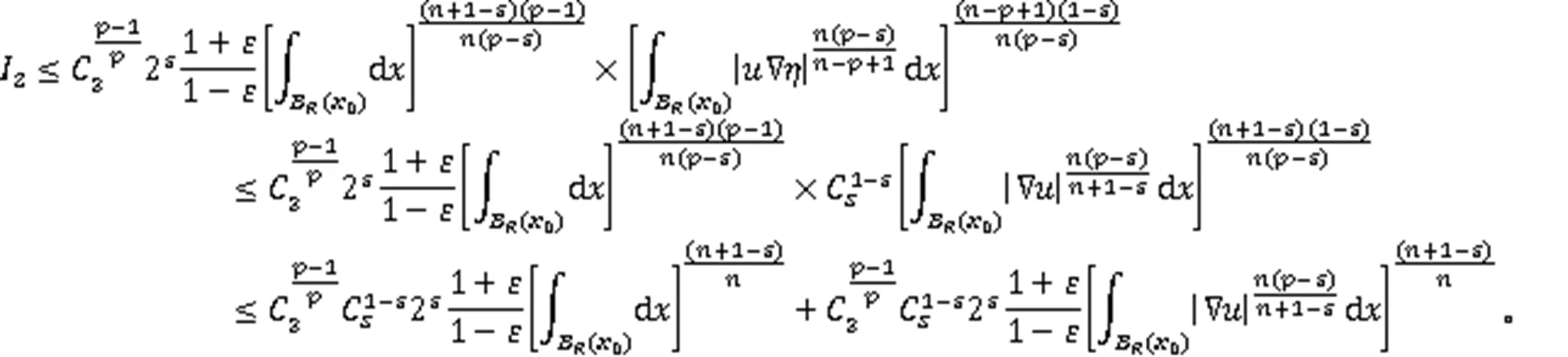
由式（10）、Young不等式以及Poincare不等式，有

再利用Young不等式和Poincare不等式，可得

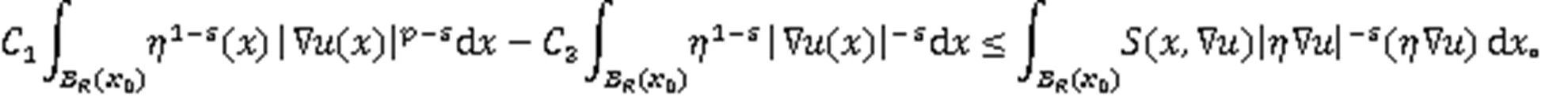
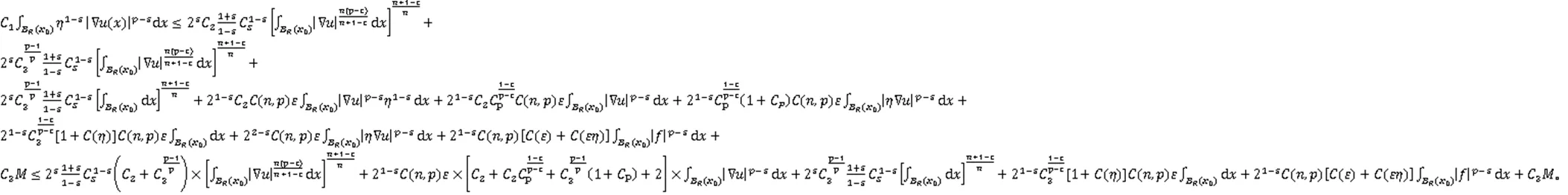
重复上述过程，则由引理4，可得定理1成立。

推论1获证。

［1］ BECK L. Partial regularity for weak solutions of nonlinear elliptic systems： The subquadratic case［J］. Manuscripta Mathematica， 2007， 123： 453-491. DOI：10.1007/s00229-007-0100-8

［2］ ARAMAKI J. Regularity of weak solutions for degenerate quasilinear elliptic equations involving operator curl［J］. Journal of Mathematical Analysis and Applications， 2015， 426（2）： 872-892. DOI：10. 1016/J.JMAA.2015.02.001

［3］ LIU Q. Regularity of weak solutions and the number of singular points to the 3D simplified nematic liquid crystal system［J］. Journal of Functional Analysis， 2019， 277（12）， 108294.

［4］ OK J. Partial Hölder regularity for elliptic systems with non-standard growth［J］. Journal of Functional Analysis， 2018， 274（3）： 723-768. DOI：10.1016/j.jfa.2017.11.014

［5］ KIM H. Existence and regularity of very weak solutions of the stationary Navier-Stokes equations［J］. Archive for Rational Mechanics and Analysis， 2009， 193（1）： 117-152. DOI：10.1007/s00205-008-0168-7

［6］ GRECO L， MOSCARIELLO G， ZECCA G， et al. Very weak solutions to elliptic equations with singular convection term［J］. Journal of Mathematical Analysis and Applications， 2018， 457（2）： 1376-1387. DOI：10.1016/j.jmaa.2017.03.025

［7］ BULÍČEK M， SCHWARZACHER S. Existence of very weak solutions to elliptic systems of-Laplacian type［J］. Calculus of Variations and Partial Differential Equations， 2016， 55（52）. DOI：10. 1007/s00526-016-0986-7

［8］ BÉNILAN P， BOCCARDO L， GALLOUËT T， et al. An1-theory of existence and uniqueness of solutions of nonlinear elliptic equations［J］. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze， 1995， 22（2）： 241-273.

［9］ IWANIEC T.-harmonic tensors and quasiregular mappings［J］. Annals of Mathematics， 1992， 136（3）： 589-624. DOI：10.2307/2946602

［10］IWANIEC T， SBORDONE C. Weak minima of variational integrals［J］. Journal für die Reine und Angewandte Mathematik， 1994， 454： 143-161. DOI：10.1515/crll.1994.454.143

［11］IWANIEC T， MIGLIACCIO L， NANIA L. Integrability and removability results for quasiregular mappings in high dimensions［J］. Mathematica Scandinavica， 1994， 75（2）： 263-279. DOI：10.7146/MATH.SCAND.A-12519

［12］MEYERS N， ELCRAT A. Some results on regularity for solutions of non-linear elliptic systems and quasi-regular functions［J］. Duke Mathematical Journal， 1975， 42（1）： 121-136. DOI：10.1215/S0012-7094-75-04211-8

Regularity of very weak solutions for a class of inhomogeneous elliptic equations

CHEN Shuhong

（，，354300，，）

In this paper, we study the regularity theory of very weak solutions for a class of elliptic equations which inhomogeneous terms are-Laplace operators. Combining Hodge decomposition and the regularity theory of partial differential equations, the relation between the very weak solution of-Laplacian elliptic equations and the weak solution in the classical sense is established.

-Laplace type; very weak solution; Hodge decomposition; regularity

O 175.2

A

1008⁃9497（2023）01⁃025⁃05

2021⁃09⁃09.

国家自然科学基金资助项目（11571159）；武夷学院引进人才科研启动项目（YJ202118）.

陈淑红（1979—），ORCID：https：//orcid.org/0000-0001-6648-6486，女，博士（后），教授，主要从事偏微分方程研究，E-mail：shiny0320@163.com.