空间参数曲线的双目标能量极小化方法及其应用
2023-01-17李军成刘成志罗志军龙志文
李军成,刘成志,罗志军,龙志文
空间参数曲线的双目标能量极小化方法及其应用
李军成,刘成志,罗志军,龙志文
(湖南人文科技学院 数学与金融学院,湖南 娄底 417000)
能量极小化方法已广泛用于平面曲线的构造,而在空间曲线构造方面的应用尚少。首先介绍了空间参数曲线的弯曲能和扭曲能,然后提出了一种以弯曲能和扭曲能同时极小为目标的空间参数曲线构造方法,最后以空间三次Bézier曲线为例,探讨了该方法在曲线的构造、延拓、平滑等问题中的应用。所提出的方法更符合空间参数曲线既需考虑弯曲又需考虑扭曲的特点。
空间参数曲线;能量极小化;弯曲能;扭曲能;双目标优化; Bézier曲线
在几何设计与计算中,如何利用能量极小化方法构造曲线、曲面广受关注。近年来,已有许多针对此问题开展的研究,例如,利用能量极小化方法构造B样条曲线[1-2]、Bézier曲线[3-5]、插值曲线和曲面[6-9],进行Hermite插值[10-16]以及生成曲面网格[17-18]等。
在利用能量极小化方法构造曲线时,大多以平面曲线为研究对象,对空间曲线的构造研究较欠缺。文献[19]给出了空间曲线弯曲能和扭曲能的定义,并讨论了弯曲能极小和扭曲能极小的情况。通常,平面曲线仅需考虑弯曲,空间曲线则既需考虑弯曲又需考虑扭曲,因此,在利用能量极小化方法构造空间曲线时,应同时考虑弯曲能和扭曲能。遗憾的是,目前鲜有文献讨论如何利用弯曲能和扭曲能同时极小化构造空间曲线。
首先介绍空间参数曲线的弯曲能和扭曲能,然后给出一种用于构造空间参数曲线的双目标能量极小化方法,最后以空间三次Bézier曲线为例,给出双目标能量极小化方法在空间三次Bézier曲线构造中的应用。
1 空间参数曲线的能量
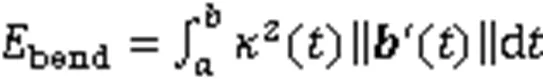
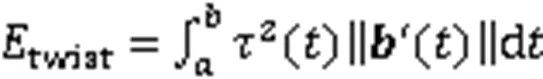
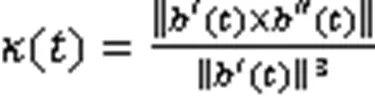
为简化计算,式(1)和式(2)可近似表示为[19]:

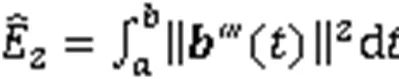
分别称为空间参数曲线的近似弯曲能和近似扭曲能。需要说明的是,式(3)在文献[2-3,7,10]中为平面参数曲线的近似弯曲能(又称应变能),式(4)在文献[2-3,5,13,15]中为平面参数曲线的近似曲率变化能(又称Jerk能)。
2 双目标能量极小化方法




通常可将式(5)转化为单目标优化问题:
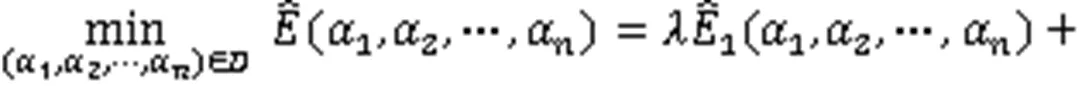
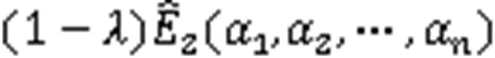

Step 1 计算2个单目标之间的偏差:
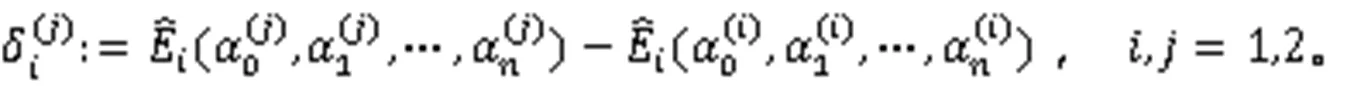
Step 2 计算2个单目标的偏差之和:
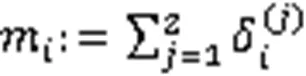
Step 3 计算2个单目标的初始权重:
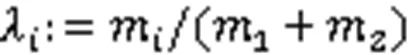
最后,利用相应优化方法求得式(6)的最优解,得到式(5)的非劣解。
3 应用
空间三次Bézier曲线可表示为[21]
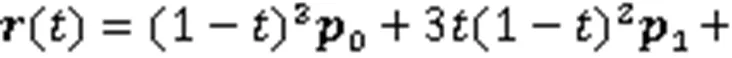
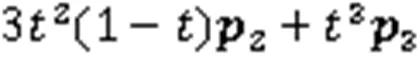
3.1 空间三次Bézier曲线的构造
Bézier曲线是一种重要的几何造型工具,广泛应用于工业设计领域。在构造Bézier曲线时,需施加一定的几何或物理约束,使得所构造曲线满足相应要求。其中约束类型众多,能量约束已成为构造光顺曲线的一种常用方式。例如,文献[3,5]给出了利用能量极小化构造Bézier曲线的方法。用能量极小化构造三次Bézier曲线时,除给定首、末控制顶点外,还需给定第3个控制顶点,才能确定第4个控制顶点,从而构造具有极小能量的三次Bézier曲线。然而,若利用文献[3,5]中的方法构造三次Bézier曲线,无论是应变能极小还是Jerk能极小,均仅考虑了曲线的弯曲或扭曲。
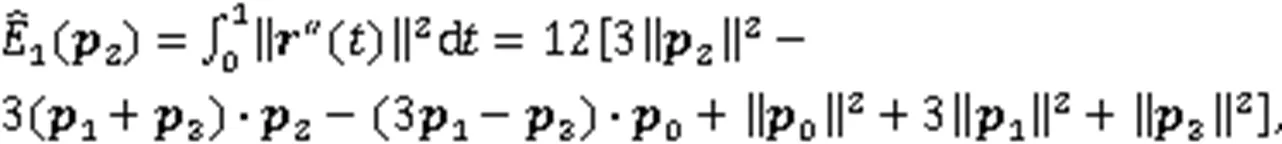
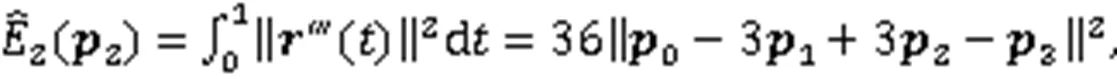
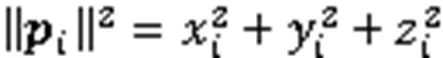
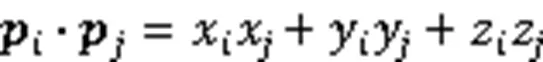
于是,由式(6)可得优化问题:


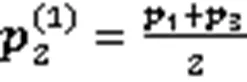

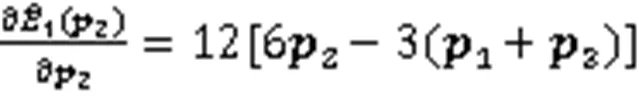
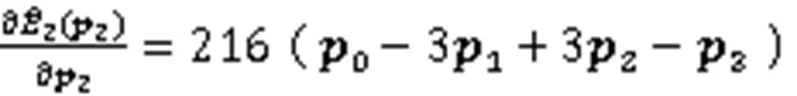
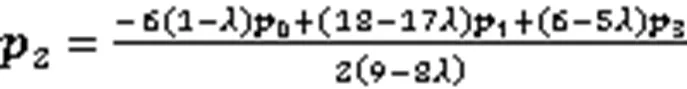
证明由式(11)可得

(i)若仅考虑弯曲能极小,则
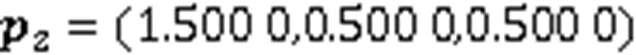
(ii)若仅考虑扭曲能极小,则

(iii)若同时考虑弯曲能和扭曲能极小(双目标能量极小),则
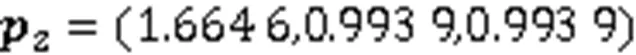
采用3种能量极小化方法构造的空间三次Bézier曲线如图1所示,计算所得的弯曲能、扭曲能如表1所示。可知,采用双目标能量极小化方法所构造曲线的弯曲能和扭曲能介于另2种方法之间,这符合空间参数曲线既需考虑弯曲又需考虑扭曲的特点。
图1 3种能量极小化方法构造的空间三次Bézier曲线
Fig.1 Spatial cubic Bézier curves constructed by three energy minimizations
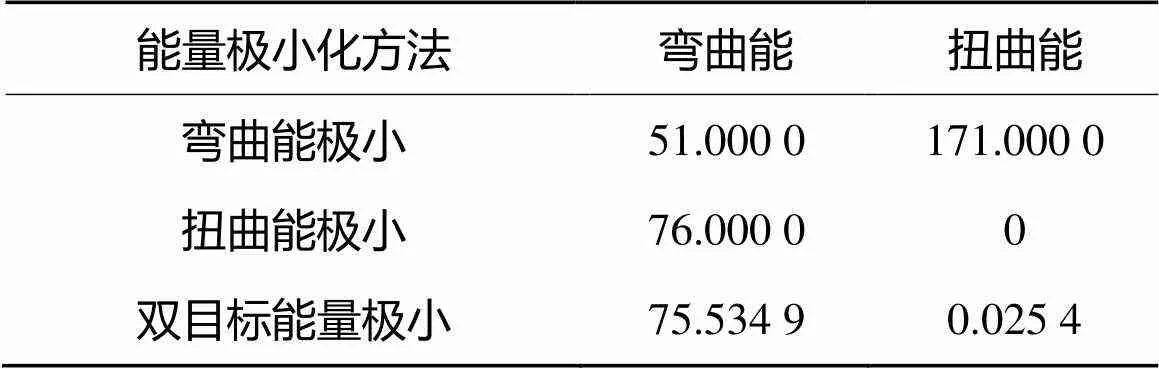
表1 3种能量极小化方法的弯曲能和扭曲能
3.2 空间三次Bézier曲线的延拓
在计算机辅助设计系统中,为满足复杂曲线的造型需要,将一条已知的Bézier曲线延拓至给定的点,延拓曲线亦用Bézier曲线表示,并与原曲线在连接点处满足一定的连续性条件。
不妨设曲线

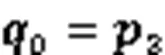
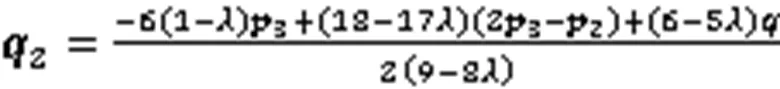

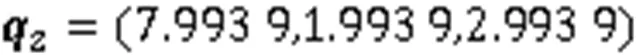
空间三次Bézier曲线的延拓如图2所示。
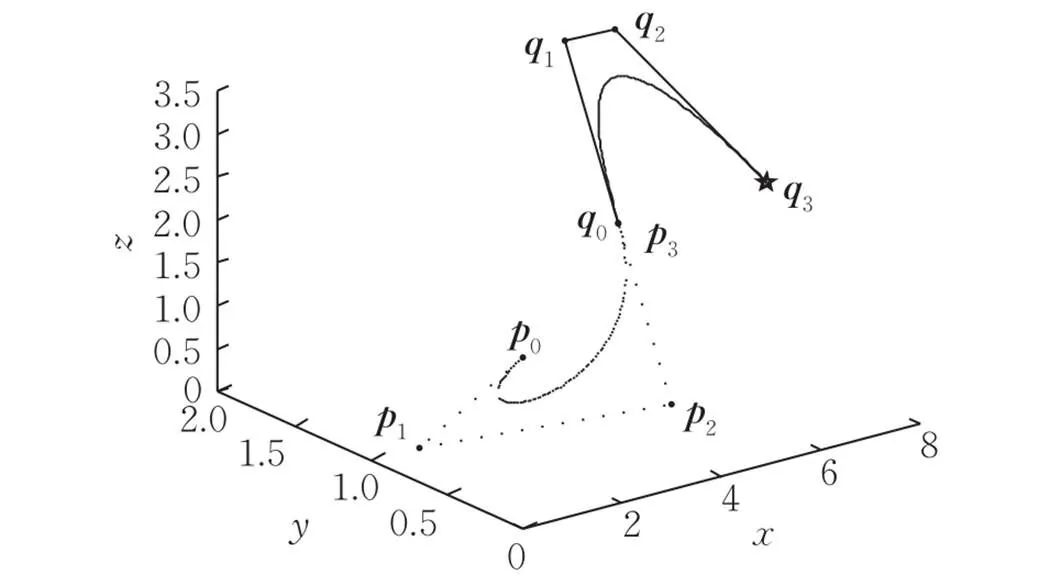
图2 空间三次Bézier曲线的延拓
3.3 空间链接曲线的平滑
在利用空间三次Bézier曲线进行复杂几何造型时,需链接多条空间三次Bézier曲线,当空间链接曲线的连续性较低时,需通过调整控制顶点提高其连续性。
给定2条空间三次Bézier曲线:

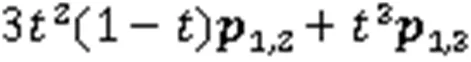

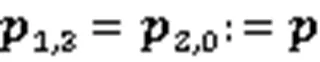
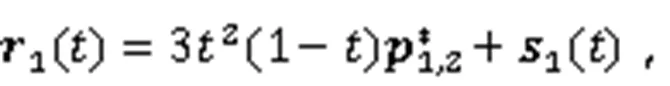

其中,

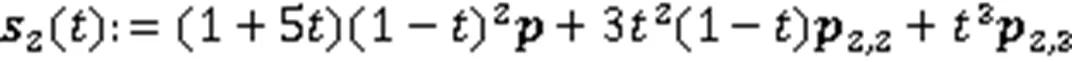
由式(3)、式(4)、式(23)和式(24),经平滑处理后2条曲线的总弯曲能函数和总扭曲能函数分别为:
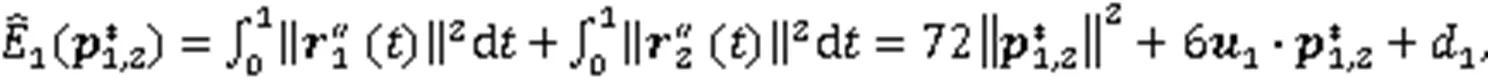

其中,

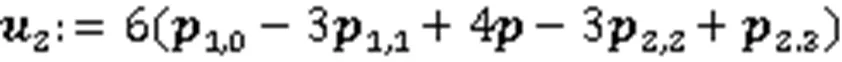
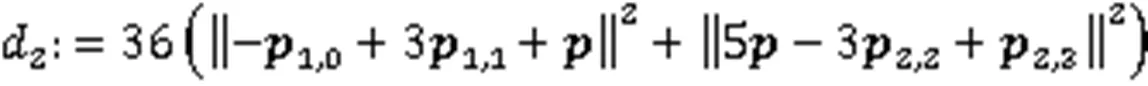
于是,由式(6)可得双目标能量优化问题:
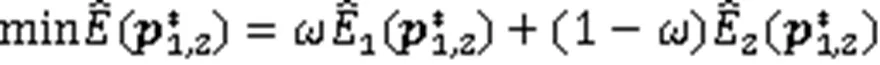
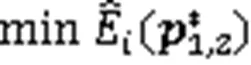
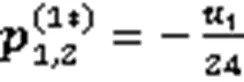
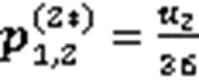
证明由式(25)可得
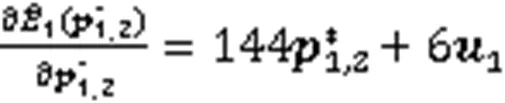
由式(26)可得
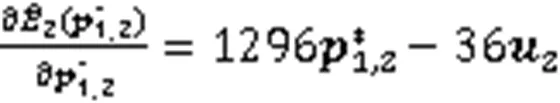
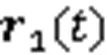
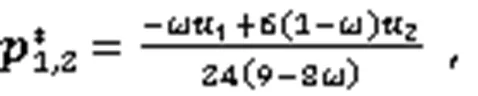
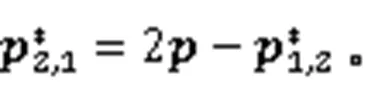
证明由式(27),可得
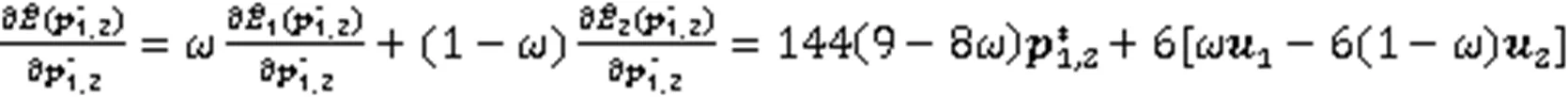

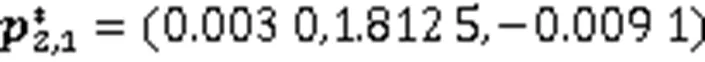
0连续链接曲线与平滑后的1连续链接曲线如图3所示。

图3 空间链接曲线的平滑
4 结语
针对如何利用能量极小化方法构造空间参数曲线的问题,提出了一种双目标能量极小化方法,探讨了该方法在构造空间三次Bézier曲线及其延拓和平滑等问题中的应用。因双目标能量极小化方法同时考虑了弯曲能和扭曲能,其较仅考虑弯曲能极小或扭曲能极小的方法更符合空间参数曲线的特点。研究为利用能量极小化方法构造空间参数曲线提供了一种有效的手段。
[1] VASSILEV T I. Fair interpolation and approximation of B-splines by energy minimization and points insertion[J]. Computer-Aided Design, 1996, 28(9): 753-760. DOI:10.1016/0010-4485(95)00087-9
[2] XU G, ZHU Y F, DENG L S, et al. Efficient construction of B-spline curves with minimal internal energy[J]. Computers, Materials & Continua, 2019, 58(3): 879-892. DOI:10.32604/cmc.2019.03752
[3] XU G, WANG G Z, CHEN W Y. Geometric construction of energy-minimizing Bézier curves[J]. SCIENCE CHINA Information Sciences, 2011, 54(7): 1395-1406. DOI:10.1007/s11432-011-4294-8
[4] AHN Y J, HOFFMANN C, ROSEN P. Geometric constraints on quadratic Bézier curves using minimal length and energy[J]. Journal of Computational and Applied Mathematics, 2014, 255: 887-897. DOI:10. 5555/2753878.2754090
[5] ERİŞKİN H, YÜCESAN A. Bézier curve with a minimal Jerk energy[J]. Mathematical Sciences and Applications E-Notes, 2016, 4(2): 139-148. DOI:10.36753/MATHENOT.421467
[6] ZHANG C M, ZHANG P F, CHENG F H. Fairing spline curves and surfaces by minimizing energy[J]. Computer-Aided Design, 2001, 33(13): 913-923. DOI:10.1016/S0010-4485(00)00114-7
[7] YONG J H, CHENG F H. Geometric Hermite curves with minimum strain energy[J]. Computer Aided Geometric Design, 2004, 21(3): 281-301. DOI:10.1016/j.cagd.2003.08.003
[8] LI J C, LIU C Z, ZHANG L. Shape-preserving planar quadratic Bézier interpolation spline with minimal stretch energy[J]. Journal of Testing and Evaluation, 2020, 48(3): 2432-2440. DOI:10.1520/JTE20190809
[9] 李军成,刘成志,赵文才. 优化端点条件的平面二次均匀B样条插值曲线[J]. 浙江大学学报(理学版), 2021, 48(2): 159-166. DOI:10.3785/j.issn.1008-9497.2021.02.004
LI J C, LIU C Z, ZHAO W C. Planar quadratic uniform B-spline interpolation curve with optimized endpoint condition[J]. Journal of Zhejiang University (Science Edition), 2021, 48(2): 159-166. DOI:10.3785/j.issn.1008-9497.2021.02.004
[10]JAKLIČ G, ŽAGAR E. Planar cubic1interpolatory splines with small strain energy[J]. Journal of Computational and Applied Mathematics, 2011, 235(8): 2758-2765. DOI:10.1016/j.cam.2010.11.025
[11]JAKLIČ G, ŽAGAR E. Curvature variation minimizing cubic Hermite interpolants[J]. Applied Mathematics and Computation, 2011, 218(7): 3918-3924. DOI:10.1016/j.amc.2011.09.039
[12]LU L Z. Planar quintic2Hermite interpolation with minimum strain energy[J]. Journal of Computational and Applied Mathematics, 2015, 274: 109-117. DOI:10.1016/j.cam.2014.07.015
[13]LU L Z. A note on curvature variation minimizing cubic Hermite interpolants[J]. Applied Mathematics and Computation, 2015, 259: 596-599. DOI:10. 1016/j.amc.2014.11.113
[14]LU L Z, JIANG C K, HU Q Q. Planar cubic1and quintic2Hermite interpolations via curvature variation minimization[J]. Computers & Graphics, 2018, 70: 92-98. DOI:10.1016/j.cag.2017.07.007
[15]LI J C, ZHANG L. Length and curvature variation energy minimizing planar cubic1Hermite interpolation curve[J]. Journal of Taibah University for Science, 2019, 14(1): 60-64. DOI:10.1080/16583655.2019.1703248
[16]LI J C. Combined internal energy minimizing planar cubic Hermite curve[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2020, 14(7): 20-00308. DOI:10.1299/jamdsm.2020jamdsm0103
[17]BOCK K, STILLER J. Energy-minimizing curve fitting for high-order surfaces mesh generation[J]. Applied Mathematics, 2014, 5: 3318-3327. DOI:10.4236/am.2014.521309
[18]BOCK K, STILLER J. Optimizing triangular high-order surface meshes by energy-minimization[J]. Engineering with Computers, 2018, 34(4): 659-670. DOI:10.1007/s00366-017-0565-3
[19]VELTKAMP R C, WESSELINK W. Modeling 3D curves of minimal energy[J]. Computer Graphics Forum, 1995, 14(3): 97-110. DOI:10.1111/j.1467-8659.1995.cgf143_0097.x
[20]林锉云,董加礼. 多目标优化的方法与理论[M]. 长春:吉林教育出版社, 1992.
LIN C Y, DONG J L. The Methods and Theories of Multi-Objective Optimizations[M]. Changchun: Jilin Education Press, 1992.
[21]FARIN G. Curves and Surfaces for CAGD: A Practical Guide[M]. San Diego: Academic Press, 2002.
Bi-objective energy minimization of spatial parametric curves and its applications
LI Juncheng, LIU Chengzhi, LUO Zhijun, LONG Zhiwen
(,,,417000,,)
Although approach of energy minimizations has been widely applied in the construction of planar curves, it is seldom used in the construction of spatial curves. In this paper, we first introduce the bending energy and twisting energy of spatial parametric curves. A method of constructing spatial parametric curves aiming at minimizing the bending energy and twisting energy simultaneously is then proposed. Finally, the applications of the proposed method in the construction, extension, and smoothing of the cubic Bézier curve are discussed. The proposed method conforms with the fact that both bending and twisting are important shape features of spatial parametric curves.
spatial parametric curve; energy minimization; bending energy; twisting energy; bi-objective optimization; Bézier curve
TP 391.72
A
1008⁃9497(2023)01⁃063⁃06
2021⁃09⁃10.
湖南省自然科学基金资助项目(2021JJ30373);国家自然科学基金资助项目(12101225).
李军成(1982—),ORCID:https://orcid.org/0000-0002-1904-4068,男,博士,教授,主要从事计算机辅助几何设计及其应用研究,E-mail:lijuncheng82@126.com.
