三维非牛顿流体充填过程的有限元-间断有限元数值模拟研究

高普阳

三维非牛顿流体充填过程的有限元-间断有限元数值模拟研究

高普阳

（长安大学 理学院，陕西 西安 710064）

针对三维非牛顿流体充填问题，建立了有限元-间断有限元耦合算法。对于两相Navier-Stokes方程，基于压力增量修正格式分三步求解，分别采用二次和一次拉格朗日插值多项式求解速度和压力，以确保计算过程稳定。采用守恒型水平集（level set）方法追踪运动界面，并依据间断有限元方法求解水平集和重新初始化方程。以三维圆球剪切流动及非牛顿流体三维平板型腔充填过程为例，并与已有文献的数值和实验结果进行比较，以验证数值算法的稳定性、准确性以及流体的质量守恒性。

有限元；间断有限元；水平集；非牛顿充填过程

0　引言

非牛顿流体充填过程中涉及两种不同类型流体以及液体之间的运动界面，在三维情形下进行数值模拟，一直是关注的热点和难点［1-7］。数值模拟的关键是精确求解由两种流体构成流场信息、准确捕捉运动界面以及保证流体质量守恒性。

TOMÉ等［8］采用有限差分法求解流场控制方程、用VOF法追踪运动界面，并基于CFD Freeflow3D程序数值模拟了三维容器内非牛顿流体的充填过程，研究了入口速度对充填过程中自由界面形态及裹气现象的影响，并将数值结果与实验结果进行了对比。MUKRAS等［9］用ANSYS-CFX数值模拟了三维型腔内高密度聚乙烯的充填过程，分析了不同注射速度条件下的充填模式。LIU等［10-11］数值模拟了三维型腔内黏性非牛顿流体的共注射成型过程，对一些特有的流动现象进行了研究。ZHUANG等［12］基于有限体积法，用水平集方法追踪运动界面，数值模拟了三维型腔的充填过程，并分析了温度、黏弹性应力等对流动性态的影响。HE等［13］用光滑粒子动力学方法（SPH）模拟了幂律型非牛顿流体的充填过程，并分析了流动过程中前沿界面的形态以及纤维的取向。BORZENKO等［14］用SIMPLE算法求解流场控制方程，用VOF方法追踪运动界面，研究了三维矩形腔的非牛顿流体充填过程，分析了数和数等参数对自由界面的影响机理。目前尚鲜见相关用有限元-间断有限元方法模拟三维充填过程研究的报道，且充填过程大多未考虑流体的质量守恒性。

本文构建了三维充填过程的统一计算模型，并采用有限元-间断有限元耦合算法对模型进行数值模拟。首先，采用压力增量修正算法对统一计算模型进行分裂；然后，基于有限元法对其进行数值求解，对速度和压力分别取二次和一次拉格朗日插值基函数，以保证计算过程稳定；最后，为准确追踪运动界面并保证流体较好的质量守恒性，用守恒型水平集方法追踪运动界面，并用间断有限元法数值求解水平集及重新初始化方程。

1　数学模型

非牛顿流体充填过程属于非牛顿-牛顿两相流动问题，其数学模型主要包括流场控制方程和界面演化方程。

1.1　水平集方程

用守恒型水平集方法追踪两相流动的自由界面。用水平集函数（）的零等值面表示两流体间的运动界面，流场中某个点到界面的距离用函数（）的绝对值表示：

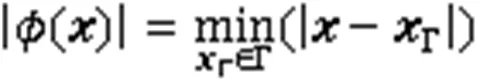
（）在空气区域内取正值，在液体区域内取负值。

在速度场影响下，自由界面的形态和位置发生变化，运动界面的水平集函数为

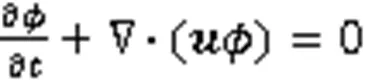
为确保界面附近水平集函数的符号距离特性和流体的质量守恒性，引入了修正型水平集，重新初始化方程［15］：

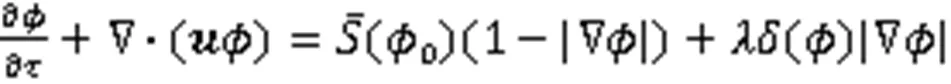
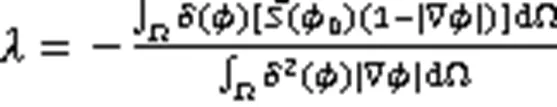
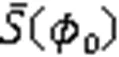
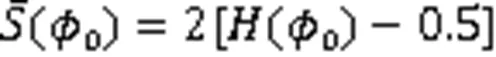
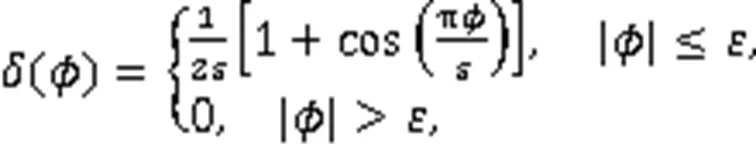
其中，（）为光滑的Heaviside函数，

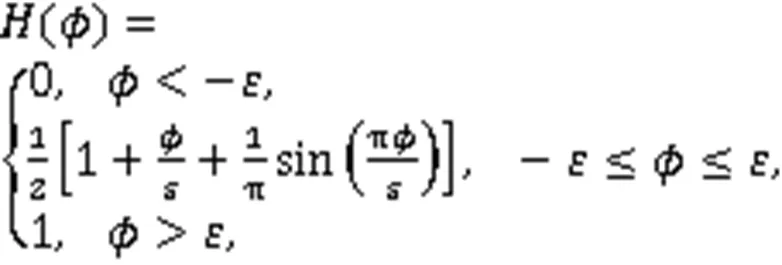
1.2　Navier-Stokes方程

非牛顿流体充填过程属于非牛顿-牛顿两相流动问题，流动过程涉及两种不同特性的流体。为方便计算，用统一形式：

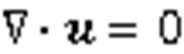
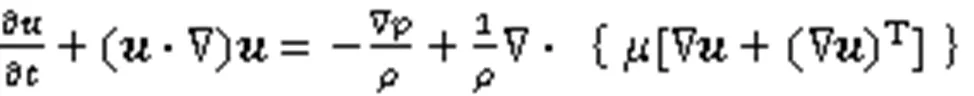
其中，=（，，）表示三维速度矢量，为压力。和分别为流动区域内的密度和黏度，

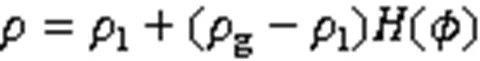
不同于牛顿流体，非牛顿流体的黏度受形变速率影响。本文用幂律型本构方程［16］描述黏度与形变速率张量之间的非线性关系：

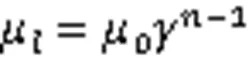
2　数值算法

2.1　统一形式Navier-Stokes方程的求解

用基于有限元的压力增量修正格式［17］对统一形式的Navier-Stokes方程进行数值求解。首先，引入中间速度*，对式（8）左端的时间项进行空间离散，显式处理压力项，对非线性对流项做线性化处理，式（8）右端的速度选用中间时刻的值：

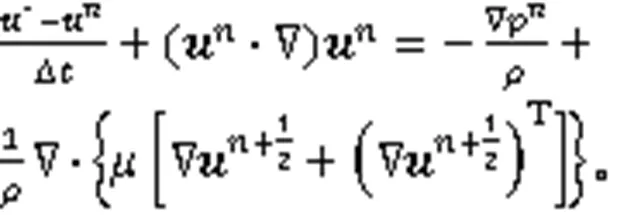
由中间速度*计算下一时刻的压力，半离散格式为

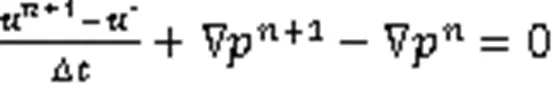
对式（10）和式（11）两边取散度，由速度+1的不可压缩条件，可得

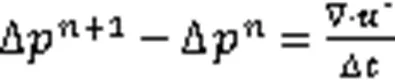
在进行空间离散前，需对求解区域Ω进行三角剖分，得到Ω，用Ω（=1，2，…，）表示三角网格上的小三角形。为保证计算过程稳定，需分别对速度和压力采用二次和一次多项式插值。定义2个有限元空间：

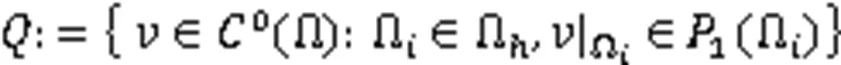
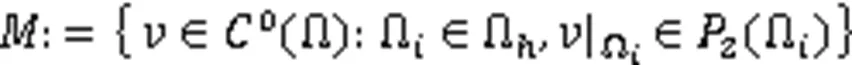
式（10）～式（12）的空间离散格式分别为

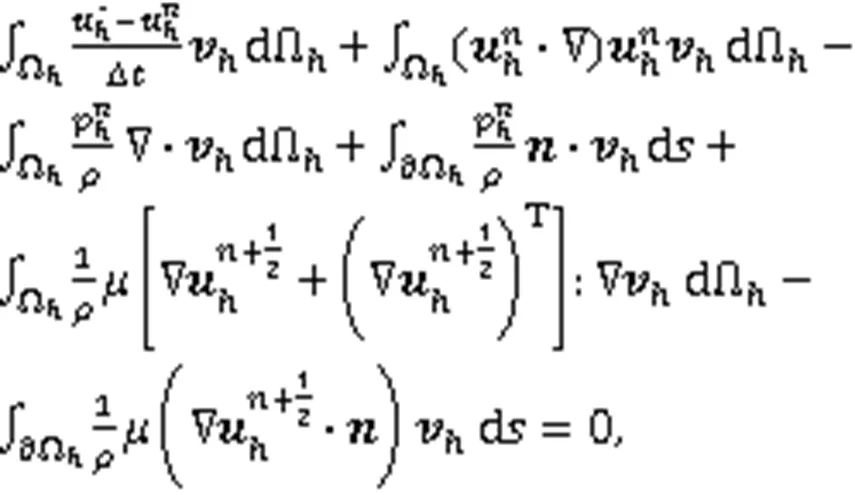
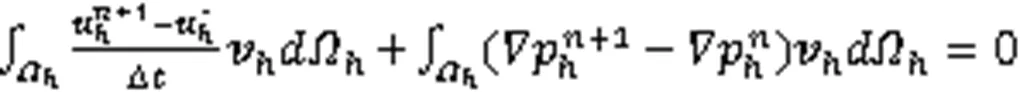
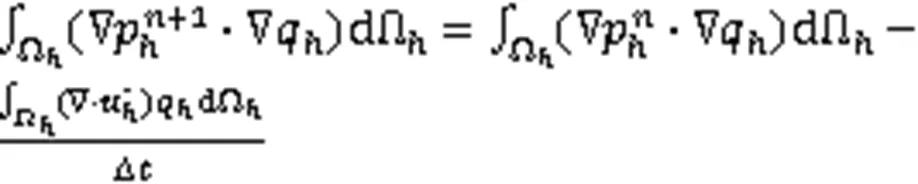
2.2　水平集方程的求解

在得到速度场之后，需要进一步求解水平集方程，以更新运动界面。水平集方程为双曲型方程，本文采用间断有限元方法进行数值求解。首先，将水平集方程（式（1））在时间上进行隐式离散，得到半离散方程

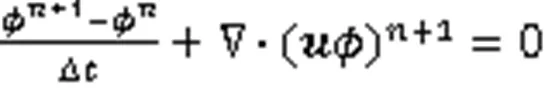
定义间断有限元空间

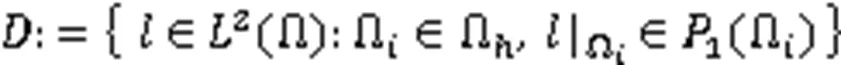
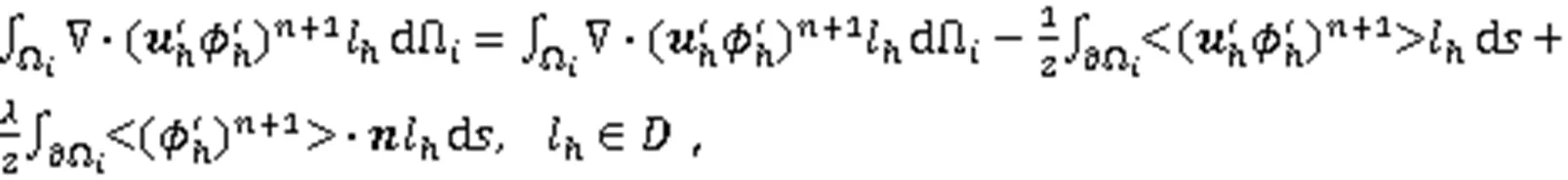
因此，式（16）的全离散格式为

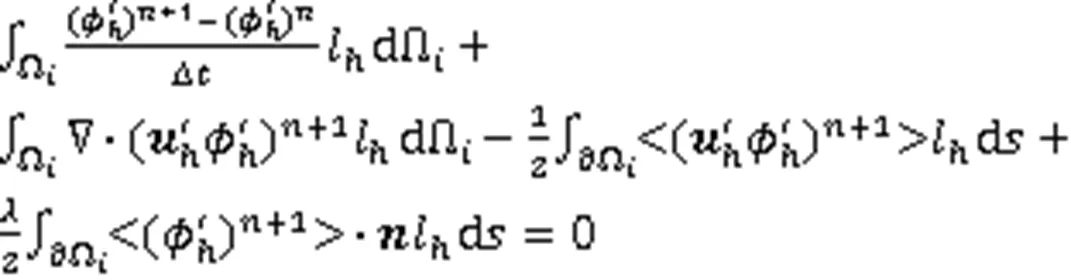
同理，水平集重新初始化方程的全离散格式为

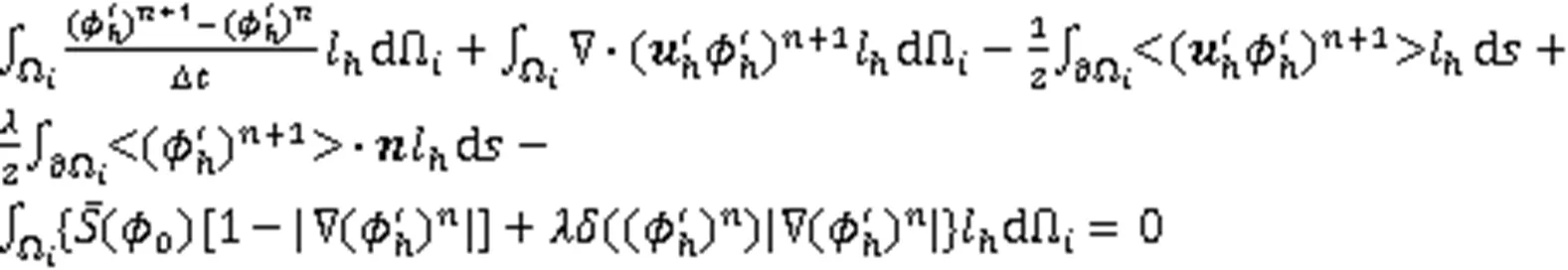
2.3　算法流程

算法流程如图1所示。

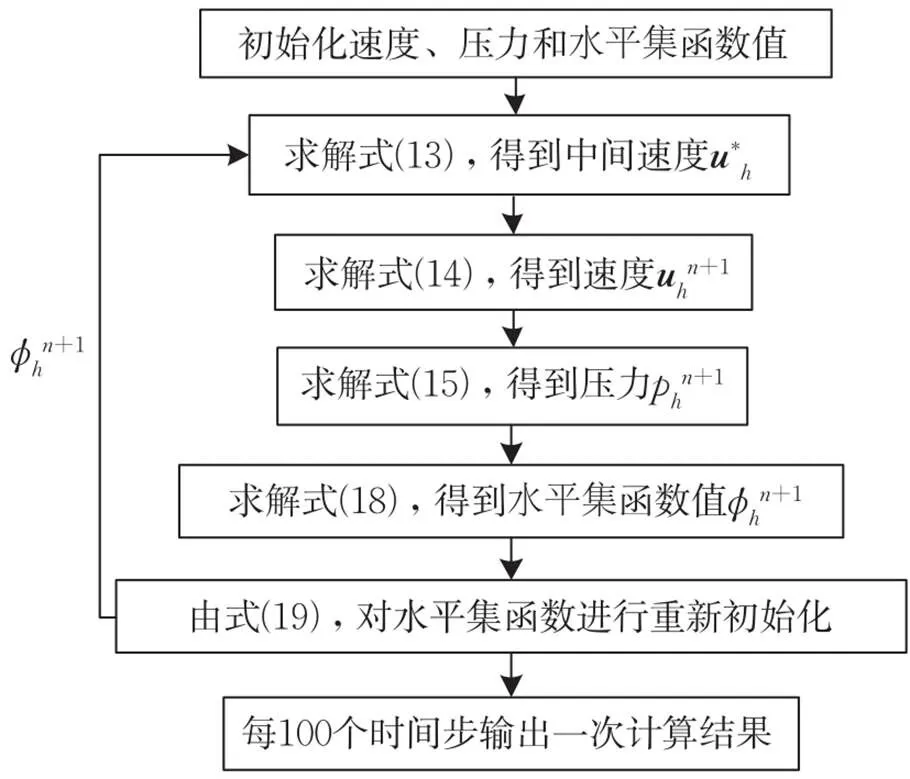
图1　算法流程

3　数值算例

3.1　三维圆球剪切流动

主要研究三维情形下的圆球剪切流动［18-19］，以验证数值算法在处理大变形自由界面问题时的稳定性、准确性和质量守恒性。假设初始状态下流场中圆球的球心坐标为（0.35，0.35，0.35），半径为0.15，如图2所示。流场内的速度为

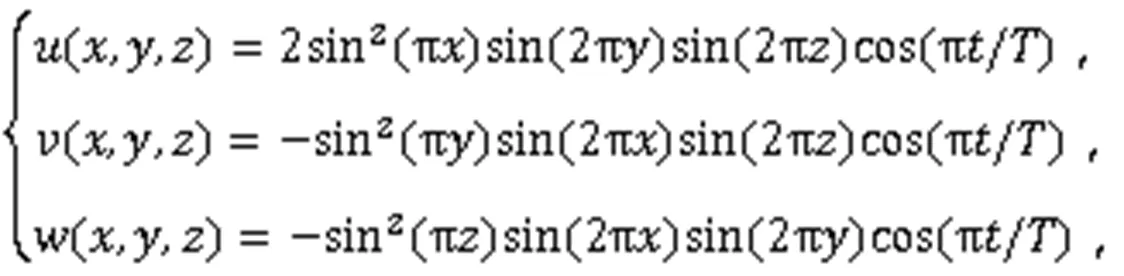
图3　当t =3.0时不同网格的自由界面形态

图4　不同时刻的自由界面形态

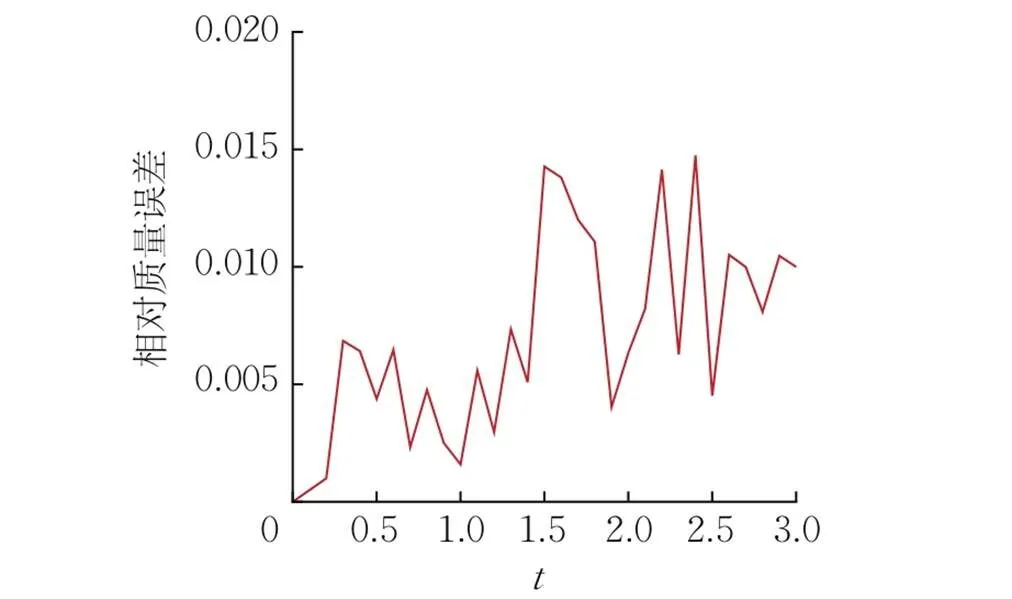
图5　网格3上相对质量误差随时间的变化

3.2　非牛顿流体三维平板型腔充填过程

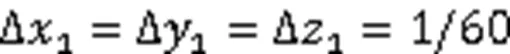
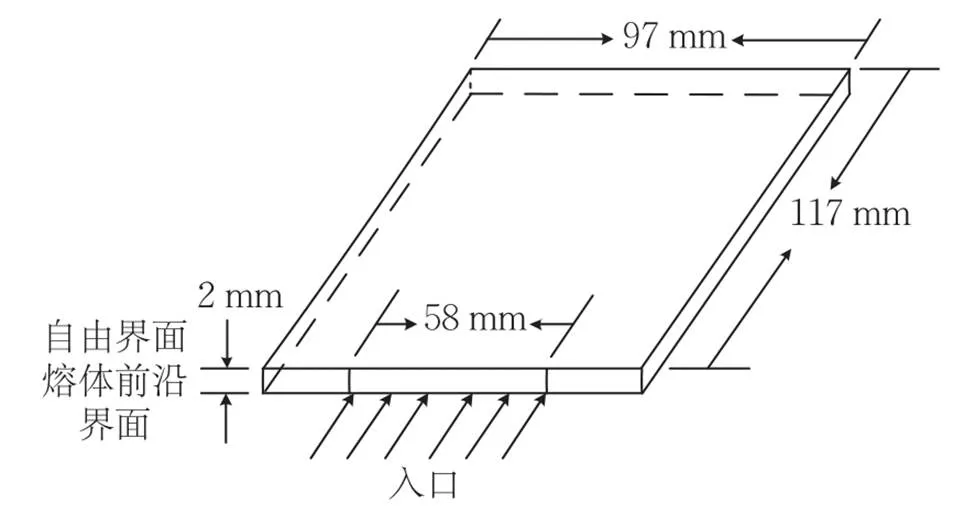
图6　三维型腔示意

图7　计算网格3示意

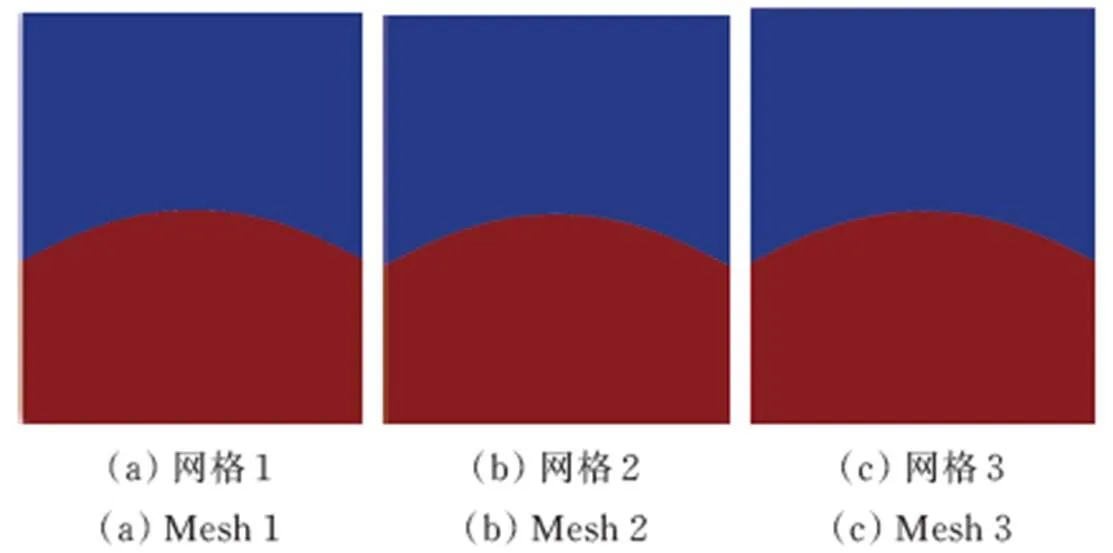
图8　当t =1.9 s时不同网格的熔体前沿界面形态

图9给出了不同时刻非牛顿流体前沿界面形态的实验结果、文献［9］的数值结果和本文的数值结果。可知，初始阶段液体前沿界面呈圆弧状，随着时间的推进，液体前沿界面的弧度逐渐变小，本文方法的数值结果和实验结果［9］吻合较好。图9中，（a）1.1 s，（b）1.9 s，（c）2.7 s，（d）3.5 s，（e）4.3 s分别对应液体区域所占型腔体积20%，40%，60%，80%和100%时的情形。网格1、网格2和网格3计算得到的熔体质量的最大相对误差分别为2.20%，1.00%和0.67%。数值结果表明，耦合算法能较稳定、准确地求解三维非牛顿流体的充填过程，并保证非牛顿流体具有较好的质量守恒性。随着充填过程的进行，型腔内熔体的总质量逐渐增加，图10给出了网格3熔体质量数值结果和精确结果之间的相对误差随时间的变化。图11进一步展示了不同时刻前沿界面的三维视图。

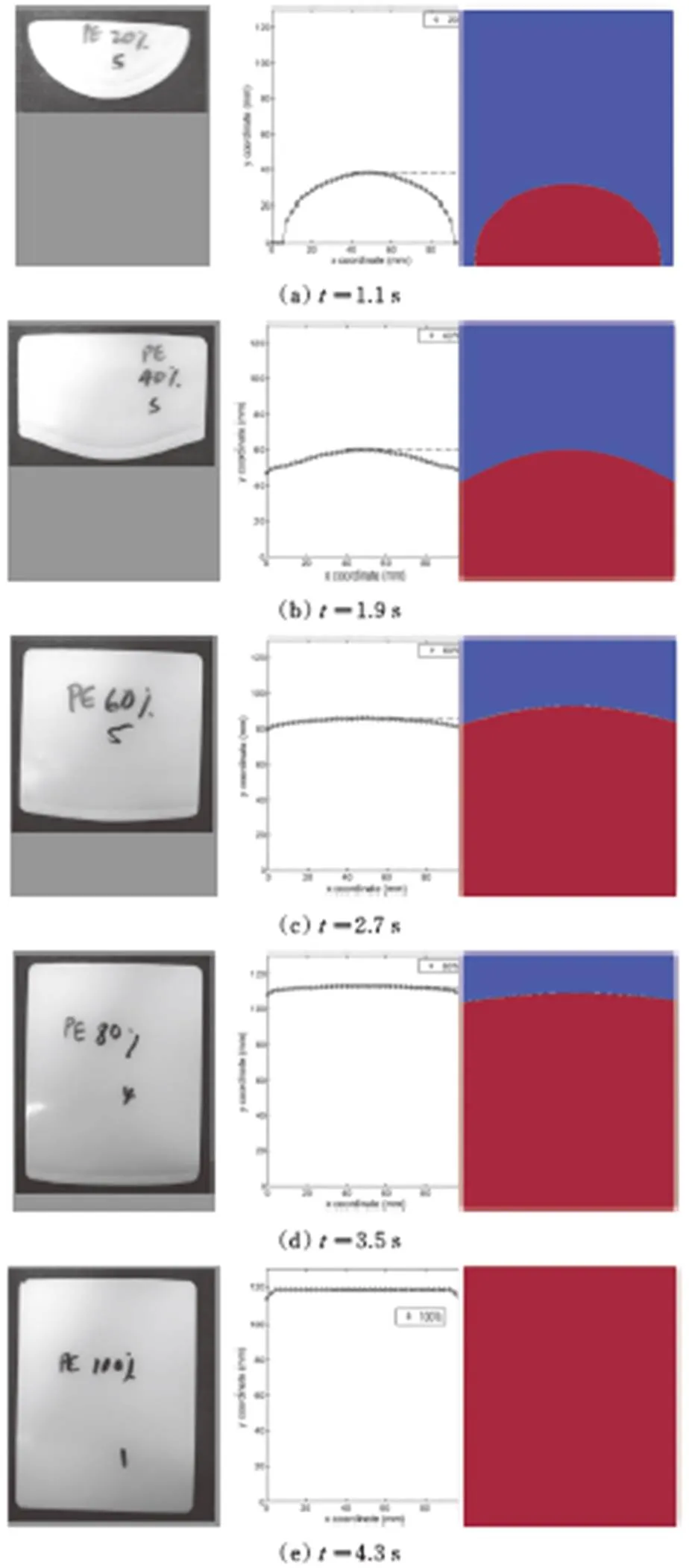
图9　不同时刻的实验结果（左）、文献［9］的数值结果（中）和本文的数值结果（右）

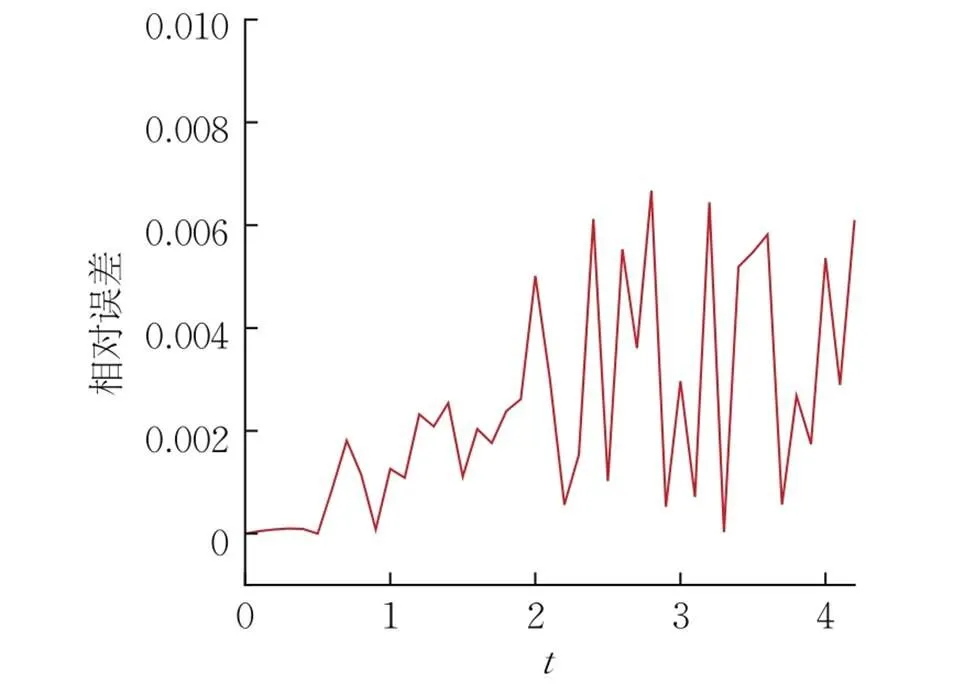
图10　网格3熔体质量相对误差随时间的变化

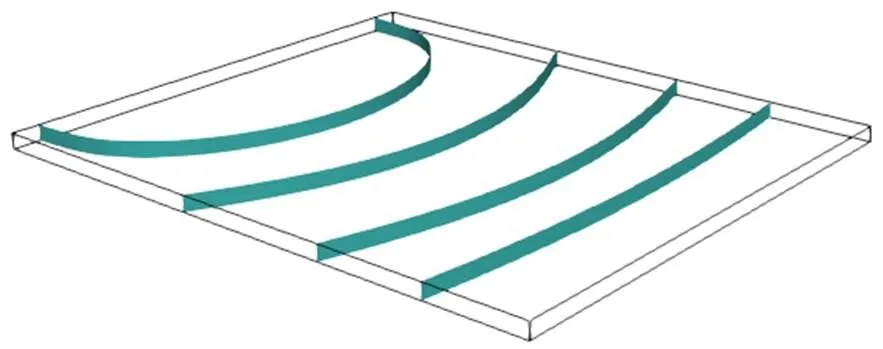
图11　不同时刻前沿界面的三维视图

4　结论

提出了三维情形下的有限元-间断有限元耦合算法，并基于非牛顿-牛顿两相流计算模型，数值模拟了三维非牛顿流体的充填过程。在三维圆球剪切流动的数值算例中，圆球形状演化趋势和文献［18-19］的描述一致，当自由界面发生最大变形时亦未出现任何不稳定现象，在充填过程中，网格3熔体质量最大相对误差为1.5%。在三维矩形型腔非牛顿流体的充填过程中，前沿界面非常稳定，在初始阶段，前沿界面呈圆弧状，随着时间的进展，逐渐变平缓，前沿界面的演化趋势与实验结果及文献［9］的结果相吻合，在充填过程中，网格3非牛顿流体质量的最大相对误差为0.67%。数值结果表明，本文的有限元-间断有限元耦合算法能稳定、有效、准确地模拟三维非牛顿流体的充填过程，并保证了流体具有较好的质量守恒性。

［1］ XU X Y， OUYANG J， YANG B X， et al. SPH simulations of three-dimensional non-Newtonian free surface flows［J］. Computer Methods in Applied Mechanics and Engineering， 2013， 256： 101-116. DOI：10.1016/j.cma.2012.12.017

［2］ FIGUEIREDO R A， OISHI C M， CUMINATO J A， et al. Three-dimensional transient complex free surface flows： Numerical simulation of XPP fluid［J］. Journal of Non-Newtonian Fluid Mechanics， 2013， 195： 88-98. DOI：10.1016/j.jnnfm.2013.01.004

［3］ ZHANG C H， CHEN S G， SUN Q C， et al. Free-surface simulations of Newtonian and non-Newtonian fluids with the lattice Boltzmann method［J］. Acta Geologica Sinica（English Edition）， 2016， 90（3）： 999-1010. DOI：10.1111/1755-6724.12740

［4］ 周文，欧阳洁，杨斌鑫，等. 三维非等温非牛顿流体充模过程的建模与模拟［J］. 化工学报， 2011， 62（3）： 618-627.

ZHOU W， OUYANG J， YANG B X， et al. Modeling and simulation of 3D mold filling process for non-isothermal non-Newtonian fluid［J］. CIESC Journal， 2011， 62（3）： 618-627.

［5］ BAUM M， ANDERS D. A numerical simulation study of mold filling in the injection molding process［J］. Computer Methods in Materials Science， 2021， 21（1）： 25-34. DOI：10.1002/fld.166

［6］ LI Q， QU F C. A level set based immersed boundary method for simulation of non-isothermal viscoelastic melt filling process［J］. Chinese Journal of Chemical Engineering， 2021， 32： 119-133. DOI：10.1016/j.cjche.2020.09.057

［7］ XU X Y， TIAN L Y， PENG S， et al. Development of SPH for simulation of non-isothermal viscoelastic free surface flows with application to injection molding［J］. Applied Mathematical Modelling， 2022， 104： 782-805. DOI：10.1016/j.apm.2021.12.015

［8］ TOMÉ M F， CASTELO A，NÓBREGA J M， et al. Numerical and experimental investigations of three-dimensional container filling with Newtonian viscous fluids［J］. Computers & Fluids， 2014， 90： 172-185. DOI：10.1016/j.compfluid.2013.11.015

［9］ MUKRAS S M S， AL-MUFADI F A. Simulation of HDPE mold filling in the injection molding process with comparison to experiments［J］. Arabian Journal for Science and Engineering， 2016， 41（5）： 1847-1856. DOI：10.1007/s13369-015-1970-9

［10］LIU Q S， OUYANG J， ZHOU W， et al. Numerical simulation of the sequential coinjection molding process based on level set method［J］. Polymer Engineering & Science， 2015， 55（8）： 1707-1719. DOI：10.1002/pen.24009

［11］LIU Q S， OUYANG J， LI W M， et al. Three-dimensional modelling and simulation of sequential co-injection moulding with application to a toothbrush handle［J］. The Canadian Journal of Chemical Engineering， 2016， 94（2）： 382-390. DOI：10.1002/cjce.22394

［12］ZHUANG X， OUYANG J， LI W M， et al. Three-dimensional simulations of non-isothermal transient flow and flow-induced stresses during the viscoelastic fluid filling process［J］. International Journal of Heat and Mass Transfer， 2017， 104： 374-391. DOI：10. 1016/j.ijheatmasstransfer.2016.08.064

［13］HE L P， LU G， CHEN D C， et al. Three-dimensional smoothed particle hydrodynamics simulation for injection molding flow of short fiber-reinforced polymer composites［J］. Modelling and Simulation in Materials Science and Engineering， 2017， 25（5）： 055007.

［14］BORZENKO E I， HEGAJ E I. Three-dimensional simulation of a tank filling with a viscous fluid using the VOF method［J］. Journal of Siberian Federal University （Mathematics & Physics）， 2020， 13（6）： 670-677. DOI：10.17516/1997-1397-2020-13-6-670-677

［15］GU Z H， WEN H L， YU C H， et al. Interface-preserving level set method for simulating dam-break flows［J］. Journal of Computational Physics， 2018， 374： 249-280. DOI：10.1016/j.jcp.2018.07.057

［16］AGUIRRE A， CASTILLO E， CRUCHAGA M， et al. Stationary and time-dependent numerical approximation of the lid-driven cavity problem for power-law fluid flows at high Reynolds numbers using a stabilized finite element formulation of the VMS type［J］. Journal of Non-Newtonian Fluid Mechanics， 2018， 257： 22-43. DOI：10.1016/j.jnnfm.2018.03.014

［17］GUERMOND J L， MINEV P， SHEN J. An overview of projection methods for incompressible flows［J］. Computer Methods in Applied Mechanics and Engineering， 2006， 195（44-47）： 6011-6045. DOI：10.1016/j.cma.2005.10.010

［18］GUERMOND J L， de LUNA M Q， THOMPSON T. An conservative anti-diffusion technique for the level set method［J］. Journal of Computational and Applied Mathematics， 2017， 321： 448-468. DOI：10.1016/j.cam.2017.02.016

［19］LUO K， SHAO C X， YANG Y， et al. A mass conserving level set method for detailed numerical simulation of liquid atomization［J］. Journal of Computational Physics， 2015， 298： 495-519. DOI：10.1016/j.jcp.2015.06.009

The numerical investigation of non-Newtonian fluid filling process via finite element and discontinuous Galerkin method

GAO Puyang

（，，710064，）

In this paper, we develop a coupled finite element and discontinuous Galerkin method in three dimension and study the non-Newtonian fluid filling process. To solve two phase Navier-Stokes equations, we employ the incremental pressure correction scheme to accomplish it in three steps. In order to guarantee the computational stability, we take the second order and first order interpolation polynomials for the velocity and pressure, respectively. In addition, the conservative Level Set method is employed to capture the moving interface. The discontinuous Galerkin method is used to solve the Level Set and its re-initialization equations. We take the three dimensional vortex shearing problem and the three dimensional non-Newtonian fluid filling process to verify the proposed approach, compare the result with the numerical results and existing experimental data to illustrate the stability, accuracy and the mass conservation property of the coupled scheme.

finite element; discontinuous Galerkin; level set; non-Newtonian filling process

O 242.1

A

1008⁃9497（2023）01⁃049⁃07

2021⁃12⁃13.

国家自然科学基金资助项目（11901051，11971075）；陕西省自然科学基础研究计划青年项目（2020JQ-338）；长安大学中央高校基本科研业务费项目（300102122107）；陕西省科学技术协会青年人才托举计划项目（20220504）.

高普阳（1991—），ORCID：https：//orcid.ord/0000-0001-8620-1783，男，博士，讲师，主要从事非牛顿流动问题的数值算法研究，E-mail： gaopuyang@chd.edu.cn.