混合偏导数相等的若干充分条件的注记

江樵芬， 阮颖彬， 徐 起

(1.福建师范大学 数学与统计学院，福州 350117； 2.厦门大学 数学科学学院，福建 厦门 361005)

1 引 言

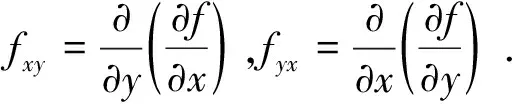
定理1(Clairaut定理、Schwarz定理)设fx,fy,fxy和fyx在点(x0,y0)的某邻域内存在，fxy和fyx在点(x0,y0)连续，则fxy(x0,y0)=fyx(x0,y0).

定理2(Peano的结果)设fx,fy和fyx在点(x0,y0)的某邻域内存在，fyx在点(x0,y0)连续，则fxy(x0,y0)也存在，且fxy(x0,y0)=fyx(x0,y0).

定理3(Young的结果)设fx,fy在点(x0,y0)的某个邻域内存在且在点(x0,y0)可微，则有fxy(x0,y0)=fyx(x0,y0).

文献[1-4]尝试减弱以上定理的条件，以期给出适用范围更广的混合偏导数相等的充分条件.本文对文献[1-4]给出的若干充分条件及其证明的正确性提出质疑，深入分析其证明的错误之处，并给出反例说明有些充分条件不成立.

本文将从分析Clairaut定理、Peano的结果、Young的结果的证明思路出发，深入思考文献[1-5]中一些证明的错误原因，尝试去理清其证明的逻辑，发现问题所在，并给出教学上的建议.

2 二阶混合偏导数相等的本质及证明思路分析

注意到

若记

F(Δx,Δy)=f(x0+Δx,y0+Δy)-f(x0,y0+Δy)-f(x0+Δx,y0)+f(x0,y0)，

在证明中一般对函数F(Δx,Δy)作如下处理.

若fxy在(x0,y0)的某邻域内存在，令φ(x)=f(x,y0+Δy)-f(x,y0)，则

F(Δx,Δy)=φ(x0+Δx)-φ(x0)=φ′(x0+θ1Δx)Δx

=(fx(x0+θ1Δx,y0+Δy)-fx(x0+θ1Δx,y0))Δx

=fxy(x0+θ1Δx,y0+θ2Δy)ΔxΔy(0<θ1,θ2<1).

若fyx在(x0,y0)的某邻域内存在，令ψ(x)=f(x0+Δx,y)-f(x0,y)，则

F(Δx,Δy)=ψ(y0+Δy)-ψ(y0)=ψ′(y0+θ3Δy)Δy

=(fy(x0+Δx,y0+θ3Δy)-fy(x0,y0+θ3Δy))Δy

=fyx(x0+θ4Δx,y0+θ3Δy)ΔxΔy， (0<θ3,θ4<1).

则

由此，若fxy，fyx在(x0,y0)连续，容易知fxy(x0,y0)=fyx(x0,y0).这就证明了Clairaut定理.

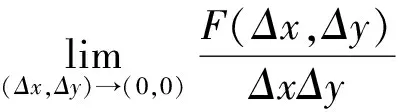
Young的结果的证明与上述两个充分条件的证明略有不同.它是这样处理的.

若fx在(x0,y0)可微，则对充分小的Δx，Δy

从而

当Δx=Δy=h>0时，有

以上三个充分条件的证明容易在多本流行的教科书或习题集中查到，故没有给出出处.详细分析其证明思路是为了下文与错误证明做比较.

3 对一些充分条件及其证明的质疑

在上述证明思路的分析中，可以看到在处理F(Δx,Δy)时都固定了某个分量，对另一分量应用拉格朗日中值定理.应该注意到拉格朗日中值定理中存在的中值点既依赖于所讨论的函数，也依赖于所讨论的区间.忽略中值点对函数与区间的依赖性将导致错误,一元情况下与此类中值点有关的隐蔽性错误的讨论可以见文献[6].而在二元情况下，固定二元函数的某个分量得到的一元函数，一般与所固定的那个分量的值有关，所固定分量的不同取值对应不同的一元函数，由此得到的中值点一般与被固定的分量相关.如在得到

F(Δx,Δy)=fxy(x0+θ1Δx,y0+θ2Δy)ΔxΔy

的过程中，不同的Δy确定了不同的函数φ(x)，不同的φ(x)存在的θ1一般不同，因此θ1一般与Δy有关，同理θ2与Δx有关.这种依赖性比一元的情况更隐蔽，更容易被忽略，因此也更容易导致错误.以下关于混合偏导数相等的错误证明，其错误原因莫不如是(除了例5)，并且这些错误几乎没有被意识到(至少就笔者检索到的文献而言).下面笔者逐一分析其错误原因，并对错误结论给出反例加以说明.

例1[5](Peano的结果的错误证明) 设fx,fy在点(x0,y0)的某邻域内存在，fxy在点(x0,y0)连续，则fyx(x0,y0)也存在，且fyx(x0,y0)=fxy(x0,y0).

错误证明如前所述，由于fxy在(x0,y0)的邻域内存在，则

F(Δx,Δy)=fxy(x0+θ1Δx,y0+θ2Δy)ΔxΔy(0<θ1,θ2<1).

上式两边同除以Δy，并令Δy→0，由偏导数的定义及fxy在(x0,y0)连续就得到

fy(x0+Δx,y0)-fy(x0,y0)=fxy(x0+θ1Δx,y0)Δx.

再在上式两边同除以Δx，并令Δx→0，由fxy在(x0,y0)的连续性得到fyx(x0,y0)=fxy(x0,y0).

错因分析这个证明不是利用二重极限与累次极限的关系，而是先对Δy取极限得到

fy(x0+Δx,y0)-fy(x0,y0)=fxy(x0+θ1Δx,y0)Δx

再对Δx取极限得fyx(x0,y0)=fxy(x0,y0).厦门大学的刘轼波教授曾在福建省“数学分析”与“高等数学”第七次课程建设研讨会上指出这里存在的一个错误：它是利用fxy在(x0+θ1Δx,y0)的连续性得到

而不是利用fxy在(x0,y0)的连续性.这引起了笔者的注意.受其启发，在细读该证明之后,发现这里还有一个隐蔽的错误：θ1可能是与Δy有关的, 对Δy取完极限的式子中不应该还有Δy.因此

并不一定成立.证明走不下去.

如果忽略了θ1对Δy的依赖性，这种错误的证法会引发人们去思考更弱一些的条件，利用这种错误的证法得到一些看起来更好的结论(但实际上却是错误的).

例2[1](Peano的结果的错误推广) 若f(x,y)在点(x0,y0)的邻域U(x0,y0)有定义，满足

(i)fx(x,y),fy(x,y)在U(x0,y0)存在；

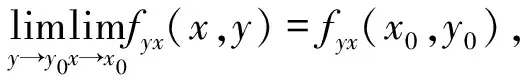
则fxy(x0,y0)存在，并有fxy(x0,y0)=fyx(x0,y0).

错误证明如前所处理一般有

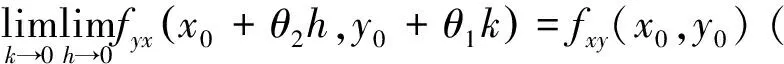
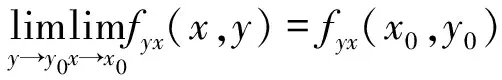
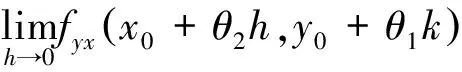
进而得不到fyx(x0,y0)=fxy(x0,y0).

笔者将在例4后面给出反例说明这个充分条件是错误的.

文献[2]给出了Clairaut定理的一种推广，但它的证明存在错误.

例3[2](Clairaut定理的存疑推广) 设二元函数f的混合偏导数fxy和fyx在点(x0,y0)的某邻域内存在，fxy在点(x0,y0)关于x连续，fyx在点(x0,y0)关于y连续，则有

fxy(x0,y0)=fyx(x0,y0).

错误证明若fxy在(x0,y0)的某邻域内存在，如前所述有

F(Δx,Δy)=(fx(x0+θ1Δx,y+Δy)-fx(x0+θ1Δx,y0))Δx

=(fxy(x0+θ1Δx,y0)Δy+o(Δy))Δx.

则

若fyx在(x0,y0)的某邻域内存在，同理也有

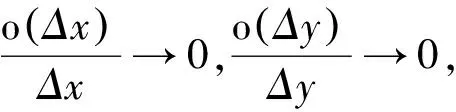
错因分析首先θ1可能与Δy有关，则

未必成立.从而

fx(x0+θ1Δx,y0+Δy)-fx(x0+θ1Δx,y0)=fxy(x0+θ1Δx,y0)Δy+o(Δy)

也未必成立.证明到此进行不下去.

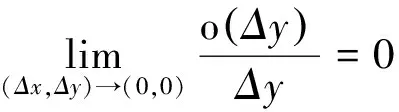
例4[3](Peano的结果的错误推广) 若二元函数f的偏导数fx,fy及fyx在点(x0,y0)的某个邻域内存在，且fyx在点(x0,y0)关于y连续，则fxy在点(x0,y0)存在，且fxy(x0,y0)=fyx(x0,y0).

但事实上可以找到反例说明例4所给的充分条件是错误的.这也从另一个侧面说明例3的证明是错误的.

反例令

计算可得

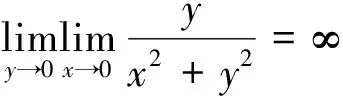
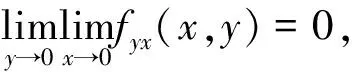
文献[4]中给出了Young的结果的推广,它把条件 “fx,fy在点(x0,y0)可微”减弱为“fy或fx在(x0,y0)可微”，但它的证明同样存在问题.

例5[4](Young的结果的存疑推广) 设fx,fy在(x0,y0)的某邻域内存在，fy(或fx)在(x0,y0)可微，则fxy(x0,y0)(或fyx(x0,y0))也存在且fxy(x0,y0)=fyx(x0,y0).

错误证明若fy在(x0,y0)可微，则对充分小的Δx,Δy，

F(Δx,Δy)=(fy(x0+Δx,y0+θ1Δy)-fy(x0,y0+θ1Δy))Δy

=fyx(x0,y0)ΔxΔy+α(Δx,Δy)ΔxΔy+(β1(Δx,Δy)-β2(Δx,Δy))θ1(Δy)2，

其中

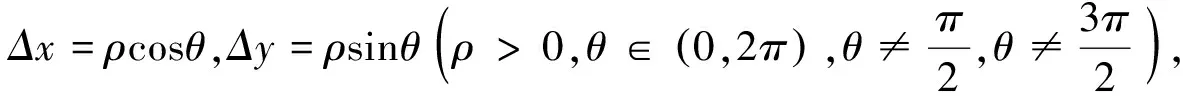
从而

再由二重极限与二次极限的关系可知fxy(x0,y0)=fyx(x0,y0).

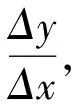
4 结 论

本文质疑了Clairaut定理的一个推广、Peano的结果的一种证明及两个推广、Young的结果的一个推广，同时给出反例说明Peano的结果的两个推广是错误的.这些证明错误的原因(除了例5)都是类似的：固定二元函数的某个分量，把它视为另一分量的一元函数，对它使用拉格朗日中值定理时忽略了中值点对另一分量的依赖.对于此类错误，建议在教学中将二元函数看作一元函数时，应强调此一元函数对所固定分量的依赖.在对这类一元函数运用微分中值定理时所存在的中值点不妨记为θΔx或θΔy，用其中的下标来体现依赖性.

遗憾的是对于Clairaut定理的推广及Young的结果的推广，笔者既给不出正面的证明，也无法给出反例说明其是错误的，这需要进一步的思考.

致谢感谢审稿专家对本文的有益建议以及相关参考文献对本文的启发.