与广义Witt代数有关的非有限分次李代数的极大子代数及其性质
2023-01-14徐润果
徐润果, 许 莹
(合肥工业大学 数学学院,合肥 230601)
1 引 言
Witt代数是经典微分和积分学中的一个重要例子,它与拓扑学和几何学有着密切联系,同时也具有很多特殊的代数性质.Witt代数具体定义为Laurent多项式代数[t,t-1]上的单变量的复导子李代数,即[t,t-1]上线性算子D的李代数,并且该算子满足莱布尼茨公式D(ab)=D(a)b+aD(b).许多专家学者对Witt代数展开了研究,例如文献[1]和[2]等采取多种方式,对Witt代数进行新的构造与变形,丰富了李理论.文献[3]由带单位元的交换结合代数和阿贝尔导子代数对构造出Witt型李代数,与文献[4]以及文献[5]定义的李代数相比,该代数更为一般.文献[6]建立了Passman构造的Witt型单李代数的同构类,并给出了广义Witt代数W(l1,l2,l3;Γ)的定义,而本文将要讨论的非有限分次李代数W正是该代数的一种特殊情况W(1,0,1;),具体定义详见定义1和定义2.除此之外,Schrödinger-Virasoro代数也是-分次李代数, 文献[7]生动刻画了其扭代数的泊松结构,而文献[8]确定并分类了与该李代数相关的秩为3的李共形代数的结构.
2000年后,广义Witt代数的2-上同调群[9]和李双代数结构[10]也得到了充分的考察与构建.文献[11]对Witt和Virasoro代数进行了推广,文献[12]量子化了特征为0的广义Witt代数的李双代数结构.文献[13]证明了任何单变量的广义Witt代数都是半单的、不可分解的李代数,它不包含任何维数大于1的阿贝尔李子代数.从那时起,广义Witt型代数得到了广泛的研究.另外,在广义Witt型代数[14]的基础上,从结合代数的角度出发构造出了广义Weyl型代数[15],进而得出了其2-上同调群[16]等一系列的成果.
代数的极大子代数可以深刻的反映代数的内部特征,然而目前对Witt代数的极大子代数研究工作较少.显然,非有限分次李代数W有很多子代数,例如上文提到的经典Witt代数和Heisenberg-Virasoro代数[17].此外,文献[18]研究了素特征域上Witt代数的极大子代数的2-局部导子,文献[19]对一类广义Witt的子代数做出研究并构造出所有的自同构类.广义Witt代数作为较复杂的李代数,研究其极大子代数的工作显得尤为重要.本文提出了非有限分次李代数W的3个极大子代数W1,W2,W3,利用李代数的特性研究了相关性质.并且证明了前两个子代数是同构的,进一步丰富了广义Witt代数的研究理论.
2 广义Witt代数及非有限分次代数
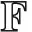

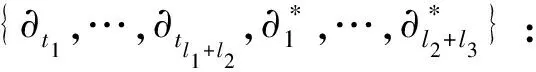
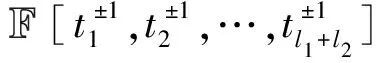
对于任意的1≤i≤l1,1≤j≤l2,1≤k≤l3.

[u∂i,v∂j]=u∂i(v)∂j-v∂j(u)∂i,
对于∀u,v∈A(l1,l2,l3;Γ),1≤i,j≤l1+l2+l3.
由此,就得到了广义Witt李代数W(l1,l2,l3;Γ).现在令l1=1,l2=0,l3=1,Γ=,可以得到本文研究的非有限分次李代数W.确切地说,A(1,0,1;)是自由的[t±1]-模,α∈从高维向量变成了一个数.对于任意的α,i∈,令Iα,i=xαti∂1,Lα,i=xαti∂2, 其中∂1(xαti)=ixαti-1,∂2(xαti)=αxαti.W的详细定义如下:
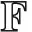
[Lα,i,Lβ,j]=(β-α)Lα+β,i+j, [Lα,i,Iβ,j]=βIα+β,i+j-iLα+β,i+j-1, [Iα,i,Iβ,j]=(j-i)Iα+β,i+j-1,
对于任意的α,β,i,j∈.
下面阐述一些李理论的基础定义.
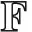
定义4设g是李代数,N是g的子空间.如果[g,N]⊆N,则N称为g的理想.
特别地,[g,g]也是g的理想,且称[g,g]为g的导出代数或导代数.据此,可以做出g的一个理想序列:
g(0)=g,g(1)=[g,g],g(2)=[g(1),g(1)],…
显然有
g=g(0)⊇g(1)⊇…⊇g(i)⊇g(i+1)⊇…,
称上述理想列为g的导代数序列或导出列.
定义5李代数g称为可解李代数,如果存在正整数n使得g(n)=0.
定义6若李代数g不含任何非零的可解理想, 则g称为半单李代数.
3 非有限分次李代数W及其极大子代数
在本章节, 将分析非有限分次李代数W的性质,并且给出其两个极大子代数,且对其性质分别做出阐述.
3.1 非有限分次李代数W
前文已经得到了非有限分次李代数W,进一步地,注意到该代数的性质,这导致了W与其他代数的不同之处.
引理1W是单李代数[6].
根据上述引理,可以推断出W的中心Z(W)={0}.事实上,这个结论也可以由W本身的构造得到,证明如下.
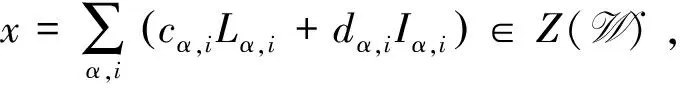
比较各项系数可得:cα,i(β-α)=0,dα,iα=0.又由于β的任意性,故有
cα,i=0, ∀α,i∈,dα,i=0, ∀α≠0,i∈,
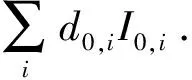
根据任意选取的j可知d0,i=0,所以x=0,即Z(W)={0}.
3.2 极大子代数W1及其性质
定理1W1=span{Lα,i,I0,j|∀α,i,j∈} 是W的极大子代数.
证(i)对于任意的α,β,i,j∈,有
[Lα,i,Lβ,j]=(β-α)Lα+β,i+j, [Lα,i,I0,j]=-iLα,i+j-1, [I0,i,I0,j]=(j-i)I0,i+j-1,
则W1对于李括号的运算是封闭的,再由Lα,i,I0,j的线性结构知:W1是W的子代数.

其中q是最小非零系数指标,p是最大非零系数指标.将I0,q从左端作用于y,
类似地,反复用适当的I0,k作用,最终得到下式
其中-γ是最小非零系数指标,μ是最大非零系数指标.
下面分析-γ<0<μ的情形:
将L1,0作用于z,即得
[L1,0,z]=-γc-γ,mI1-γ,m+…+c1,mI2,m+…+μcμ,mI1+μ,m;
令L1,0反复作用γ次于上式,即得
(γ+1)!c1,mIγ+2,m+…+μ…(μ+γ)cμ,mIγ+μ+1,m,
此时消去了前γ+1项;同理,反复用适当的Lη,0作用,最终将只剩下一非零项Iη,m∈N(总可以进行适当的施用,使得η≠0,否则没有意义).
对于任意的m∈,I0,1-m∈W1,[I0,1-m,Iη,m]=(2m-1)Iη,0,[Iη,0,I0,j+1]=(j+1)Iη,j, 故当j≠-1时,Iη,j∈N;[Iη,1,I0,-1]=-2Iη,-1, 故Iη,-1∈N.即∀j∈,Iη,j∈N.又[Lθ-η,0,Iη,j]=ηIθ,j∈N,而η≠0,Iθ,j∈N,∀θ,j∈.
γ,μ取值的其他情况同理可得.
又因W1⊆N,则Lθ,j∈N,对于任意的θ,j∈.综上,N=W,即W1=span{Lα,i,I0,j|∀α,i,j∈} 是W的极大子代数.
性质1W′1=span{Lα,i|∀α,i∈}是W1的理想:
(i)W′1是W1唯一的非平凡理想;
(ii)[W′1,W′1]=W′1.
证W′1是W1的理想这一结论可以从W1的封闭性验证中直接得出.下证(i)和(ii):

(a)将L0,0作用于x,
其中β是最小非零系数指标,γ是最大非零系数指标.
用Lβ,0作用于y,可得
同理,反复用适当的Lη,0作用,最终将得到下式
其中-q是最小非零系数指标,p是最大非零系数指标.下面我们分析-q<0 使I0,0作用一次于z,可得 [I0,0,z]=-qcλ,-qLλ,-q-1+…+(-cλ,-1)Lλ,-2+…+pcλ,pLλ,p-1; 用I0,0作用p+1次后,即得 (-q)…(-q-p)cλ,-qLλ,-q-p-1+…+(-1)…(-p-1)cλ,-1Lλ,-p-2, 即可消去若干项.同理,反复用适当的I0,k作用,最终将只剩下一非零项Lλ,h∈W′.∀ζ,m∈,Lζ-λ,m-h∈W1,[Lλ,h,Lζ-λ,m-h]=(ζ-2λ)Lζ,m, 故当ζ≠2λ时,Lζ,m∈W′;[L-1,0,L2λ+1,m]=(2λ+2)L2λ,m,故当λ≠-1时,L2λ,m∈W′.[L-3,0,L1,m]=4L-2,m∈W′,即对于任意的ζ,m∈,Lζ,m∈W′. q与p取值的其他情况同理可得. 其中u是最小非零系数指标,v是最大非零系数指标. 把I0,u作用于r, 可得[I0,u,r]=bu+1I0,2u+…+(v-u)bvI0,v+u-1;同理,反复用适当的I0,t作用,最终将只剩下一个非零项I0,l∈W′.对于任意的k∈,I0,k-l+1∈W′1,[I0,l,I0,k-l+1]=(k-2l+1)I0,k,故当k≠2l-1时,I0,k∈W′;[I0,0,I0,2l]=2lI0,2l-1,故当k≠0时,I0,2k-1∈W′;[I0,-2,I0,2]=4I0,-1, 故当k≠0时,I0,-1∈W′. 综上所述,对于任意的k∈,I0,k∈W′.即证W′=W1,故W1除W′1外无非平凡理想. (ii)由理想的定义,可自然发现[W′1,W′1]⊆W′1,下证反方向的包含关系: 对于任意的α,i∈,Lα,i都可以由 得到,其中 即Lα,i∈[W′1,W′1],故[W′1,W′1]⊇W′1,即证[W′1,W′1]=W′1. 据此性质,利用定义5和定义6不难验证以下两个推论: 推论1W′1不是可解李代数. 推论2W1是半单李代数. 定理2W2=span{Lα,0,Iβ,j|∀α,β,j∈} 是W的极大子代数. 证(i)对于任意的α,β,i,j∈, 有 [Lα,0,Lβ,0]=(β-α)Lα+β,0, [Lα,0,Iβ,j]=βIα+β,j, [Iα,i,Iβ,j]=(j-i)Iα+β,i+j-1, 则W2对于李括号的运算是封闭的,再由Lα,0,Iβ,j的线性结构知:W2是W的子代数. 其中-β是最小非零系数指标,γ是最大非零系数指标. 类似于性质1中(a)的证明,选取合理的Lη,0,I0,k多次作用于y,可得对于任意的ζ,m∈,Lζ,m∈N.又由于W2N,则对于任意的ζ,m∈,Iζ,m∈N.也就是说,N=W,即W2=span{Lα,0,Iβ,j|∀α,β,j∈} 是W的极大子代数. 发现W1与W2满足如下关系: 引理2W1≅W2. 证对于任意的α,i∈,定义Φ:W1→W2,Lα,iIi,α+1,I0,iLi-1,0.显然这是一个线性映射,且是双射.下证它是同态映射: 对于任意的α,β,i,j∈, Φ([Lα,i,Lβ,j])=Φ((β-α)Lα+β,i+j)=(β-α)Ii+j,α+β+1, Φ([Lα,i,I0,j])=Φ(-iLα,i+j-1)=-iIi+j-1,α+1, Φ([I0,i,I0,j])=Φ((j-i)I0,i+j-1)=(j-i)Li+j-2,0. 另一方面 [Φ(Lα,i),Φ(Lβ,j)]=[Ii,α+1,Ij,β+1]=(β-α)Ii+j,α+β+1, [Φ(Lα,i),Φ(I0,j)]=[Ii,α+1,Lj-1,0]=-iIi+j-1,α+1, [Φ(I0,i),Φ(I0,j)]=[Li-1,0,Lj-1,0]=(j-i)Li+j-2,0. 从而任意的x,y∈W1,Φ([x,y])=[Φ(x),Φ(y)];易见,变换Φ也满足这样的线性关系式 Φ(kx+by)=kΦ(x)+bΦ(y), ∀k,b∈,x,y∈W1. 综合以上分析,Φ是W1→W2的同构映射,即证本引理. 由于W1与W2同构,类似于W1的性质,自然地,W2也有如下性质和推论: 性质2W′2=span{Iα,i|∀α,i∈}是W1的理想: (i)W′2是W2唯一的非平凡理想; (ii)[W′2,W′2]=W′2. 推论3W′2不是可解李代数. 推论4W2是半单李代数. 根据前文集中讨论,两个W的极大子代数W1,W2已经被清晰的表示出来.下面考虑W的另一极大子代数W3,该代数的结构与前两个代数稍有不同. 定理3W3=span{βIβ,j-jLβ,j-1|∀β,j∈} 是W的极大子代数. 证(i)∀α,β,i,j∈, 总有 [αIα,j-jLα,j-1,βIβ,i-iLβ,i-1]=(αi-βj)((α+β)Iα+β,i+j-1-(i+j-1)Lα+β,i+j-2), 则W3对于李括号的运算是封闭的.根据元素βIβ,j-jLβ,j-1的线性得:W3是W的子代数. 显而易见,W3包含这样的元素{L0,i,Iα,0|∀α,i∈}. (ii)由前面已知,W3⊆W.由于该子代数的特殊构造,下证W3≠W,即存在 比较各项系数后,可得以下结论: 观察上式两端所有的I1,i系数,有c1,1=-1;c1,i=0,若i≠1.据此分析有L1,0=-I1,1+L1,0,这显然是矛盾的.因此,L1,0∉W3,即有W3≠W. (iii)设N也是W的子代数且有W3N⊆W. 其中x*∈W3,dγ,m∶fγ,m≠γ∶m,这可以由W中元素的线性性质推导出.事实上,对于任意的γ,m∈, Iγ,m∈W,Iγ,m=(γIγ,m-mLγ,m-1)-((γ-1)Iγ,m-mLγ,m-1); Lγ,m∈W,Lγ,m=(γIγ,m+1-(m+1)Lγ,m)+(-γIγ,m+1+(m+2)Lγ,m). 令y=x-x*,特别注意的一点是,y的求和项不包含这样的项L0,i,Iα,0,则γ,m≠0. (b)用L0,1作用于y, 上式加上一些W3中的项 同样,该式不包含这样的项L0,i. (c)若上述求和项只包含一项,则直接进入下一步;否则使用数学归纳法:项数为1时,显然成立;假定项数≤n时,通过适当的李括号消项可获得一项,下证项数为n+1 时可获得一项.对于项数为n+1的和式 此排序是先后按第一、二指标的从小到大排列.把L0,-q,I0,0先后作用于上式左端 [I0,0,[L0,-q,gλ,qLλ,q+…+gλ,pLλ,p+…+gη,uLη,u+…+gη,vLη,v]] =[I0,0,gλ,qλLλ,0+gλ,q+1λLλ,1+…+gλ,pλLλ,p-q+…+gη,uηLη,u-q+…+gη,vηLη,v-q] =gλ,q+1λLλ,0+…+gλ,pλ(p-q)Lλ,p-q-1+…+gη,uη(u-q)Lη,u-q-1+…+gη,vη(v-q)Lη,v-q-1. (d)对于x1:对于任意的β,j∈, [x1,L0,j-i]=[Lα,i,L0,j-i]=-αLα,j, [Lα,j,Iβ-α,0]=(β-α)Iβ,j-jLβ,j-1, (βIβ,j-jLβ,j-1)-((β-α)Iβ,j-jLβ,j-1)=αIβ,j, 由于α≠0及以上分析易知Iβ,j∈W3+{x1}; βIβ,j+1-(βIβ,j+1-(j+1)Lβ,j)=(j+1)Lβ,j, 说明当j≠-1时,Lβ,j∈W3+{x1};[Lβ,0,L0,-1]=-βLβ,-1,由此说明当β≠0时,Lβ,-1∈W3+{x1},又L0,-1∈W3. 综上所述,对于任意的β,j∈,Lβ,j,Iβ,j∈W3+{x1}⊂N.这也验证了N=W,即有子代数W3=span{βIβ,j-jLβ,j-1|∀β,j∈} 的极大性. 非有限分次李代数W结构稍显复杂,为了方便研究其结构和表示理论,本文通过李括号运算的方法构造出3个极大子代数(见定理1、定理2、定理3).在李理论的支持下,得出了极大子代数的生成元及相关性质,且有W1≅W2(见引理2).值得一提的是,本文讨论的课题是广义Witt代数中重要的一部分,本论文中给出的方法具有普遍的适用性,可以解决广义Witt代数的子代数的相关研究问题.除此之外,非有限分次李代数W还有很多有趣的研究课题[20-21],希望本文中提出的方法和结论能对该代数的结构和表示理论等方面的探索有积极作用. 致谢作者非常感谢相关文献的启发以及相关审稿专家对本文提出的指导意见.3.3 极大子代数 W2及其性质

4 W的另一极大子代数

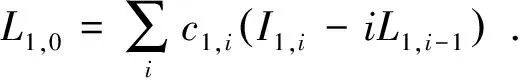


5 结 论
