季节性时间序列建模的“教”与“思”

韩 苗， 周圣武， 金子龙

(中国矿业大学 数学学院，江苏 徐州 221116)

1 引 言

季节变动，是指社会经济现象随着季节的变化而呈现的周期性变动.不分析研究、认识掌握现象的季节变化规律，常常会使模型的预测作用减弱甚至丧失.针对季节性时间序列，一般在统计预测课程教学中，可供选择的方法较多，如温特线性和季节性指数平滑模型、季节性交乘趋向模型、含虚拟变量回归模型、ARMA模型等方法[1-2].不同预测模型各具特点，在教学中为了综合比较这几种模型，本文从实际问题出发，探讨模型的应用实践.

国内生产总值GDP是衡量经济发展水平的重要指标之一，研究GDP的预测分析问题具有重要的实际意义.很多学者针对不同类型的数据，如季度GDP[3-5]、年度GDP[6]及地区GDP[7-9]等进行分析，追求预测精度更高的模型及算法.由于本文考察的是季节性时间序列建模方法，因此选取我国国内生产总值当季值(亿元)进行研究，基于四种传统的季节性时间序列预测方法进行统计建模，模型易于理解而且预测效果较优，为我国国内生产总值预测分析提供参考.在综合建模分析的基础上，强化应用实践，培养学生解决复杂问题的综合能力和高阶思维.

2 预测模型的构建

2.1 温特线性和季节性指数平滑模型

温特线性和季节性指数平滑模型是描述既有线性趋势又有季节变化序列的模型，一般有两种形式，一种是线性趋势与季节相乘形式；另一种是线性趋势与季节相加形式.这里考虑相乘形式，即Holter-Winter 季节乘积模型，预测模型为

Ft+m=(St+btm)It-L+m，

(1)

式(1)中，m为预测的超前期数，且包含时序的三种成分：平稳性(St)、趋势性(bt)、季节性(It).它们都是建立在三个平滑值基础上的，分别为

(2)

bt=β(St-St-1)+(1-β)bt-1， 0<β<1，

(3)

(4)

式中，L为季节周期长度.I为季节调整因子，α，β，γ为三个平滑参数.

2.2 季节性交乘趋向模型

季节性交乘趋向模型如下：

(5)

式中，Vt是时间序列的趋势项；fi是时间序列各季的季节指数，且

式中，Fi是各期实际的季节指数，由当期实际值除以趋势值得到，T是季节周期的长度，m是季节周期的个数.

2.3 含虚拟变量回归模型

在回归模型中，一般解释变量即自变量都是连续取值的，但实际问题中，影响被解释变量变化的可能还有一些属性变量.如学历、性别、职业对收入的影响；一些月度或季度数据可能会受季节的影响.为了量化这些因素，通常会根据因素的属性类别，构造只取“0”或“1”的虚拟变量.虚拟变量的引入通常有三种形式：加法形式、乘法形式、加乘同时引入形式.

对于一般的一元线性回归模型

yt=β0+β1xt+εt，

(6)

εt满足回归模型基本假设.加法形式是将虚拟变量直接加到上面模型中，即

yt=β0+β1xt+αDt+εt，

(7)

式中Dt是虚拟变量，只取“0”或“1”.乘法形式是将虚拟变量与解释变量相乘后引入模型，即

yt=β0+β1xt+γDtxt+εt.

(8)

加法与乘法同时引入的形式(加乘形式)是将虚拟变量直接加到模型中，同时又将虚拟变量与解释变量相乘后引入模型，即

yt=β0+β1xt+αDt+γDtxt+εt.

(9)

2.4 自回归移动平均(ARMA)模型

自回归移动平均(ARMA)模型是经典的时间序列分析方法，广泛应用于各个领域.该模型建模步骤主要包括平稳性检验、模型识别、模型建立与选择和预测.如果时间序列包含季节性和趋势性特征，可以通过d阶逐期差分和D阶季节差分使其平稳化，再建立ARMA模型.通常将模型记为ARIMA(p,d,q)(P,D,Q)s，具体形式如下：

φp(B)ΦP(Bs)(1-B)d(1-Bs)Dyt=θq(B)ΘQ(Bs)εt，

(10)

式中，p是自回归阶数；q是移动平均阶数；P是季节性自回归阶数；Q是季节性移动平均阶数.其中

φp(B)=1-φ1B-φ2B2-…-φpBp

是p阶自回归算子；

θq(B)=1-θ1B-θ2B2-…-θqBq

是q阶移动平均算子；

ΦP(Bs)=1-Φ1Bs-Φ2B2s-…-ΦPBPs

是季节性P阶自回归算子；

ΘQ(Bs)=1-Θ1Bs-Θ2B2s-…-ΘQBQs

是季节性Q阶移动平均算子.

3 中国国内生产总值预测分析

本文采用的数据为2000年第1季度至2020年第4季度中国国内生产总值当季值(亿元)季度数据，数据来源国家统计局，数据序列如图1所示.从长期来看，季度GDP序列总体呈现上升的趋势，并且具有明显的季节性特征.

图1 中国国内生产总值时序图

下面采用前面介绍的四种常用的季节性时间序列建模方法对我国国内生产总值进行预测分析.这里将2000年第1季度至2018年第4季度数据作为训练样本，用于建立模型，选取2019年第1季度至2020年第4季度数据作为测试样本以检验模型的预测效果，最终预测2021年的季度GDP数据.

3.1 温特线性和季节性指数平滑模型预测结果

建立温特线性季节性指数平滑模型，首先要给定初值，分别选取初值

初始季节指数可以通过下面公式计算

其中

其次，要选取平滑参数，这里通过反复试验，综合比较最终选取平滑参数分别为α=0.5，β=0.5，γ=0.6，利用式(1)—(4)计算可得各期预测值.

最终得到预测结果2001年第2季度至2018年第4季度预测期内的均方根误差RMSE=1759.115404，平均绝对百分误差MAPE=1.521%；2019年第1季度至2020年第4季度样本期外的均方根误差RMSE=13639.86425，平均绝对百分误差MAPE=4.166%.

3.2 季节性交乘趋向模型预测结果

根据季度GDP时间序列的非线性变化特征，建立如下季节性交乘趋向模型：

式中，β0+β1t+β2t2是GDP时间序列非线性趋势部分.

设国内生产总值当季值序列的趋势方程为

Vt=β0+β1t+β2t2，

采用最小二乘法，得到趋势的估计方程(括号中的数据为对应t检验统计量的值)：

且可以得到R2=0.981975，接近1，拟合程度高.F检验值为1988.43，显然F检验通过.D.W=2.098135，表明随机误差项不存在序列相关，趋势方程整体拟合效果较好.

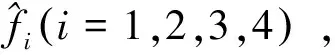
表1 季节指数与修正的季节指数

由上面结果可得

通过计算可得2000年第1季度至2018年第4季度预测期内的均方根误差RMSE=3697.749096，平均绝对百分误差MAPE=4.276%；2019年第1季度至2020年第4季度样本期外的均方根误差RMSE=14767.88079，平均绝对百分误差MAPE=4.716%.

3.3 含虚拟变量回归模型预测结果

这里通过引入虚拟变量来刻画季节性特征，同时因为时间序列具有递增的非线性趋势特征，在二次多项式函数趋势基础上，引入表示季节因素的虚拟变量，分别记作

由于引入虚拟变量，区分了不同季度的影响，更好的揭示了变量之间的关系，因此会提高预测精度.对于虚拟变量的引入，本文分别采用加法形式，乘法形式以及加乘同时引入形式模型.通过数值结果分析，模型优化，最终采用乘法形式的虚拟变量回归模型.具体模型如下：

yt=β0+β1t+β2t2+β3D1t×t+β4D2t×t+β5D3t×t+εt，

采用最小二乘法进行参数估计，估计结果见下表.

表2 含虚拟变量回归模型参数估计

模型整体拟合效果较好，通过预测分析，可得2000年第1季度至2018年第4季度样本期内的均方根误差RMSE=3714.049862，平均绝对百分误差MAPE=4.441%；2019年第1季度至2020年第4季度样本期外的RMSE=14027.03523，MAPE=3.921%.

3.4 ARMA模型预测结果

3.4.1 时间序列特征分析

首先对GDP当季值序列yt进行平稳性检验.采用单位根检验，结果见表3，ADF=-1.221931，在显著性水平(1%～10%)下，大于ADF 临界值，且相伴概率为0.8979，充分说明该序列是非平稳的.

表3 我国国内生产总值时间序列平稳性检验

为了消除趋势并减小序列的波动性，对原序列取自然对数，并做逐期差分，通过分析比较最终选择做1阶逐期差分.从自相关与偏自相关分析图来看，序列的趋势基本消除，但当k=4，k=8时，样本的自相关系数和偏自相关系数显著不为0，表明季节性存在，继续做一阶季节差分.从表4的计算结果可以看出我国国内生产总值取对数差分后的时间序列通过了平稳性检验，且序列通过0均值检验.说明原始序列通过取对数，1阶逐期差分和1阶季节差分后可以建立ARMA模型，即可建立ARIMA(p,1,q)(P,1,Q)4模型，模型阶数需要综合平稳化序列的自相关和偏自相关图以及评价准则来选择.

表4 我国国内生产总值取对数差分后时间序列平稳性检验

3.4.2 模型的识别

通过观察平稳序列的自相关和偏自相关结果来帮助选择模型阶数，建立合适的模型进行预测分析，平稳化序列的自相关和偏自相关结果如图2所示.

图2 我国国内生产总值平稳化后自相关偏自相关图

结合自相关和偏自相关分析，考虑模型形式分别为ARIMA(2,1,3)(1,1,1)4和ARIMA(2,1,3)(2,1,2)4，同时ARIMA(2,1,3)(2,1,2)4模型又具体考虑了两种情况.

3.4.3 模型的建立与选择

由计算结果可知，三个模型都满足平稳可逆条件.将三个模型的参数估计和相关检验结果汇总列入表5和表6.

表5 不同ARIMA模型参数估计结果

表6 不同ARIMA模型检验结果

另外，模型的残差序列通过检验.比较表中各个模型的检验结果，第三个模型的AIC和SC较小，不管是样本期内还是样本期外的MAPE值显示其预测精度最高.因此选择第三个模型比较合适，其展开式为

(1+0.7609B4+0.1174B8)(1-0.3053B-0.6783B2)(1-B4)(1-B)ln(yt)

=(1-0.6302B+0.6432B2+0.9840B3)(1+0.0148B4+0.9447B8)εt.

3.4.4 预测

4 模型结果比较分析

为了比较四种模型的预测效果，笔者将真实值与四种模型预测结果绘制成下面图3，Y表示GDP时间序列，YF1表示温特线性和季节性指数平滑模型预测结果，YF2表示季节性交乘趋向模型预测结果，YF3表示含虚拟变量回归模型预测结果，YF4表示ARIMA模型预测结果.从图3来看，四个模型整体预测效果较优.对于样本期外的预测，从图形来看预测误差较大的时间点是2020年第1季度，这由于新冠肺炎疫情突发事件的影响，导致预测误差偏大.但同时也看到了，疫情虽然短期会对经济造成重大冲击，但是并不会改变中国经济长期向好的根本趋势.

从图3中很难定量比较四个模型预测结果的差别，为了精确比较差异，将数值结果汇总至表7.由于不同的模型建模会存在初值问题，差分问题，因此会有部分样本数据损失.这里为了方便比较，将样本期内时间段统一为2004年第1季度至2018年第4季度.样本期外仍然统一为2019年第1季度至2020年第4季度.

图3 我国国内生产总值四种模型预测结果

从表7中的数据可以看出，从样本期内拟合效果来看，ARIMA模型最优，温特线性和季节性指数平滑模型次之，季节交乘趋向模型和含虚拟变量回归模型拟合效果相对差些.但是从样本期外预测效果来看，含虚拟变量回归模型预测效果最好，温特线性和季节性指数平滑模型次之.四种模型预测结果存在差异，但整体效果较优.

表7 四种模型预测结果比较分析

为了分析2021年各季度GDP的发展状况，进一步对2021年四个季度GDP进行预测，数值结果见表8，可以看出未来我国国内生产总值仍然是保持稳步增长态势.

表8 2021年我国国内生产总值四种模型预测结果(亿元)

5 结 论

本文以我国国内生产总值时间序列为研究对象，重点探究季节性时间序列的建模方法，从定量的角度分析我国国内生产总值的变化趋势，以及对未来的发展预测分析.结果表明四种模型整体对我国国内生产总值的预测效果较好.但2020年第1季度预测结果偏差较大，这主要是因为新冠肺炎疫情突发事件的影响，从而说明对于突发事件预测也是无能为力.虽然疫情短期对经济造成重大冲击，但并不影响中国经济长期向好的基本面.比如从ARIMA 预测结果来看，2021年GDP将增长8.1%.预测结果支持2021年3月5日李克强总理作政府工作报告中2021年国内生产总值增长6%以上的预期目标.在教学过程中，适时开展思政教育[10]，引导学生用全面、辨证、科学、长远的眼光看待我国的经济发展，坚定信心，激发学生学以致用、科技报国的家国情怀和使命担当.

通过综合案例分析，培养学生运用统计软件在数据收集、数据整理、数据分析等方面的操作技能.培养学生深入理解统计建模思想，提升统计思维.统计预测建模是建立在数据的基础上的，是通过数据进行推断的，因此教学过程中要教育学生树立正确的统计责任意识，严肃认真、实事求是.统计建模允许人们根据自己的理解提出不同的预测方法，因此统计建模对结果的判断原则不能是“对”或“错”，只能是“好”或“坏”，在教学过程中要强调统计方法的选择与优化，培养学生精益求精的工匠精神.

本文采用的是传统的季节性时间序列建模方法，模型易于理解而且预测效果较优.在建模过程中也尝试使用BP神经网络方法[9]，但是从预测结果来看，该方法对于样本期内预测效果较优，但是样本期外预测精度不高.在不断探索优化的过程中，激发学生学习兴趣，鼓励尝试创新组合预测模型[8-9,11]、周期ARMA模型[12]等，提高课程学习的创新性和挑战度.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.