关于三角形内特殊点的几何不等式

安徽信息工程学院 (241000)

李冠戬

1.引言

几何不等式是沟通代数与几何的重要媒介，它既有几何的直观形象，又有代数的逻辑严密.文[1]讨论了关于三角形内一点作三边对称点得到新三角形的方法.本文借鉴这种方法，分别取该点为外心，垂心，内心，重心，费马点和勃罗卡点，得到一系列优美简洁的表达式，并研究它们之间的不等关系，推导出一个新的几何不等式.

首先，介绍一个定理，它是我们一切思路的源头.文[1]第98页例6中证明了如下定理：

定理1P为△ABC内一点,点P关于边AB,BC,CA的对称点分别为P1,P2,P3,则

(2)∠P1P2P3=∠BPC-∠A,∠P1P3P2=∠CPA-∠B,∠P2P1P3=∠APB-∠C.

2.外接圆半径的表达式

在这个定理的基础上，我们分别取P为△ABC的外心，垂心，内心，重心，费马点和勃罗卡点，得到关于外接圆半径的表达式.

以下是一些必要的符号和记号.

定义△ABC中，记AB=c，BC=a，CA=b，S,R，r，C，p分别为其面积，外接圆半径，内切圆半径，周长及半周长，O，H，I，G，F，P分别为外心，垂心，内心，重心，费马点和勃罗卡点，记它们关于三边的对称点构成的三角形面积分别为SO,SH,SI,SG,SF,SP,外接圆半径分别为RO,RH,RI,RG,RF,RP.

于是有下面几个定理成立.

定理2.1 外心O关于三边的对称点构成的三角形与原三角形全等.

证明:当P为外心O时，PA=PB=PC=R,∠APB=2∠C,∠BPC=2∠A,∠CPA=2∠B.则由定理1得P1P2=b,P2P3=c,P3P1=a,∠P1P2P3=∠A,∠P1P3P2=∠B,∠P2P1P3=∠C.故此时△P1P2P3与△ABC全等，原命题得证.

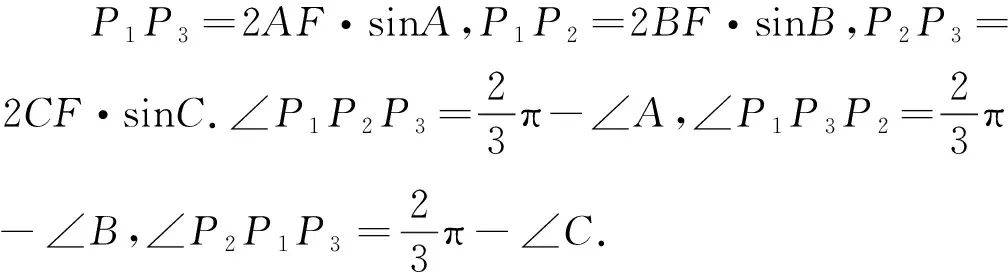
(注：证明中用到AH=2RcosA,AI=

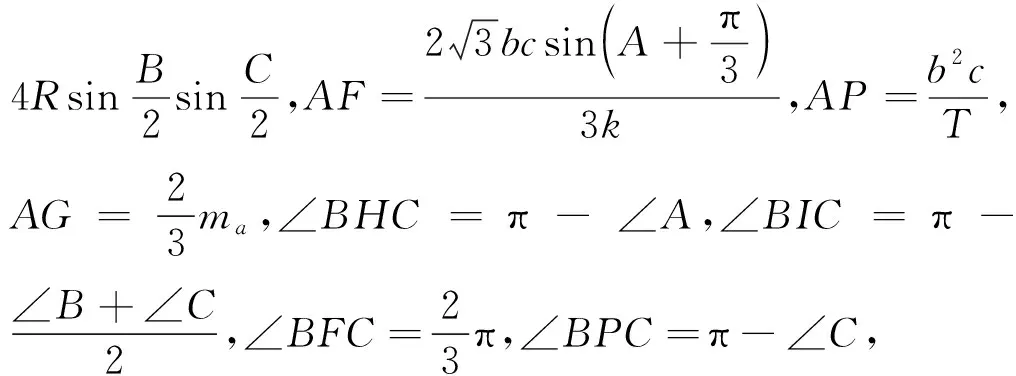
3.两个引理

为了证明将要给出的几何不等式，我们先证明两个引理.

引理1 (Gerretsen不等式)设R，r，p分别为△ABC的外接圆半径，内切圆半径，半周长，则16Rr-5r2≤p2≤4R2+4Rr+3r2.(2)

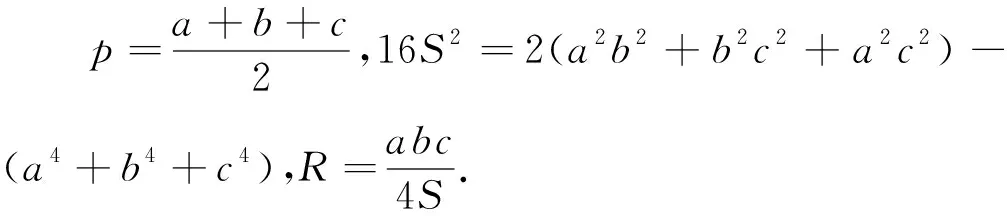
4.新的几何不等式

根据定理2.1和定理2.2，我们推导证明出如下的几何不等式.

定理3RI≤RF≤RH,RI≤RP≤RH，RI≤RG≤RH.(4)

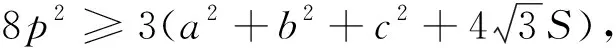
再证RI≤RG，由定理2.2等价于证明3r∑a2≤4mambmc.

最后证RG≤RH,由定理2.2等价于证明8mambmc≤3R∑a2.