对一道几何最值问题的探究*
2023-01-12安徽省合肥市第一中学230601
安徽省合肥市第一中学 (230601)
涂成浪 谷留明(指导教师)
一、初识题目

图1
题目在矩形ABCD中,AD长为3,AB长为4,动点E在矩形ABCD的四边上运动,如图1,求点E到点A和点B的距离之和的最大值?
初看这道题时,以为只需简单地作一个对称,再利用三边关系求解,但发现此题求的是最大值,并非常见求最小值问题.经过简单的分析,容易确定所求线段和最大时,点E应在线段CD上,下文中只分析这种情况,且点E不在线段CD两端.根据直觉,觉得当点E应该在与点D或点C重合时,所求线段和取得最大值.
为了严谨地求出最值,先利用函数来对线段和进行表达,然后求出它的最大值.

二、讨论交流

图2
经讨论之后便出现了两种简单且巧妙的方法.我们从几何角度来考虑这个问题的.下面只分析点E在线段AB上(不含两端)时的情况,证DA+DB>EA+EB.
方法一:如图2:作点A关于点D的对称点F,连接BD,FE.延长BE交DF于点G.此时,DA+DB=FD+DB=FG+GD+DB>FG+GB=FG+GE+BE>FE+BE=EA+EB.
运用此法,可以证明随着点E从线段AB中点向点D靠近时,EA+EB逐渐变大.当点E与点D或点C重合时,EA+EB取到最大值8.
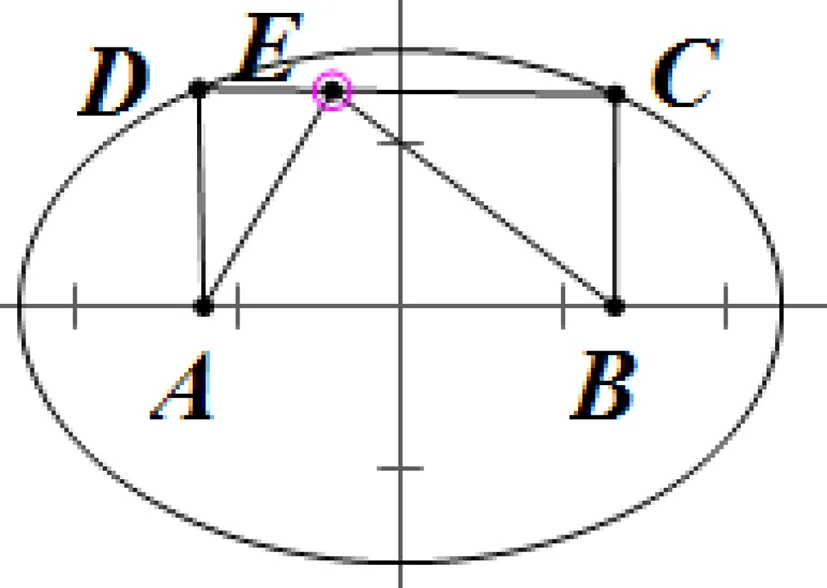
图3
方法二:如图3,构造一个以点A,B为焦点,长轴长为DA+DB=8的椭圆,在上半椭圆上取点D,C,使四边形ABCD为矩形.结合图形得线段CD上两点之间的点都在椭圆内,所以EA+EB<8=DA+DB.故当点E与点D或点C重合时,EA+EB取到最大值8.
以上两种方法都是从几何角度来思考这个问题的.方法一从三边关系来证明不等式,方法二构造椭圆,利用椭圆的第一定义来转化边,类似于根据点在园内,得到该点到圆心的距离大于半径.
三、“自我斗争”
虽然以上两种几何方法已得出结果,是否可将代数与几何相结合来解决这个问题?于是经过一番思索,我得到了以下数形结合的方法.
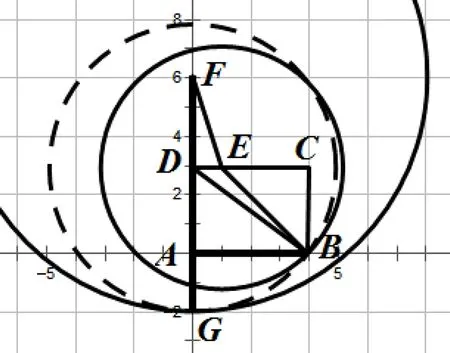
图4
目标是证明DA+DB>EA+EB,即证FD+DB>FE+EB,即证FG>FE+EB.如图4建系,设E(a,3)(0 相比于一般求最值的题目,本题难点在于求两条线段的和,这个方法的基本思路在于用圆的半径等长,将折线段转化为一条直线段,然后将要证的大小关系,转化为两圆的位置关系.
