变中有定，“揪”其根本——以一道高三解析几何调研题为例

江苏省锡山高级中学 (214174)

陈 敏

一、引言

一题多解和多题一解是数学解题教学常用的教学方法.数学解题方法一般分为通法与巧法,通法着眼基础，巧法着眼提高.通法是巧法的基础，巧法是通法的升华.在目前的数学解题教学中，一方面，一些教师对通法推崇有加，而对巧法敬而远之，甚至谈“巧”色变，学生习惯于套用解题的固有套路与程式，思维僵化而无创新色彩，“韧”性有余而“灵”性不足；而另一方面，一些教师片面追求巧法，轻视基础，缺乏对基本思想方法的挖掘与训练，有时甚至陷入对通法不屑一顾而巧法又一时想不起的尴尬境界[1].当然，既要注重基础，守住通法，又适时适度个性创新，催生巧法，“通”“巧”结合，“韧”“灵”并举，这是我们解题教学的理想境界.但是这种鱼和熊掌兼得的教学如何把握谈何容易.笔者认为，无论通法还是巧法，变中还是有定的东西，仔细分析题意、提高目标意识、充分利用条件、寻找解题思路、综合灵活选择方法、解题后的总结与反思等等这些都是变中不变的的东西.在新情境下，选择恰当的数学思想方法解决新问题的必备品格和关键能力，这才是根本之本.解析几何问题一般通法与巧法变化比较多、运算量大，解题要求高，但是分析问题、解决问题的基本方向和基本思路是变中之定，数学解题就像数学本身一样，应当是自然的、清楚的、明白的.本文从一道高三解析几何调研题说起.

二、问题呈现

图1

三、思路分析

四、解题研究

(一)设线法

解题反思：反观整个解题过程，目标很清晰，点P在第四象限、A，C，P三点共线等隐含条件条件的运用很充分，方法选择也较为恰当.其中关键是利用割补的思想，把△PCD面积可以表示为△PBC与△DBC面积之差，以直线BP的斜率k为参数建立面积目标函数(也可以以直线AP的斜率为参数)，通过换元，利用基本不等式求出面积的最大值，解题过程中要注意k的范围以及换元基本不等式中等号成立的条件，否则，可以用函数的单调性来解决.

设线法是解析几何的通性通法，把直线方程与圆锥曲线方程联立，得到一元二次方程，在判别式△>0的前提下，应用韦达定理、中点坐标公式、弦长公式等设而不求的方法解决相关问题.这种方法趋于定式，易于理解、掌握和运用，但这种方法往往运算量大，在考试的环境下，学生常常欲进维艰，耗时费力.

(二)设点法

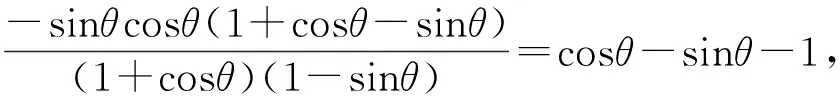
(三)动中有定

(四)变式研究

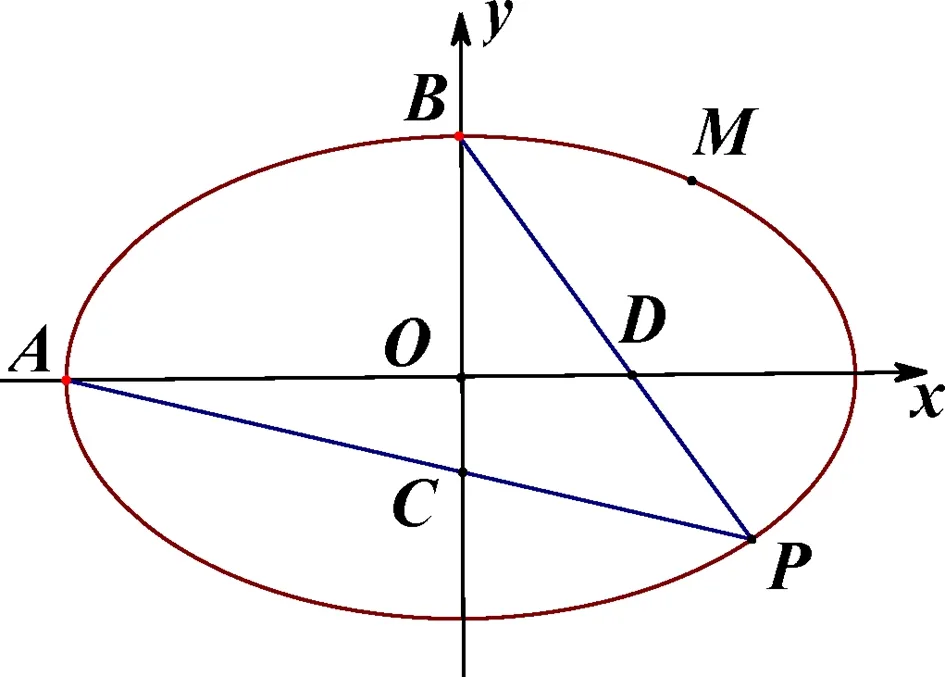
图2

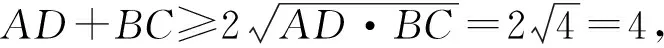
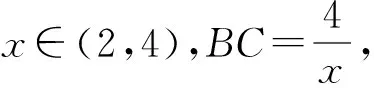
(五)转换他求

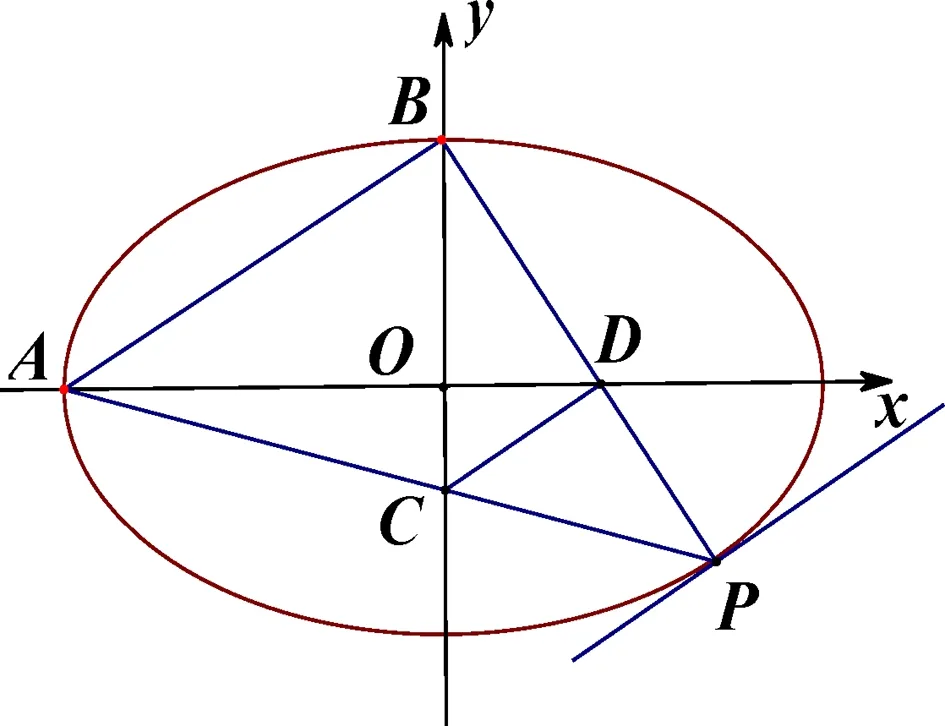
图3

2.判别式法：如图3，当与直线AB平行的直线与椭圆在第四象限相切时，点P到直线AB的距离的最大，此时点P就是切点.

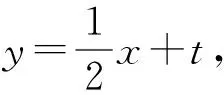
(六)回归课本

图4

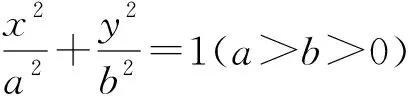
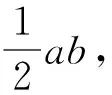
五、结语

以上对这道解析几何调研题的解析，我们主要用了基本不等式法、换元法、参数法、判别式法、数形结合法、线性规划法、导数法等思想方法，其中基本不等式法、换元法、参数法、判别式法属于代数法，数形结合法、线性规划法、导数法属于几何法，这些思想方法几乎涵盖了解析几何常用的思想方法.如何灵活选择恰当的数学思想方法，在新情境下解决新问题，这才是重要的，也是数学核心素养的根本要求.变中有定，“揪”其根本是实现这一根本要求的一条有效路径.这里变中之定，根本之本，一方面是指仔细分析题意、提高目标意识、充分利用条件、寻找解题思路、综合灵活选择方法、解题后的总结与反思等等这些都是多变解法中不变的的东西；另一方面是指课本，课堂教学应“以课本为本”.学好教材是高考取得好成绩的前提.我们要理解教材，“创造性使用教材”，而这样做的第一要义是理解数学：了解数学概念的背景，把握概念的逻辑意义，理解内容所反映的思想方法，挖掘知识所蕴含的科学方法、理性思维过程和价值观资源，学生养成良好的学习习惯，树立敢于质疑、善于思考、严谨求实的科学精神；认识数学的科学价值、应用价值、文化价值和审美价值.