图正则重加权稀疏约束的深度非负矩阵分解算法用于高光谱图像解混

蒋永丛， 何 飞

(1. 河南林业职业学院信息与艺术设计系，河南 洛阳 471002; 2. 郑州大学信息工程学院，河南 郑州 450001)

0 引 言

高光谱图像作为对地遥感观测的一种重要手段，在服务国防科技、农业发展、水资源监测、环境灾害等方面发挥着不可替代的作用[1-3]。但受限于有限的空间分辨率，高光谱图像中容易出现混合像元，即一个图像像元光谱是由一个或几个地物光谱混合而成[4-5]。高光谱解混是一种将图像混合像元分解成一组最纯的端元光谱和其对应的组成丰度的技术[6]。高光谱解混是解译高光谱图像的一种重要途径，因此对高光谱解混算法的研究变得格外重要。

当前高光谱图像混合像元分解算法可以大致分为三类。第一类是无监督解混算法，这一类算法从图像中提取指定数目端元，然后再采用全约束最小二乘算法估计端元对应的丰度。典型的算法包括顶点成分分析法（vertex component analysis, VCA ）[7]，空间能量约束的最大单纯形体积法（spatial energy prior constrained maximum simplex volume,SENMAV）[8]，空间单纯形加权端元提取法（spatially weighted simplex strategy，SWSS）[9]。第二类算法是有监督解混算法，这一类算法采用一个完备的光谱库作为字典，不对图像进行端元提取，仅需要估计图像混合像元的丰度成分。典型算法包括空谱加权稀 疏 回 归 法 （ spectral-spatial weighted sparse regression，SSWSR）[10]，光谱多视角协同稀疏回归法（spectral multiview collaborative sparse unmixing,SMCSU）[11]。第三类算法是基于非负矩阵分解（nonnegative matrix factorization, NMF）模型的无监督解混算法。这一类算法将高光谱图像分解成两个非负矩阵，即端元矩阵和丰度矩阵。由于NMF模型是非凸的，难以获得全局最小值。因此通常采用针对端元或丰度的先验知识来对模型施以约束以提升模型的求解精度。典型的基于NMF模型的解混算法包括有L1/2稀疏约束的NMF（L1/2constrained NMF, L1/2-NMF）[12]， 空 间 组 稀 疏 约 束 的 NMF（spatial group sparsity constrained NMF, SGS-NMF）[13]。

当前，在图像处理的研究过程中，深度学习范式越来越受到研究人员的关注，因为深度学习相比传统算法而言更加关注数据的隐层结构。为了使NMF算法也能获得学习隐层信息的能力，有研究人员提出了深度NMF算法，这类算法通过将端元矩阵经过多层分解以挖掘图像的深度信息。典型算法包括有多层非负矩阵分解算法（multi-layer NMF,MLNMF）[14]，稀疏深度非负矩阵分解算法（sparse deep NMF, SD-NMF）[15]。但这类算法仍然存在典型问题，即在深度分解的过程中无法有效地挖掘图像的先验信息以提升解混性能。

为了有效提升高光谱图像解混性能，提出了一种图正则和重加权稀疏约束的多层深度非负矩阵分解 算 法 （ graph regularized and reweighted sparsity constrained deep nonnegative matrix factorization,GRS-DNMF）。提出的 GRS-DNMF对传统 NMF模型分解得到的端元矩阵进行多层分解直至到达指定层数，并对各层中丰度矩阵同时施加图和稀疏约束以提升模型的鲁棒性。模拟数据集和真实数据集实验验证了所提出的GRS-DNMF算法相比其他算法具有明显解混优势。本文GRS-DNMF算法的核心创新点在于提出了一种对非负矩阵分解进行多层分解的深度模型且利用同时利用稀疏和图约束对多层丰度矩阵进行正则的方法。

1 光谱线性混合模型与非负矩阵分解算法

高光谱图像像元混合模型通常假定满足光谱的线性混合，表述如下：

式中： Y ∈ RB×N——包含个波段和个像元的高光谱图像；

M ∈RB×K——包含个光谱的端元矩阵；

A∈RK×N——个光谱的端元所对应的丰度矩阵；

E∈RB×N——噪声矩阵。

需要指出的是，线性混合模型通常需要满足两个本质约束项即丰度非负约束和丰度和为一约束。

非负矩阵分解算法是一种将多信号混合的数据分解成两个非负矩阵的乘积的一种有效方式。NMF通常表述如下的形式：

通过让上式分别对两个非负矩阵进行最小化优化，NMF算法可以有效求解两个非负矩阵，目标函数表述如下：

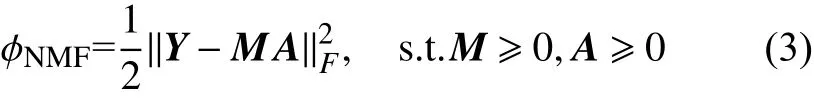
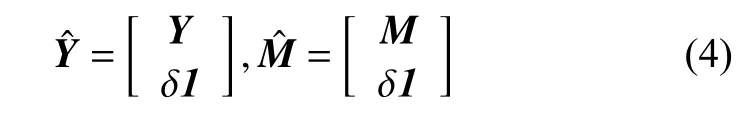
2 提出的图正则重加权稀疏多层深度非负矩阵分解算法

2.1 模型提出

为了有效提升NMF算法对高光谱图像的解混性能，提出了一种基于图正则和重加权稀疏约束的多层深度非负矩阵算法GRS-DNMF。对于多层深度非负矩阵算法，其第一层是将进行常规分解，形成和。第二层中，将第一层中的继续分解成和。这个过程将会重复继续下去，直至到达指定的层。对于多层深度非负矩阵模型，其最终的多层结构表述如下

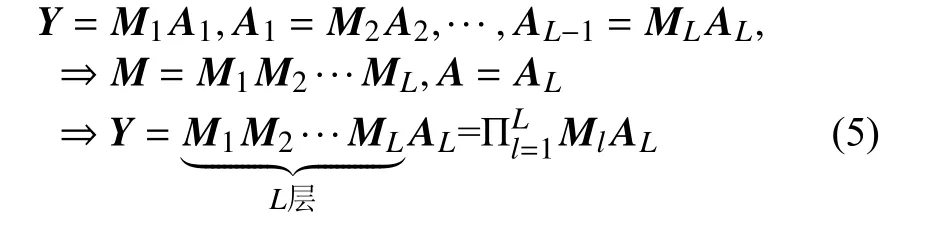
对于第l层，多层深度非负矩阵分解模块在该层的模型可以表述如下

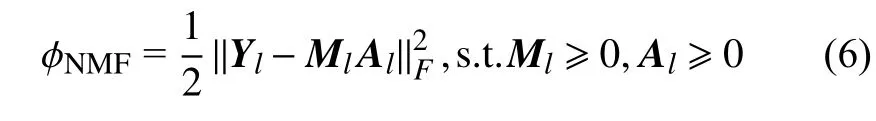
为了有效提升模型的鲁棒性，增强对高光谱图像的分解能力，本文采用图结构和重加权稀疏正则项对模型施以约束。为了有效挖掘图像和丰度矩阵在局部所具有的本质特征，即图像局部数据是空间光谱相似的，其丰度成分也应该是相近的。因此，通过获取图像局部数据的图结构并让其在丰度矩阵局部保持同样结构能有效提升丰度矩阵的估计效果。另一方面，丰度矩阵通常是表征图像中少量端元在混合像元时的成分。但事实上，对于混合像元而言，其通常由少量光谱混合而成，因此丰度矩阵呈现稀疏性。通常研究人员采用或稀疏项，但并没有稀疏，而相比是非凸的。为了避免和的问题，本文采用重加权稀疏正则项，通过引入权重矩阵来增强迭代优化过程中丰度矩阵的稀疏性。重加权同时具有的稀疏度和的凸结构。通过融合图结构和重加权稀疏正则项，在第l层的模型可以表述为

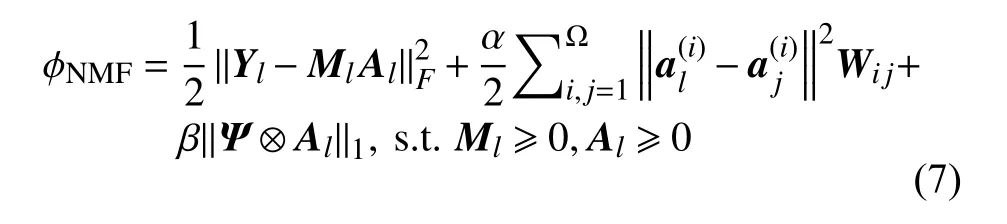
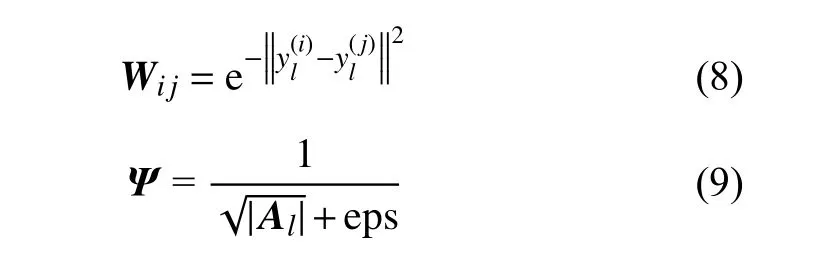
2.2 模型优化

为了方便模型的优化，首先将图正则约束项作如下改写：

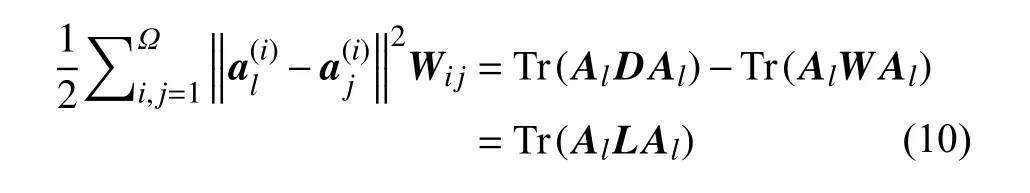
L=D-W——图拉普拉斯矩阵。

因此原始模型可以重新表述如下：

将非负和和为一约束写入模型，则拉格朗日函数可以表述如下

2.3 算法伪代码

为了有效阐述所提出的算法的求解流程，本文提供了算法的标准伪代码。伪代码如下所示：

3 实验结果与分析

3.1 实验评价方法

为了有效验证所提出的算法和对比算法在不同数据集上的有效性，本文采用两种典型的度量方法，即光谱角距离（spectral angle distance, SAD）和均方根误差（Root Mean Error Square）。SAD 度量原始光谱和从图像中估计出的光谱之间的光谱相似度，SAD值越低，表明两个光谱相关性高。和之间的SAD表述如下：

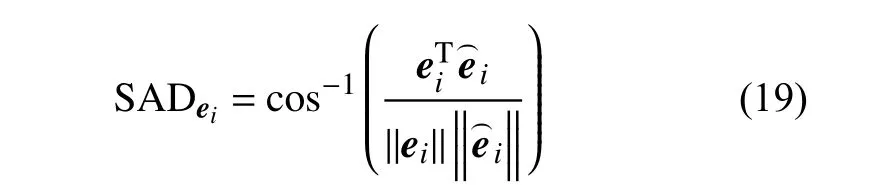
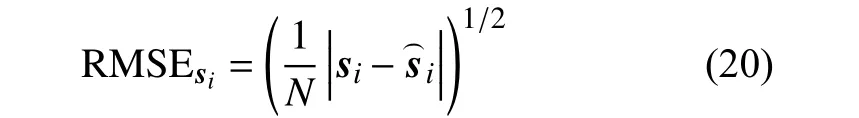
3.2 实验数据集

为了有效验证不同算法在不同场景数据集下的解混性能，本文采用两种数据集包括一种模拟数据集和一种真实数据集。模拟数据集由6种包含有224个波段的光谱按照一定比例混合而成。为了更好模拟真实的图像场景，不同信噪比(signal-tonoise ratio, SNR)的零均值高斯白噪声将会添加在模拟图像中，且丰度矩阵中像元最高的光谱纯度为0.8即图像中并不包含纯像元。模拟图像如图1所示。

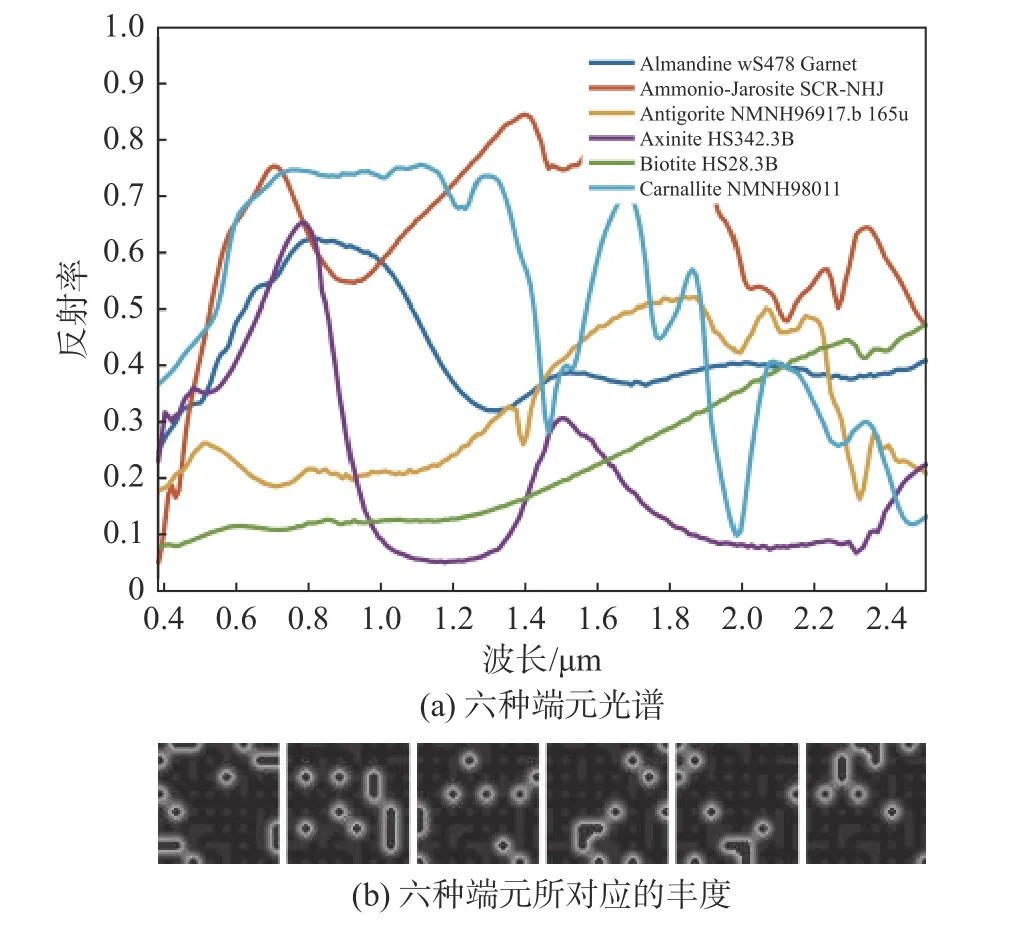
图1 模拟数据集

真实数据集采用高光谱解混标准数据集Cuprite，该数据集由机载红外成像光谱仪在美国内华达州Las Vegas地区拍摄。原Cuprite数据集尺度包含224个波段，考虑到水汽和噪声干扰，移除第1～6、105～115、150～170和 221～224波段，保留 182个波段。图像采用250×190×182大小的子图像作为实验数据集。采用端元数目估测算法对Cuprite数据集进行估测的端元数目为12。Cuprite数据集伪彩色图像如图2所示。

图2 Cuprite数据集伪彩色图像

3.3 对比算法与参数选择

为了有效验证所提出GRS-DNMF算法的有效性，采用3种标准算法进行实验对比，分别为端元提取算法VCA，L1/2-NMF算法和MLNMF算法。对于VCA算法，其是一种典型的无监督算法，仅需要输入图像矩阵和指定端元数目。对于L1/2-NMF算法，正则参数可以通过度量图像的稀疏度来确定。对于MLNMF算法，其涉及到对端元矩阵和丰度矩阵的稀疏约束和深度层的数目，这些参数分别设置为 3×10-5，7×10-5，10。

本文所提出的GRS-DNMF算法涉及到丰度的图和稀疏正则项以及深度层的参数。为了验证不同参数对模型解混精度的影响，分别将分别从1×10-5变化到 5×10-1，从 1×10-4变化到 5×10-1，层数 l 从1变化到10。如图3～图5所示，当，和层数 l分别设置为1×10-1，1×10-2，3 时 GRS-DNMF能产生最优解混结果。

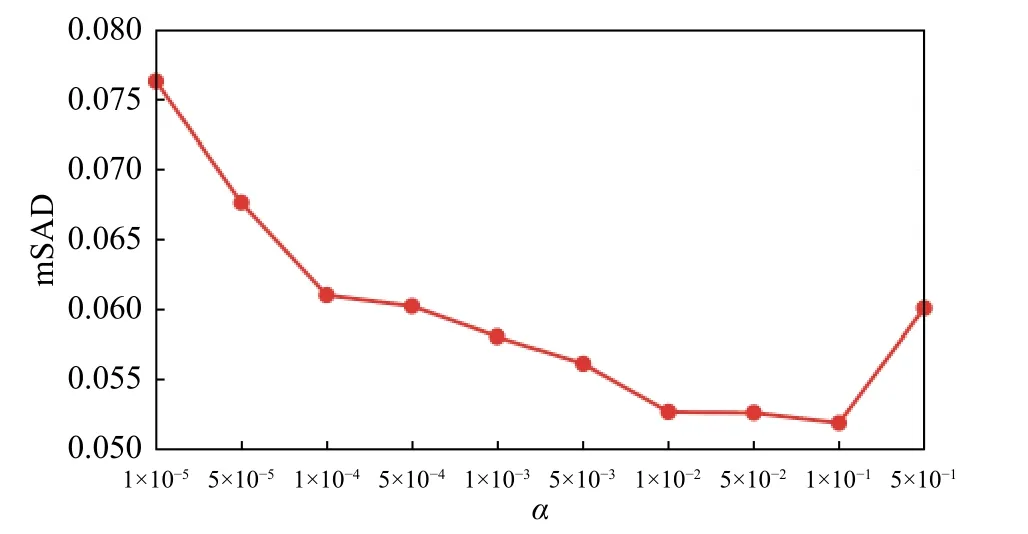
图3 GRS-DNMF算法在不同的平均SAD值

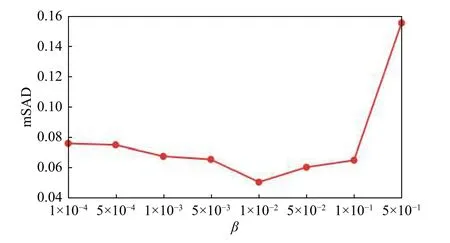
图4 GRS-DNMF算法在不同的平均SAD值

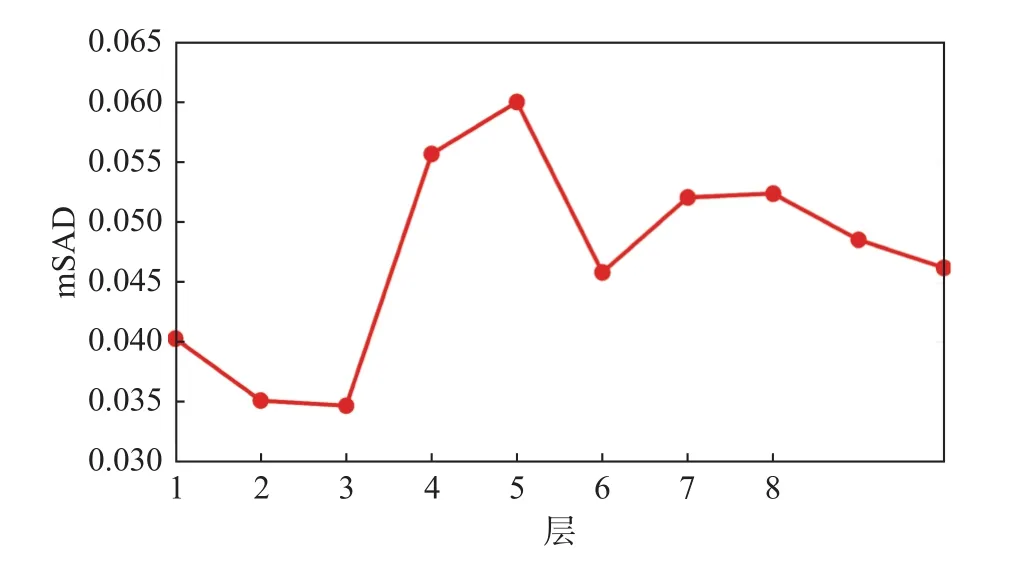
图5 GRS-DNMF算法在不同层的平均SAD值

3.4 噪声水平对算法解混精度的影响

为了度量所提出的算法和三种标准对比算法在不同信噪比情况下的端元提取精度，本试验对模拟数据分别添加15 dB至45 dB的零均值高斯噪声。图6展现了四种算法在不同信噪比下的端元提取平均SAD的变化趋势。如图所示，随着噪声的减弱，所有算法能逐渐获得较好的端元提取性能。但相比其他算法，本文所提出的算法无论是在噪声强度大的情况下还是在弱噪声的情况下均能获得最优的端元提取精度。

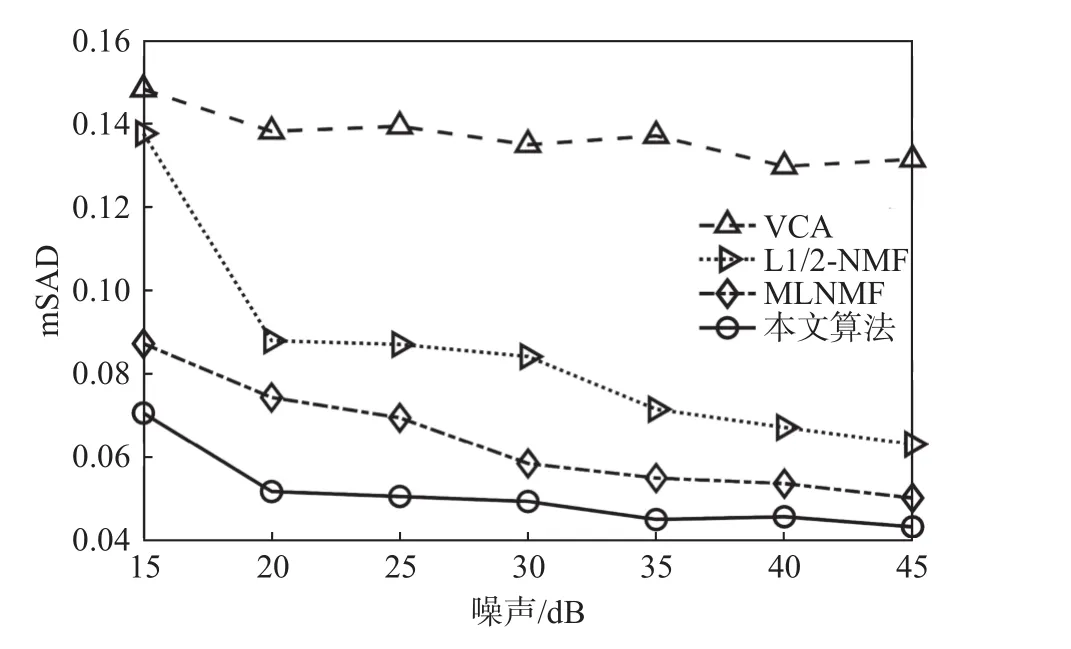
图6 四种算法在不同SNR下的平均SAD值

3.5 不同算法对图像的解混性能评价

为了度量所提出的算法和三种标准算法在模拟数据下提取端元的精度，本文考虑了在30 dB噪声的模拟数据下的算法性能对比。表1展现了四种算法在包含了6种端元的模拟数据集下的端元提取精度。从表中可以看出，对于6种端元，所提出的算法能准确地对其中三种端元进行估计并且能提供最小的平均SAD值，而MLNMF和L1/2-NMF算法则分别能提供对另外两个和一个光谱的准确度量。表2展现了四种算法在模拟数据集上对6种端元所对应的丰度进行估计的结果。与表1所呈现的结果类似，对于三种端元所对应的丰度而言，其依然能提供最优的丰度估计结果以及最小的平均RMSE值。实验证明所提出的算法相比其他算法在高光谱解混的任务中，能提供更优异的解混精度。

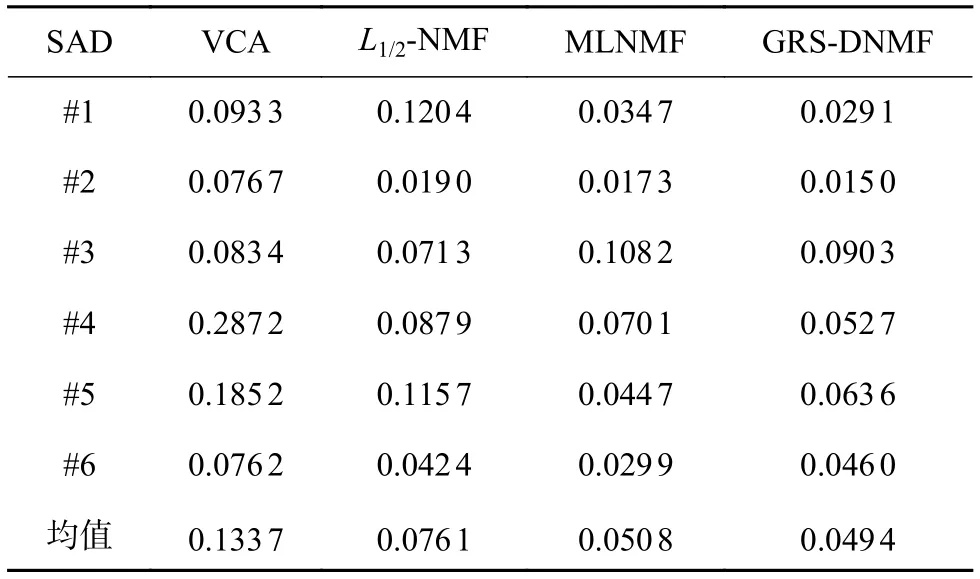
表1 不同算法提取6种光谱的SAD值和平均SAD值

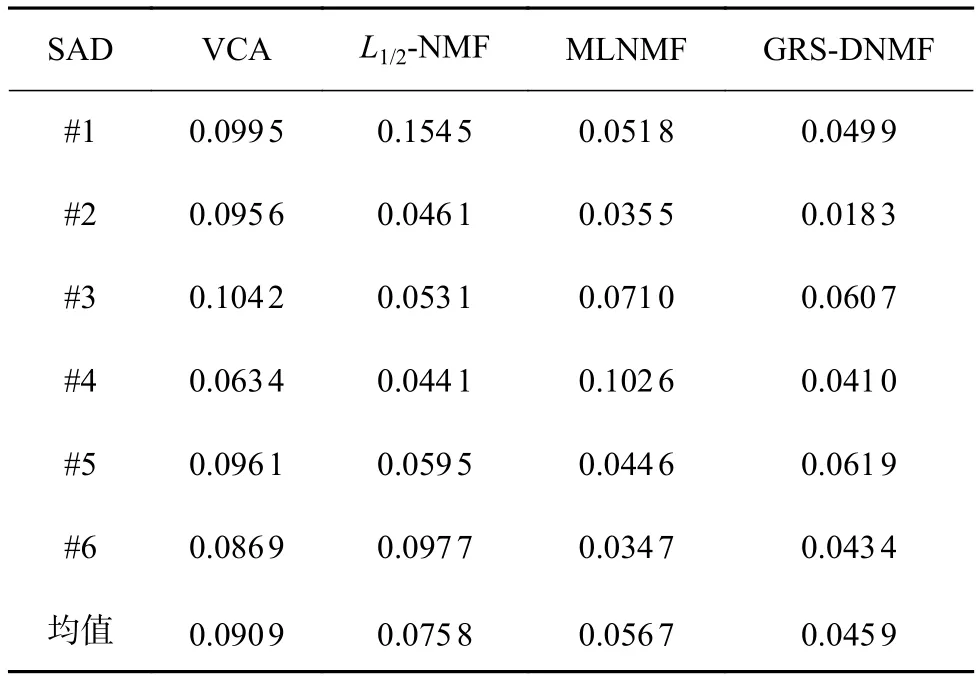
表2 不同算法提取6种光谱的RMSE值和平均RMSE值

3.6 算法解混效果的可视化评价

为了可视化地展现所提出的算法在30 dB噪声下进行解混任务后的光谱曲线，图7展现了6幅由算法提取的光谱和真实光谱可视化对比的图像。由图7可以观测出，对于真实光谱而言，由算法所提取的光谱具有较好的拟合效果。同时，为了可视化展现算法在不同噪声情况下估计的丰度和真实丰度之间的差异性，算法在 15 dB、25 dB、35 dB、45 dB噪声的模拟数据下进行了解混任务并进行丰度对比。图8展现了丰度对比图，相比真实丰度，在高噪声的情况下，算法所估计的丰度虽然能较好地恢复出真实丰度但一定程度上仍然受噪声的影响，如在15 dB情况下。但在噪声略微减弱的情况下，如25 dB到45 dB，算法则能完整恢复出真实丰度。

图7 GRS-NMF 算法提取的 6 种端元（点划线）和真实端元（实线）的可视化对比

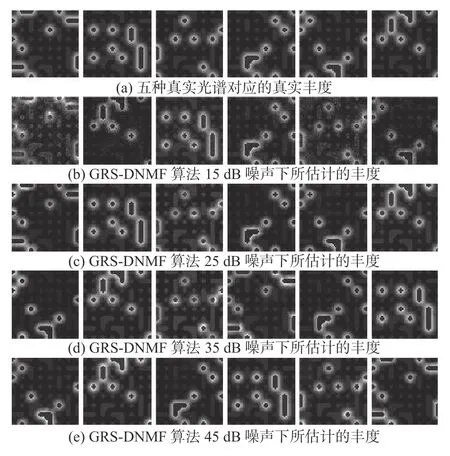
图8 GRS-NMF 算法在不同噪声下估计的丰度和真实丰度的可视化对比

3.7 不同算法在真实数据集上的解混效果

本试验是为了衡量不同算法在地物混合更加复杂的Cuprite数据集下的解混精度。表3展现了4种算法提取12种地物的SAD数值。如表3所示，在更为复杂的Cuprite数据集下，所提出的算法依然能准确地估计出5种地物的光谱，紧接着的是L1/2-NMF算法，其能对4种地物光谱进行估计，而MLNMF和VCA则分别能获得2种地物和1种地物的最优光谱估计性能。此外，所提出的算法对于12种地物能获得最低的平均SAD值，这证明了该算法具有较强的鲁棒性。图9可视化地展现了提取的12种光谱和光谱库之间的对比。由图可知，由算法提取出的光谱基本上匹配了标准光谱库光谱。此外，图10展现了算法分解出的12种矿物所对应的丰度。

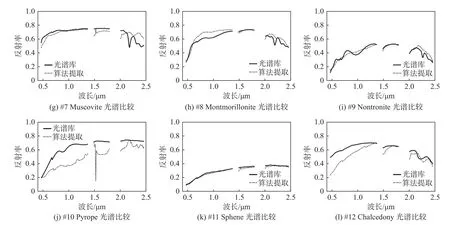
图9 GRS-NMF 算法在 Cuprite 数据集上提取的 12 种端元（点划线）和真实端元（实线）的可视化对比

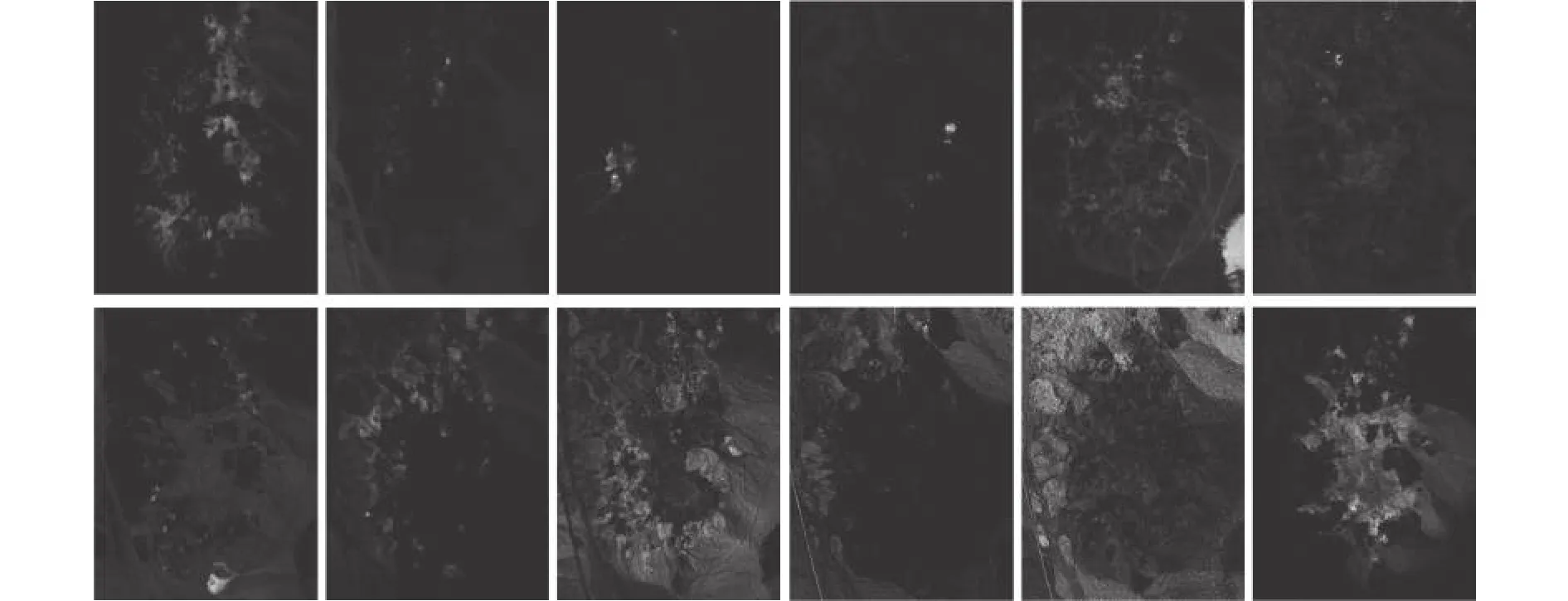
图10 GRS-NMF算法在Cuprite数据集提取的12种丰度的可视化展示

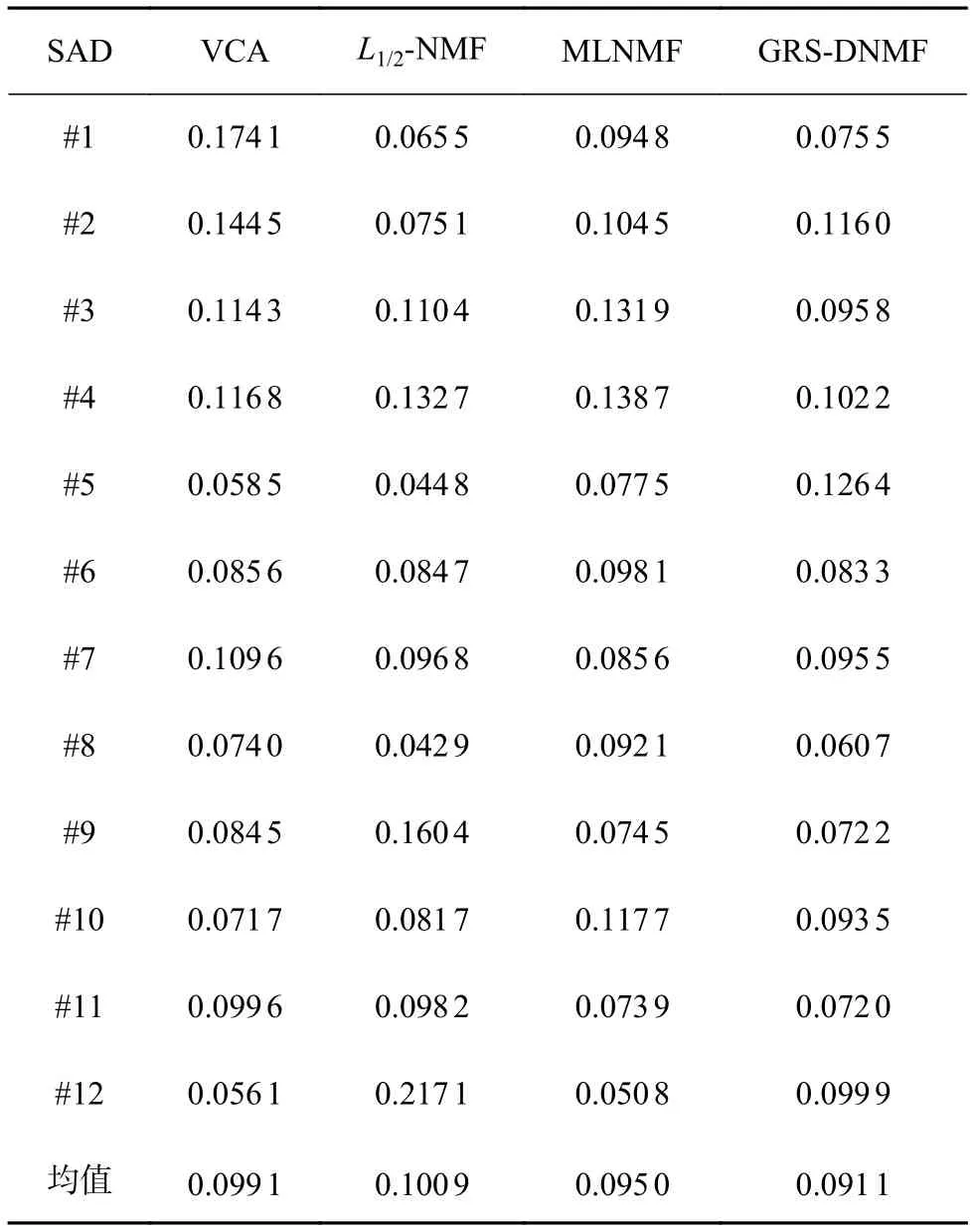
表3 不同算法提取6种光谱的SAD值

4 结束语

为了有效提升目前高光谱解混算法对高光谱图像解译的水平，提出了一种图和重加权稀疏正则的多层深度非负矩阵分解算法。该算法对端元矩阵进行多层的分解并对相对应的丰度矩阵施加图和稀疏约束直至分解至指定层数。在模拟数据和真实数据上的解混实验对比中，所提出的算法相比其他算法具有更明显的鲁棒性且能有效提升高光谱图像的解混能力。实验证明，所提出的算法在未来可以有效应用于国防科技领域，成为一种有效的对地观测手段。