分布式光纤裂缝监测实验与数值分析

赵丽芝， 唐福建， 周 智

(1. 大连理工大学建设工程学部土木工程学院，辽宁 大连 116024; 2. 海南大学土木建筑工程学院，海南 海口 570228)

0 引 言

外部荷载和周围环境作用会使建筑结构出现裂缝，为外部腐蚀物质进一步深入结构内部提供条件，从而加速结构破坏进程[1]。裂缝的早期监测可以保证结构的及时检修，从而避免严重的后果[2]。因此，裂缝的精确定位和裂缝宽度的评估对结构的安全运行具有重要意义[3-4]。

与声发射技术[5-6]、电子传感器[7-10]以及数字图像相关[3,11-12]等监测技术相比，光纤传感器具有体积小、质量轻、耐腐蚀、不受电磁干扰等突出特性，已经被广泛用于结构健康监测[13-14]。光纤光栅通过测定特征波长的漂移实现对基体局部应变的监测[15-16]。此外，基于布里渊的传感器，包括BOTDR和BOTDA技术，也出现在结构健康监测中[17-18]。然而，这些监测技术的空间分辨率较低，难以准确定位微裂缝和测量裂缝宽度。近年来，光频域反射仪(OFDR)技术使得利用分布式光纤传感器精确测量裂纹和量化损伤成为可能[19-21]。田昊等[21]采用OFDR分布式光纤监测钢筋锈蚀导致的混凝土保护层开裂，探讨了不同混凝土保护层厚度下裂缝宽度和光纤应变峰值随钢筋腐蚀率的变化规律，指出环氧树脂保护层造成了裂缝宽度不能完全传递至光纤。因此，粘结层存在造成的传递误差须被进一步分析。

本文利用OFDR分布式光纤传感器对基体裂缝宽度变化进行监测，并建立与试验基体一致的有限元模型，将Cohesive单元嵌入模型中光纤与光纤涂覆层界面以模拟光纤-涂覆层界面滑移行为。将试验结果和有限元分析结果进行对比，验证引入界面滑移模型的可行性，并进行参数化分析。

1 试验研究

该实验采用分辨率为9.524 µm的可移动平台模拟工程结构中裂缝扩展过程。如图1所示，可移动平台分为左右两部分，平台材质为钢材，平台可通过两侧旋钮左右移动。该试验中，固定左侧平台，旋转右侧旋钮使得右侧平台向右移动，从而使得两平台之间的缝隙逐渐扩大，这一过程与结构中裂缝在外力作用下逐步扩张的过程相似。右侧旋钮每旋转一格，右侧平台向右移动9.524 µm的位移，认为该位移即为裂缝的宽度，同时记录此时的光纤应变。使用环氧树脂胶粘剂将分布式光纤固定在平台表面，光纤一端浸入光纤匹配膏中，另一端连接OFDR分布式光纤解调仪。本实验采用的分布式解调仪的分辨率为2.61 mm。为了研究粘结剂强度对光纤监测裂缝的影响，本文采用3种不同强度的粘结剂，通过纳米压痕仪测得3种粘结剂固化后的强度分别为 0.473 GPa (粘结剂#1)，2.035 GPa (粘结剂#2)和5.630 GPa (粘结剂#3)。

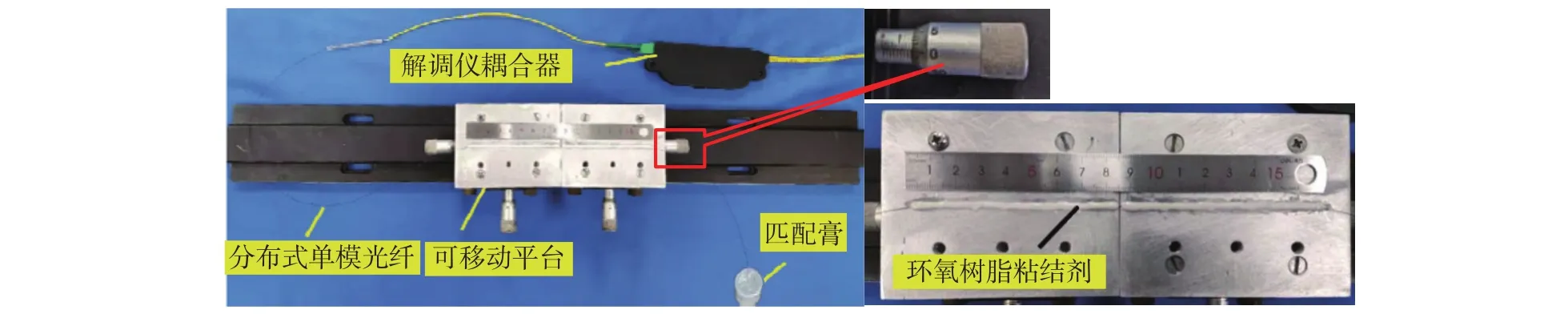
图1 OFDR分布式光纤监测裂缝扩展试验装置

采用3种不同强度粘结剂封装的OFDR分布式光纤的应变分布如图2所示。不同强度粘结层的光纤应变沿长度分布相似，即在裂缝处应变最大，并沿远离裂缝的方向逐渐减小，直至光纤末端应变降为零，呈现出中间大两头小的单峰状，且光纤应变最大处对应裂缝位置。当裂缝宽度超过30 µm时，峰值应变的增长速度明显减小，这种变化与中间层界面出现软化以及中间层进入塑性状态有关。38.096 µm裂缝宽度下3种粘结层的光纤应变峰值分别为 546.256 µε (粘结剂#1)，634.842 µε (粘结剂#2)和 650.685 µε (粘结剂#3)，可见光纤应变峰值随粘结剂弹性模量的增大而增大。

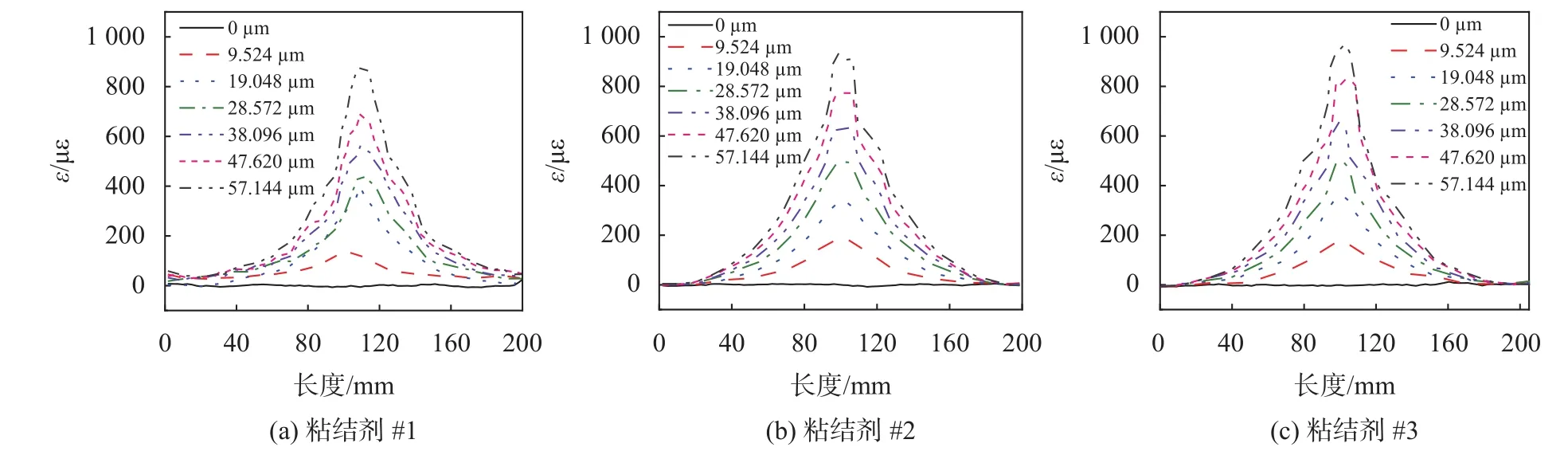
图2 OFDR分布式光纤沿长度的应变分布

2 分布式光纤监测裂缝应变传递理论

很多学者对分布式光纤监测基体裂缝时光纤应变分布函数模型进行了研究[17,22-23]，这些模型假设所有材料为线弹性材料，开裂基体为轴对称结构，裂缝位于对称轴处。基于剪滞理论以及变形协调方程，当基体裂缝宽度为w时，光纤沿长度的应变分布如下式所示：

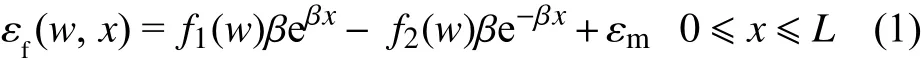
L——光纤粘结长度的一半。

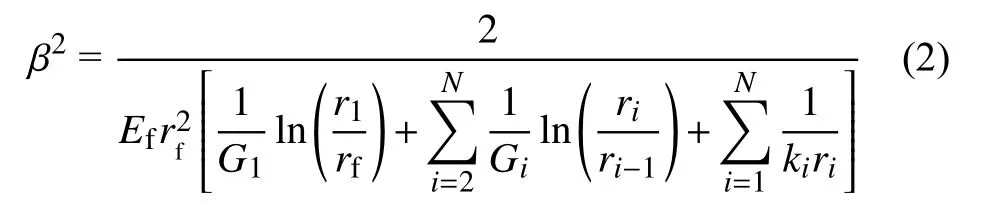
若光纤应变仅仅由裂缝扩展引起时，将式(2)和式(3)代入式(1)可以得到裂缝处(x=0)光纤应变，即光纤最大应变与裂缝宽度w的函数关系式为：

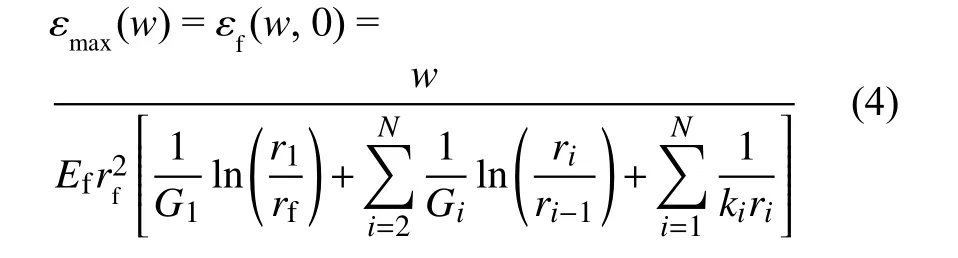
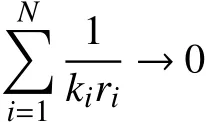
3 数值分析

3.1 有限单元模型

基于ABAQUS软件模拟了分布式光纤监测裂缝扩展的有限元分析模型。建立了与标定实验等比例的三维有限元模型，包括两块可移动钢材基体，分布式光纤和光纤粘结层，如图3所示。为了更好地模拟裂缝扩展，设置了合理的边界条件：允许基体构件沿z轴方向移动，其余方向固结；左侧基体沿z轴正方向移动0.25 mm，右侧基体沿z轴负方向移动，移动最大位移为-0.25 mm。

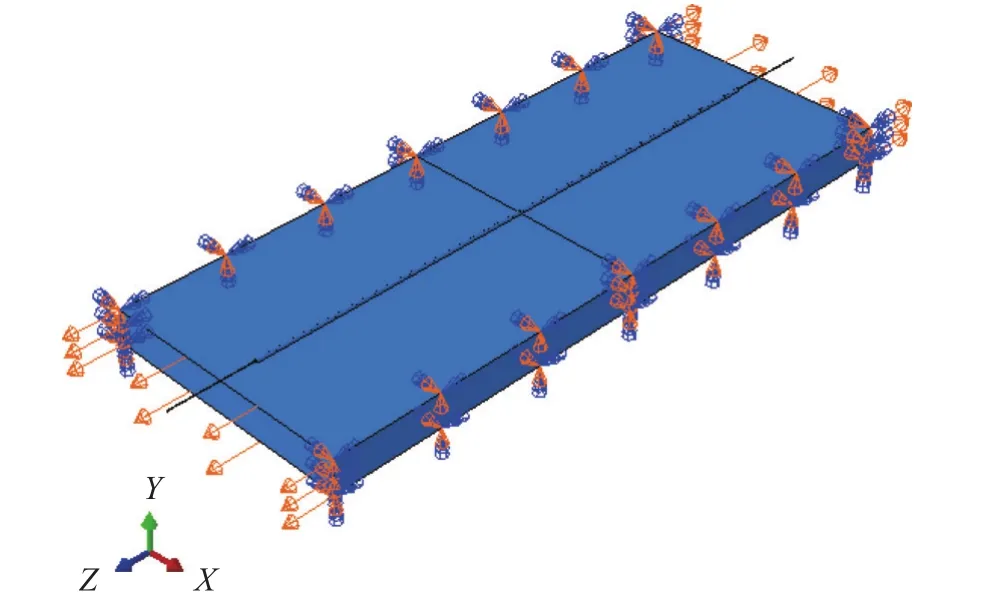
图3 有限单元模型

分布式单模光纤的截面示意图如图4（a）所示。单模光纤的纤芯直径为125 µm，涂覆层的直径为250 µm，假定粘结层上表面边界为抛物线形状。通过试验观察到，随着裂缝宽度增大，裸光纤逐渐从涂覆层中滑出，而其余界面几乎未观察到滑移，因此，在FEM中，假设基体-环氧树脂以及环氧树脂-光纤之间的界面粘结良好，将分布式光纤的涂覆层和光纤作为单独的部件构建，分别模拟了光纤与涂覆层之间完美粘结和两者之间存在界面滑移两种情况。光纤-涂覆层的界面滑移是通过在涂层与裸光纤的界面中插入零厚度的Cohesive单元来实现的，单元位置如图4（a）所示。Cohesive单元的性能由光纤拉拔实验得到。

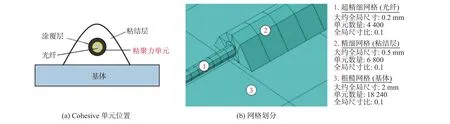
图4 有限元模型单元概况

经过网格敏感性分析，采用2 mm的粗网格对基体进行网格划分；环氧树脂粘结层采用精细化网格划分，局部尺寸大约为0.5 mm；光纤直径只有0.125 mm， 所以使用超精细化网格划分，光纤网格划分尺寸为0.2 mm。网格划分数量如图4（b）所示。被测基体、环氧树脂、涂覆层和光纤采用八节点六面体线性减缩积分单元(C3D8R)进行建模，光纤-涂覆层界面采用八节点内聚单元(COH3D8R)进行建模。

如图5所示，本文的Cohesive单元采用双线性粘结滑移模型[17]。根据剪应力和界面滑移量的变化趋势可将该模型分为弹性阶段、损伤演化阶段和脱粘阶段。在弹性阶段，光纤与涂覆层之间的剪应力与界面滑移位移呈线性关系，界面刚度为k。当剪切应力达到临界值τcr时，界面进入软化阶段。在这一阶段，界面局部滑移量增大，界面剪应力减小，这与界面刚度退化有关。随着界面相对滑移继续增大，光纤从涂覆层中滑脱，界面彻底失效，界面刚度减小为零。界面刚度k、临界剪应力值τcr和临界滑移量ss由光纤拔出实验确定，分别为12.11 MPa/mm，0.23 MPa和0.19 mm。FEM中假定构件材料均为线弹性材料，采用纳米压痕法测定了光纤、涂覆层和基体材料的弹性模量，分别为 72 GPa、1 GPa 和200 GPa，泊松比分别取 0.17，0.48 和 0.25。

图5 粘聚单元本构

3.2 FEM结果讨论

当假定光纤与被测基体中间各界面之间粘结完好时，光纤监测基体开裂的应变分布如图6所示。三种粘结剂封装下，光纤沿长度的应变分布呈现相同的规律，光纤应变集中在裂缝附近10 mm的范围内，距离裂缝10 mm以外的光纤应变基本为零，且光纤在裂缝位置处的应变最大。当裂缝宽度仅为29 µm 时，光纤应变最大值达到 7 040.051 µε (粘结剂 #1)，9 318.07 µε (粘结剂 #2)和 10 238.90 µε (粘结剂 #3)，是实际实验结果的20倍以上，因此，不考虑界面滑移的FEM光纤监测裂缝扩展模型无法用来模拟实际工程中光纤监测裂缝的过程。

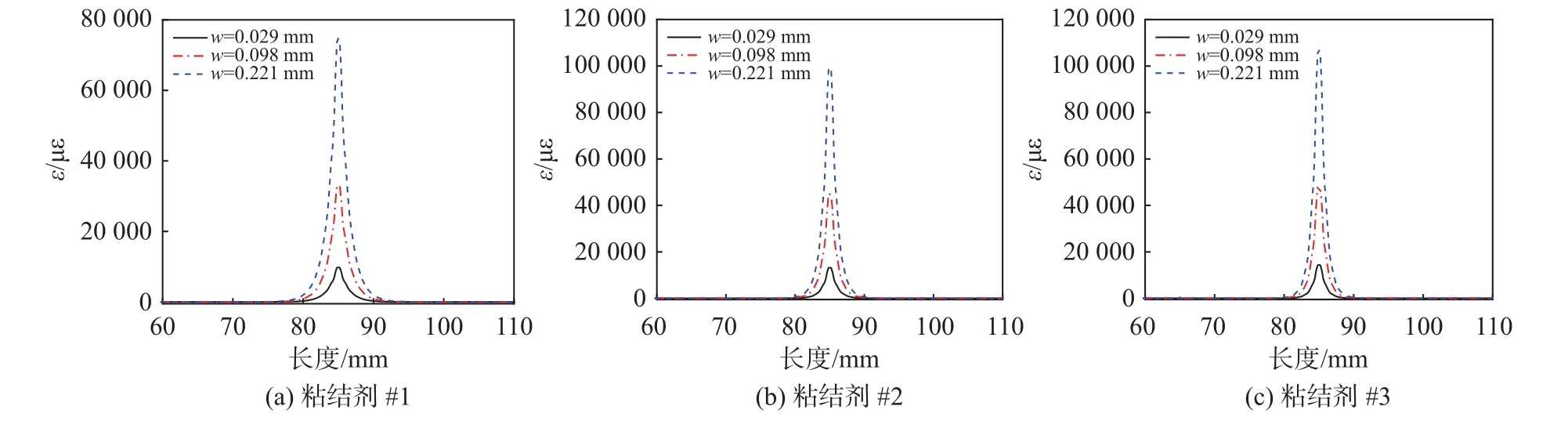
图6 界面粘结完好下光纤监测裂缝应变分布

图7为考虑界面滑移后，光纤监测裂缝的应变沿长度的分布规律。以粘结剂#1(图7（a）)为例，当裂缝宽度为58 µm时，光纤应变集中在距离裂缝30 mm的范围内，距离裂缝位置30 mm以外的光纤受到裂缝扩展的影响很小，应变接近于零。随着裂缝宽度扩大到209.60 µm时，光纤上各个点的应变都有大幅度增大，与图6不同处在于，光纤应变分布状态不止集中在裂缝附近，而是向裂缝两侧逐渐扩大。当裂缝宽度到达395 µm后，光纤峰值应变到达4 056.095 µε，此后，光纤应变峰值不再随着裂缝宽度的增加而增大，而是在裂缝附近出现平行于横轴的直线段，这是因为，当裸光纤从涂覆层中滑脱之后，光纤界面刚度为零，不再承受剪应力，脱粘部分的光纤只受到均匀轴向拉力。使用粘结剂#2(图7（b）)和粘结剂#3(图7（c）)作为光纤粘结层的光纤传感器呈现相同的应变分布规律。

图7 考虑界面滑移的光纤监测裂缝应变分布

将裂缝宽度为 100 µm，155 µm 和 182 µm 的有限元模拟结果与实验结果进行对比，如图8所示。从图中可以看出，考虑界面滑移的有限元的光纤应变分布与实验结果基本一致，在裂缝宽度为100 µm时，有限元的结果应变峰值大于实验结果，这种差异主要是由于环氧树脂与光纤涂覆层的材料性能，以及环氧树脂尺寸与光纤在环氧树脂中的位置沿粘结光纤长度不一致造成的。此外，环氧树脂与混凝土之间的界面并没有形成完美的粘结，也会影响开裂应变向光纤的传递。综上所述，本文提出的考虑光纤-涂覆层界面粘结滑移机制的有限元模拟方法更适合于分布式光纤传感器的裂缝监测。

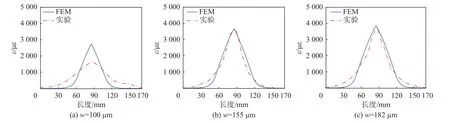
图8 不同裂缝宽度下实验与有限元光纤应变沿长度分布对比

图9为两种有限元模型下光纤应变峰值与裂缝宽度的关系，对于年平均相对湿度小于60% 地区一类环境的构件，最大极限裂缝宽度限值为0.4 mm，其余环境下，最大裂缝宽度限值则更低。因此，宽度大于0.4 mm的裂缝在本文不着重讨论。图9（a）是未考虑界面层滑移的有限元结果，光纤应变峰值εmax随着裂缝宽度w基本呈线性增加，这一结果与解析结果式(4)得到的结论一致。考虑界面滑移的有限元模型，当裂缝宽度小于0.322 mm时，光纤应变峰值随着裂缝的增大逐渐增大，但是增加速度越来越缓慢，这是因为光纤与涂覆层界面刚度k随着裂缝宽度w的增加而减小，且在裂缝附近的变化尤为显著。随着k值减小，相应的光纤界面剪应力减小，随之光纤应变峰的增长速度减慢，式(4)的分母不再为常数，所以光纤应变峰值与裂缝宽度关系不再线性相关。基于理论结果以及图9可知，考虑界面滑移后光纤峰值与裂缝宽度的关系与界面粘结完好的结果相似，不同之处在于刚度界面刚度降低导致光纤应变增长速度缓慢，因此，考虑界面滑移后光纤峰值与裂缝宽度的关系最可能满足指数小于1的幂函数。进一步对光纤应变峰值和裂缝宽度之间的关系进行幂函数拟合发现，在裂缝宽度未达到临界宽度0.322 mm之前，光纤应变峰值与裂缝宽度之间的关系满足指数为0.5的幂函数，且幂函数系数与中间层材料属性相关，函数关系式如图9（c）所示。

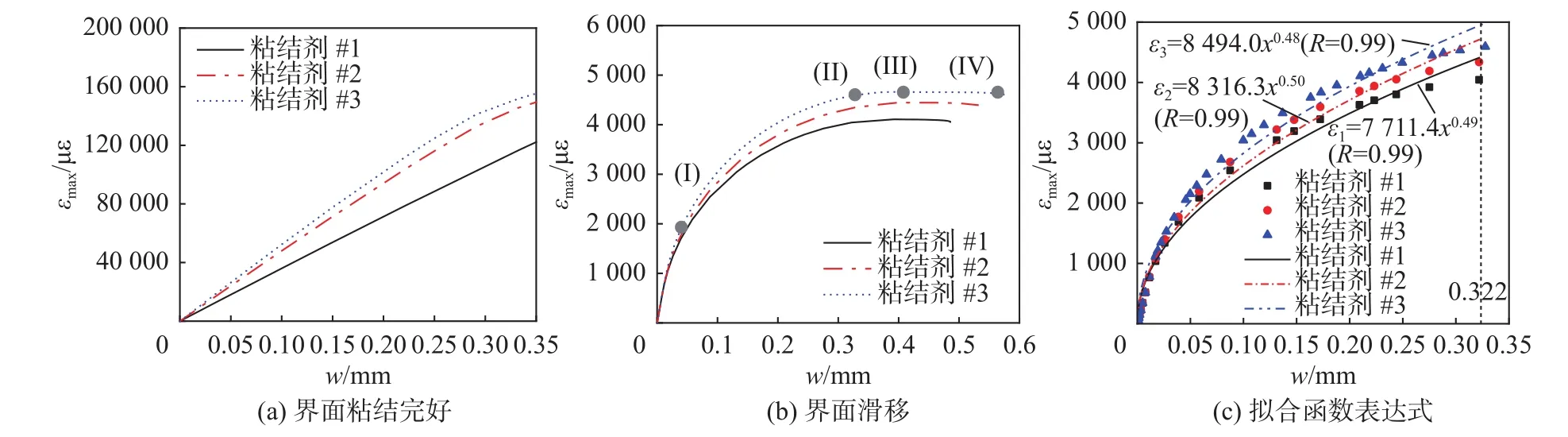
图9 光纤应变峰值与裂缝宽度关系

当裂缝宽度大于0.322 mm后，光纤应变峰值不再增大，基本保持为恒定量，如图9（b）所示。这是因为当裂缝宽度大于0.322 mm后，裂缝附近的界面基本失效(图10（b）)，界面滑脱，界面剪应力为零，因此光纤斜率为零。从图9中还可以观察到，不论是哪一种界面类型的有限元模型分析结果，封装光纤的粘结层弹性模量越大，相应的光纤应变峰值也越大。幂函数的指数与界面参数相关，幂函数系数与中间层材料参数相关，本文中3种强度粘结层的拟合相关性均为99%。

图10 为图 9（b）中点 (I)、(II)、(III)和 (IV)对应的粘聚力单元的尺寸刚度退化 (SDEG)云图。这4个点分别代表光纤涂覆层界面的不同阶段：第1个点是界面处于软化区域阶段，此时对应的裂缝宽度为58 µm，第2个点处于界面局部失效的临界位置，对应的临界裂缝宽度为0.322 mm，第3个点对应于界面局部出现滑脱行为，裂缝宽度为0.402 mm，第4个点对应的裂缝宽度为0.578 mm，此时界面出现大面积滑脱。在（I）点处，光纤的应力较大的地方出现在裂缝附近，且应力最大值为168.4 MPa，此时，裂缝附近的界面处于软化阶段，没有发生滑脱，SDEG值小于 1，最大值为0.82，位于距离裂缝0.3 mm处，而非裂缝处。当裂缝宽度增加至0.322 mm时，界面的Cohesive单元SDEG最大值为0.996，也就是说界面即将出现滑脱现象。当裂缝宽度增加至（III）点，距离裂缝 12～14 mm 处的Cohesive单元消失，说明该位置处光纤-涂覆层界面最开始出现脱粘，相应于该点的光纤应力大小为330.4 MPa。如图 10（d）所示，裂缝宽度增大到0.578 mm 时，距离裂缝 10～20 mm 处的 Cohesive 单元消失，裂缝附近的Cohesive单元虽然没有消失，但是SDEG值均接近于1，临近失效状态；裂缝附近光纤正应力值仍然为330.4 MPa。

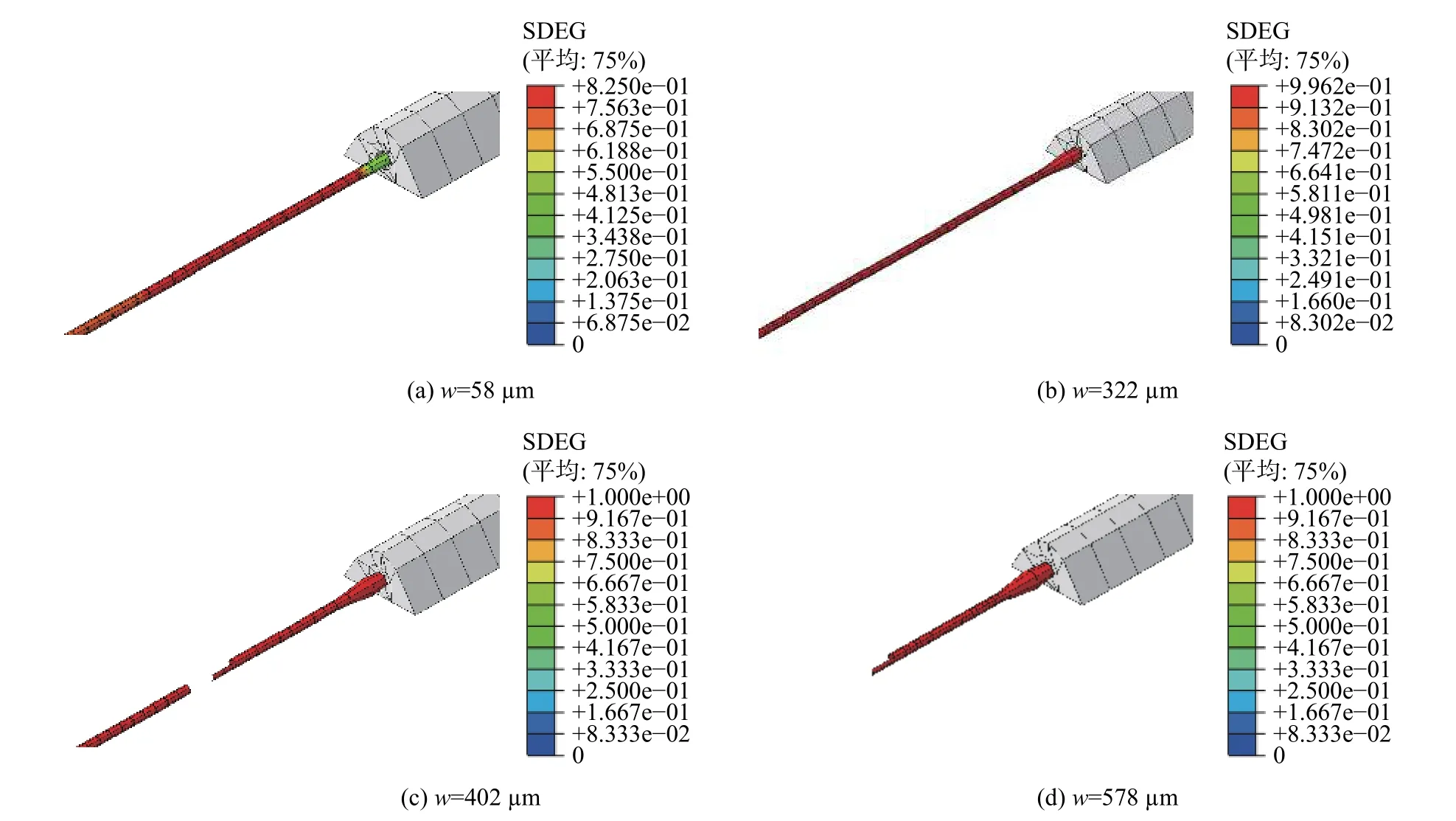
图10 不同裂缝宽度下Cohesive单元刚度退化云图

图11对有限元和实验结果的裂缝传递系数进行了比较，从图中可以看出，两者的吻合性较好。在裂缝宽度0.4 mm限值范围内，光纤伸长量与实际裂缝宽度呈正比例关系，拟合相关性达99%。FEM和实验结果均表明，较大强度的粘结层可以将裂缝等大变形更好地传递到光纤上，粘结层弹性模量为5.630 GPa的裂缝传递率高达98.3%，比粘结层弹性模量为0.473 GPa的光纤大2.5%。将光纤应变积分大小作为基体裂缝宽度的预测值，其误差范围小于5%。

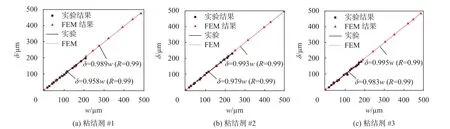
图11 有限元模型和实验结果光纤伸长量和裂缝宽度关系对比

4 结束语

本文提出了一种分布式光纤监测基体裂缝的数值分析方法，在理论分析基础上建立有限元模型，首次提出在光纤-涂覆层界面之间插入零厚度Cohesive单元模拟光纤监测裂缝扩展过程中出现的界面滑移，得到考虑界面损伤的光纤应变分布曲线。与传统光纤监测基体变形的数值模型相比，该模型能够更加真实地反映分布式光纤监测裂缝的变形传递过程。基于数值模型研究发现，在界面未出现滑脱之前，光纤应变峰值可以表示为裂缝宽度的幂函数，拟合相关性达99%，界面局部失效之后，光纤应变峰值则稳定在某一常数。分析表明光纤粘结层的弹性模量越大，基体向传感光纤的变形传递比越高，将光纤应变积分大小作为基体裂缝宽度的预测值，其误差范围小于5%。

通过分析分布式光纤监测裂缝扩展的应变传递机理，提出一种更加合理的数值分析方法，为分布式光纤在结构健康监测领域的应用提供了理论依据，从而为预测光纤监测大变形的应变分布以及合理优化光纤封装层参数提供一定参考，进而选择合理量程的光纤传感器设备。此外，本文得到的裂缝宽度传递系数可以用于光纤应变监测结果的换算，提高分布式光纤监测裂缝宽度的准确性。