光纤法测量冷弯中空玻璃板应力分布试验研究

徐自林， 张二毛， 张喜德,3， 江佳霖

(1. 广西大学土木建筑工程学院，广西 南宁 530004; 2. 南宁高速公路建设发展有限公司, 广西 南宁 530023; 3. 工程防灾与结构安全教育部重点实验室，广西 南宁 530004)

0 引 言

作为一种外围护结构，玻璃幕墙以曲面为美，由于冷弯成型法可以在常温下将玻璃弯曲成所需的形状，而且拥有成型效果好、成本低、能耗低和光学性能良好的优势[1]，因而有许多玻璃幕墙项目采用此方法进行施工。因为冷弯时玻璃发生的是弹性变形，因此其内部会存在永久应力[2]。由玻璃与硅酮胶、间隔条、丁基胶等间隔材料粘结而成的中空玻璃，间隔材料的剪切模量对其冷弯力学性能有重要影响[3]，并且在冷弯时其应力和变形状态相比于普通单片玻璃更加复杂，对此， Besserud[4]等研究了冷弯中空玻璃的耐久性，Pölzl[5]通过数值模拟的方法研究了中空玻璃在单曲率和双曲率冷弯下的力学性能，张喜德[6]等通过试验和有限元模拟研究了耦合均布荷载等因素对冷弯中空玻璃力学性能的影响。但是，现有的关于冷弯中空玻璃的研究较少，而且各试验研究中主要采取传统电阻应变法测量其应力，这极大地限制了冷弯中空玻璃的应用与发展。

由于光纤拥有抗干扰强、体积小、质量轻、耐腐蚀、可靠性好等特性[7]，因此其被广泛应用于土木工程领域，如Zhang等通过分布式布里渊光纤研究了路基的沉降行为[8]，提出了一种监测路基沉降的方法；冯其瑞等采用分布式光纤传感技术监测了高强筋活性粉末混凝土梁裂缝的发展[9]；张峰和裴华富研发了一种用于监测边坡位移的分布式光纤原位测斜仪[10]。虽然分布式光纤被广泛应用，但是在国内未发现有学者使用光纤研究冷弯玻璃的力学性能，在国外也鲜有发现，只有Thiemo Fildhuth等利用光纤传感器监测了冷弯夹层玻璃的内部应力[11]。

基于上述认识，本文对冷弯中空玻璃板的力学性能进行研究，利用分布式光纤的特点测量冷弯应力，以便在分析中空玻璃板在冷弯时沿光纤长度方向的应力分布规律及大小方面取得更好的实验效果。

1 分布式光纤的应力测量原理

在布里渊光时域分析（BOTDA）技术中，位于光纤两端的可调谐激光器分别将一泵浦光和探测光注入光纤，当泵浦光和探测光的频率差恰好等于光纤某区域的布里渊频移时，在该区域就会产生布里渊受激放大作用，两光束之间发生能量转移。由于布里渊频移与应变、温度存在良好的线性关系，因此在对两激光器的频率进行连续调节时，根据检测光纤一端耦合出来的连续光的功率，就可以确定光纤各小段范围内能量转移达到最大时所对应的频率差，从而得到应变和温度信息，实现分布式测量。当环境温度变化较小时，可以忽略温度对布里渊频移的影响，根据式(1)计算光纤的应变值。

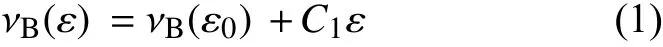
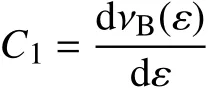
在试验中采用艾尔讯集团专门定制的裸光纤，其应变系数C1根据闫继送[12]等人的研究成果，取值为 0.051 1 MHz/µε。由于试验在室内进行，通过空调控制室温，使冷弯过程中室温保持在25℃±2℃范围内，环境温度变化较小，因此可按式(1)计算试验中光纤各测点的应变值。

根据分布式光纤采集到的应变数据以及玻璃的弹性模量可计算出冷弯中空玻璃板沿光纤长度方向的应力σ，玻璃的弹性模量值根据现行规范JGJ 102—2003《玻璃幕墙工程技术规范》取为72 000 MPa。

2 试验设计

2.1 试件设计

中空玻璃由玻璃板和间隔材料构成，如图1所示，为便于分析与描述，对图中玻璃板的四个大面进行命名，规则如下：“T”“D”分别表示上、下片玻璃，“1”“2”分别表示每片玻璃的上、下表面。例如，“D-1”面表示下片玻璃的上表面。

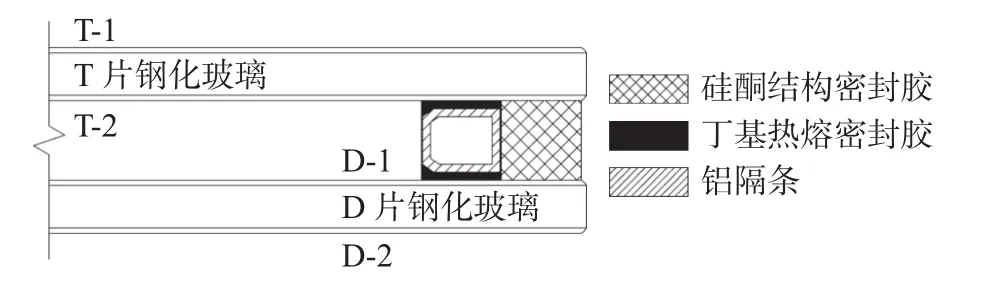
图1 中空玻璃的构造

根据中空玻璃的组成，研究玻璃厚度、空腔厚度和冷弯半径这3种因素对冷弯中空玻璃板长边边缘处应力分布的影响，每种因素取3个水平，按正交试验方法，共制作9个试件，试验方案见表1，表中t表示玻璃厚度，tc表示空腔厚度，r表示冷弯半径。参考实际工程中玻璃幕墙的规格，每一块中空玻璃的尺寸都采用 1 200 mm×600 mm；根据中空玻璃板的常用厚度，玻璃厚度t采用 4.6 mm、5.0 mm和 6.0 mm；空腔厚度tc按规范 JGJ 102—2003 采用9 mm、12 mm 和 15 mm；冷弯半径r采用 12 m、18 m 和 24 m。

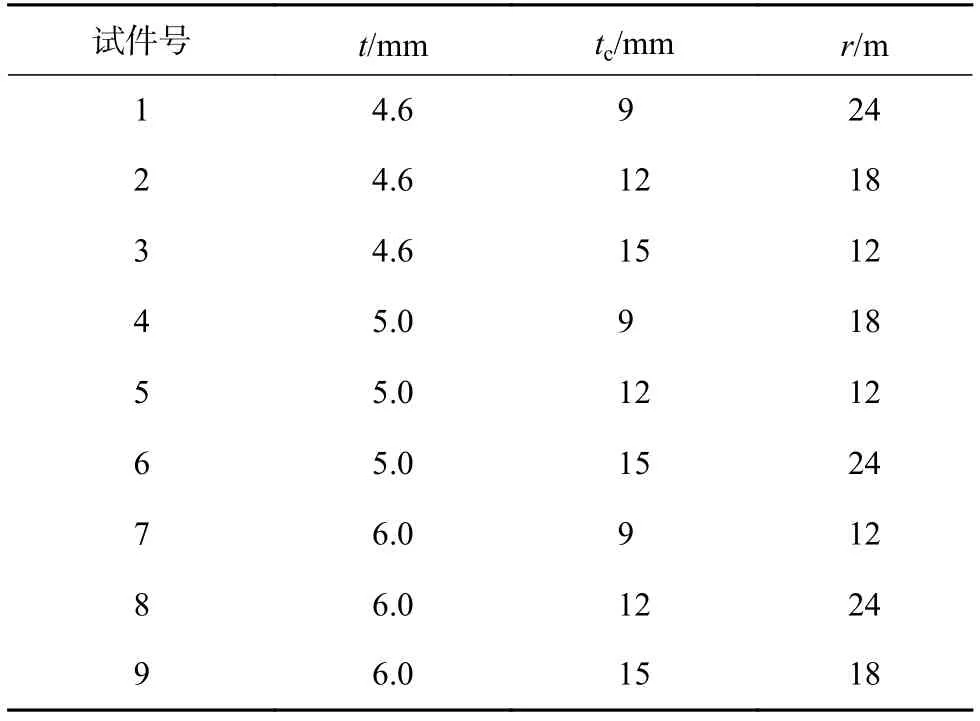
表1 试验方案

2.2 测点布置

为了研究冷弯后沿玻璃板长边边缘处的应力分布规律及大小，用分布式光纤对各冷弯中空玻璃板内面（T-2、D-1面）的应力进行采集。分布式光纤的布置如图2所示，由图中可知1号和2号光纤分别布置于T-2、D-1面。光纤的空间分辨率取为5 cm，按每5 cm取一个应力测点，并从固定端的A点往冷弯端的B点依次对测点进行编号，由于试件长1 200 mm，所以每根光纤共有24个应力测点。根据试件的边界条件及加载方式，试件关于X轴对称，故只在玻璃板的一条长边边缘布置光纤，同时在四个角点和长边中点布置有电阻应变片，如图2所示，用于验证试件的对称性以及与光纤所测的应力值作对比分析。此外，采用百分表对玻璃冷弯过程中的位移进行测量，在玻璃板的中部和两端各布置3个位移测点，通过位移的监测来控制冷弯位移的加载。

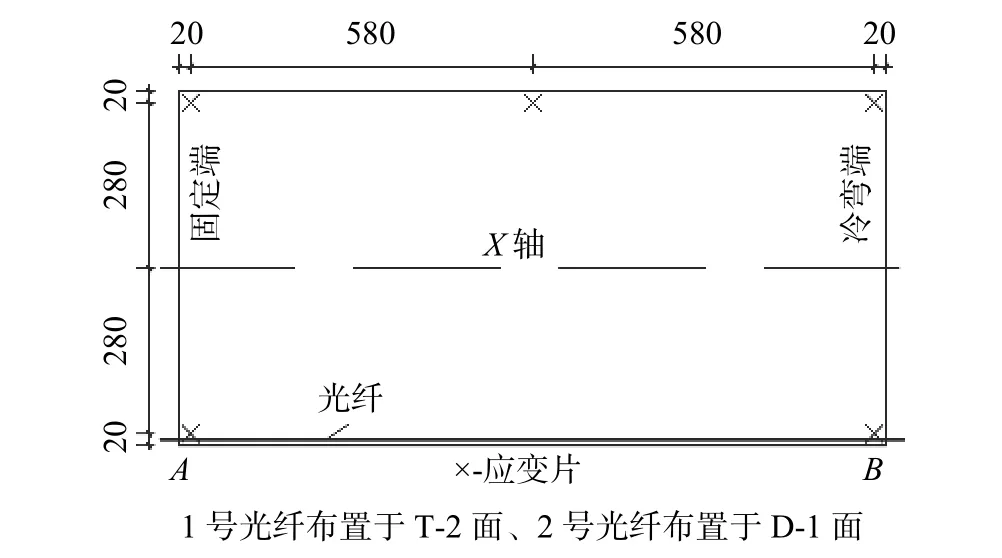
图2 光纤及应变片的布置（单位：mm）

2.3 试验方法

设计并制作一个专门的试验装置，用于模拟玻璃幕墙的支承结构和中空玻璃的冷弯位移加载，如图3所示。该装置主要由底座、钢横梁和曲边支承梁组成，其中，曲边支承梁采用印尼菠萝格木材进行制作，实物如图4所示。当玻璃被加载到与曲边支承梁贴合时即可得到相应的冷弯半径。

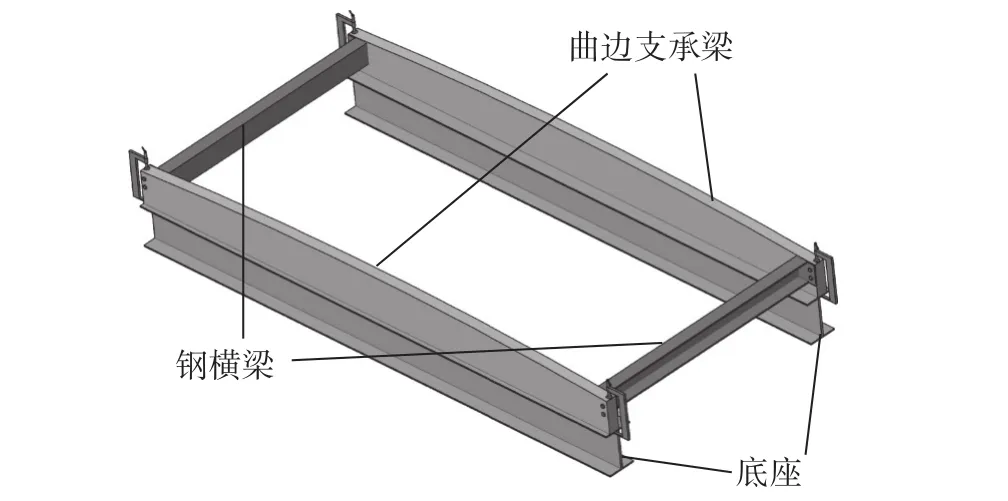
图3 冷弯试验装置

图4 曲边支承梁（单位：mm）

在加载前先用夹具将试件的一端固定在冷弯试验装置的钢横梁上，再放置铅块于试件的另一端，通过铅块的重力来实现玻璃板冷弯位移的加载。加载过程中采用分级加载的方式，每块铅块的质量为4.9 kg，每级荷载取2块铅块对称放置于玻璃板冷弯端，试件的冷弯状况如图5所示。试验过程中采用日本Neubrex公司生产的NBX-6050A光纳仪对布置在试件内面长边边缘的光纤进行数据采集，光纳仪如图6所示，该光纳仪在空间分辨率上可达到5 cm，应变测量的精度可达到±7.5 µε，采样间隔为5 cm，应变测量范围为-30 000～40 000 µε。由于中空玻璃板具有微小的滞弹性，所以在每级冷弯位移加载结束后，等待15 min再采集数据。

图5 冷弯状况

图6 NBX-6050A光纳仪

3 试验结果与分析

3.1 应力分布

将玻璃板四个角点处应变片所测沿长边方向的应力值进行对比，发现布置有光纤的两个角点与另外两个角点的应力偏差在8.33%之内，表明在冷弯试验过程中中空玻璃板关于X轴具有良好的对称性。根据分布式光纤采集到的数据可绘制冷弯中空玻璃板沿光纤长度方向的应力分布图，如图7所示，图中应力以拉为正，以压为负。

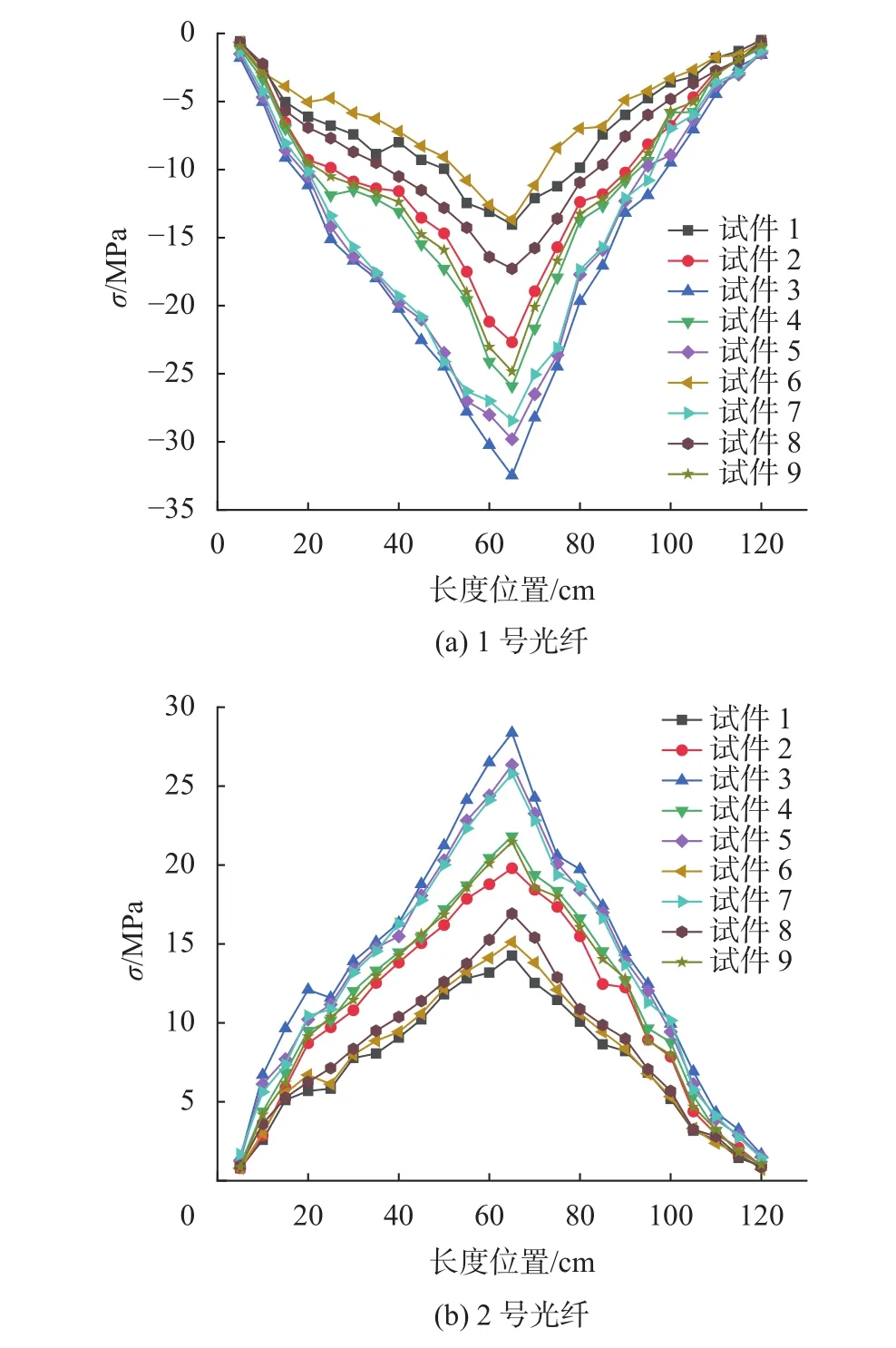
图7 玻璃板上光纤所测的应力分布图

由图中可知，分布式光纤在测量冷弯中空玻璃板的应力分布时出现了小幅波动，这主要是受到仪器测试误差的影响，总体上看，实验数据较为完善，测量效果也比较好，说明分布式光纤可以较准确地测量冷弯中空玻璃板的应力分布；最大应力值出现在长边中点，并由中部向两端逐渐减小，试件在弯曲状态下的应力表现出上拉下压、中间大两边小的分布规律。

根据冷弯试验结果，最大试验应力值如表2所示，从表中可以看出最大应力值出现在冷弯半径最小的试件3，而且冷弯半径不同，应力值相差很大，表明冷弯半径对应力的影响很显著。

表2 最大应力值

3.2 极差分析

按正交法设计的试验结果需进行极差分析来确定各影响因素的重要程度。由于最大应力值出现在T-2面的1号光纤，所以只分析各因素对T-2面长边边缘处最大应力的影响。极差R分析的结果见表3，表中（j=1,2,3）表示各因素在水平j上的平均值，由表中可知，冷弯半径对应的极差为15.24，空腔厚度与玻璃厚度的极差分别为0.86和0.46，后两种因素的极差比冷弯半径的小很多，因此，在所研究的因素中，冷弯半径对冷弯应力的影响最大。

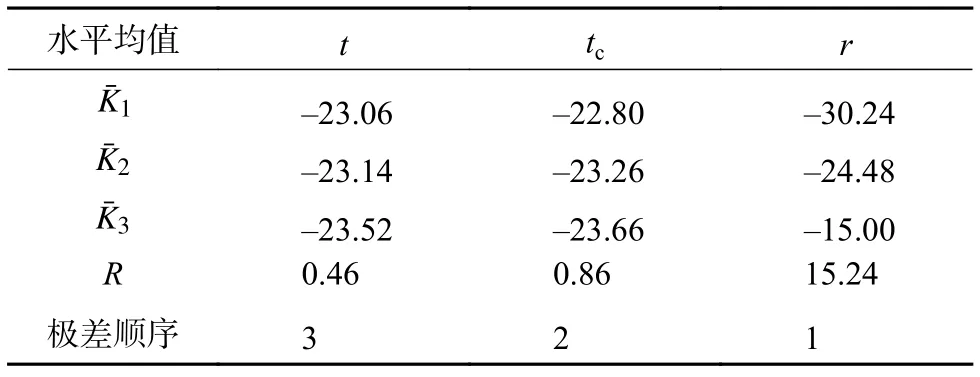
表3 T-2面各因素的最大应力极差

3.3 冷弯半径的影响

根据正交试验结果，不同冷弯半径下冷弯中空玻璃板长边最大应力值变化情况见表4，由表中可知，当冷弯半径从 12 m 增加到 24 m 时，T-2、D-1面应力分别减小50.40%、42.49%，说明随着冷弯半径增加，最大应力会有明显的下降。

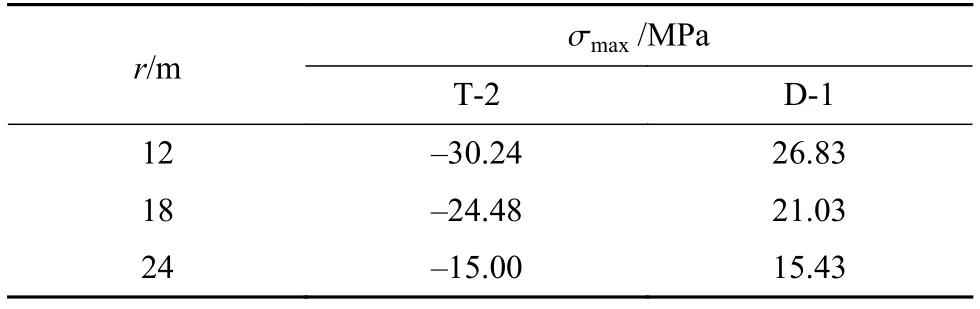
表4 冷弯半径对最大应力的影响

3.4 空腔厚度的影响

试验结果中空腔厚度的变化与冷弯中空玻璃板长边最大应力值的关系见表5，由表中可知，随着空腔厚度的增加，最大应力值也增加，当空腔厚度从9 mm 增加到 15 mm 时，T-2、D-1 面应力分别增加3.77%、5.00%。与冷弯半径影响相比，空腔厚度对最大应力影响较小，这主要是由于中空玻璃的刚度虽然随着空腔厚度增大而有所增加，但是形成空腔的间隔材料是一种粘弹性材料，其剪切刚度较小，对玻璃板的应力影响很小，因此其应力增幅较小。

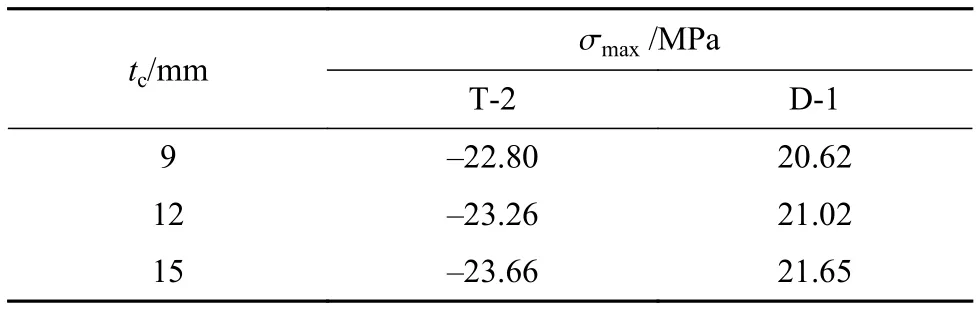
表5 空腔厚度对最大应力的影响

3.5 玻璃厚度的影响

玻璃厚度的变化对冷弯中空玻璃板长边最大应力值的影响见表6，由表中可知，随着玻璃厚度的增加，最大应力值也增加，当玻璃厚度从4.6 mm增加到 6.0 mm时，T-2、D-1面最大应力值分别增加1.99%、2.79%，说明玻璃厚度对最大应力的影响很小。由于玻璃厚度增加，中空玻璃板的刚度也会随着增加，但玻璃厚度的变化较小，因此玻璃板的应力增幅也很小。

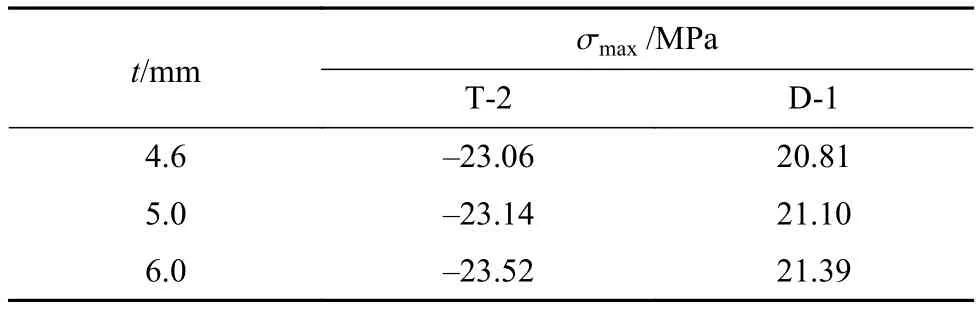
表6 玻璃厚度对最大应力的影响

3.6 光纤与电阻应变片的应力对比分析

根据最大应力所在位置，将位于长边中点的应变片（与光纤关于X轴对称）与光纤相应测点所测的应力值进行对比分析，对比结果见表7，其中应变片所测的应力值对比的是光纤测点12与测点13之间的应力均值。由表中可知光纤与应变片所测应力的相对误差在8.86%之内，经计算可得两种测量方法的相对误差平均值为4.74%，误差较小，而且分布式光纤所测的应力均比应变片所测的大，出现这种现象主要是因为分布式光纤离玻璃板的边缘更近，边缘的应力更大，故光纤所测的应力值更大。以上说明分布式光纤的测量精度可以较好地满足试验要求，因此，采用分布式光纤测量冷弯中空玻璃板的应力分布是可行的。

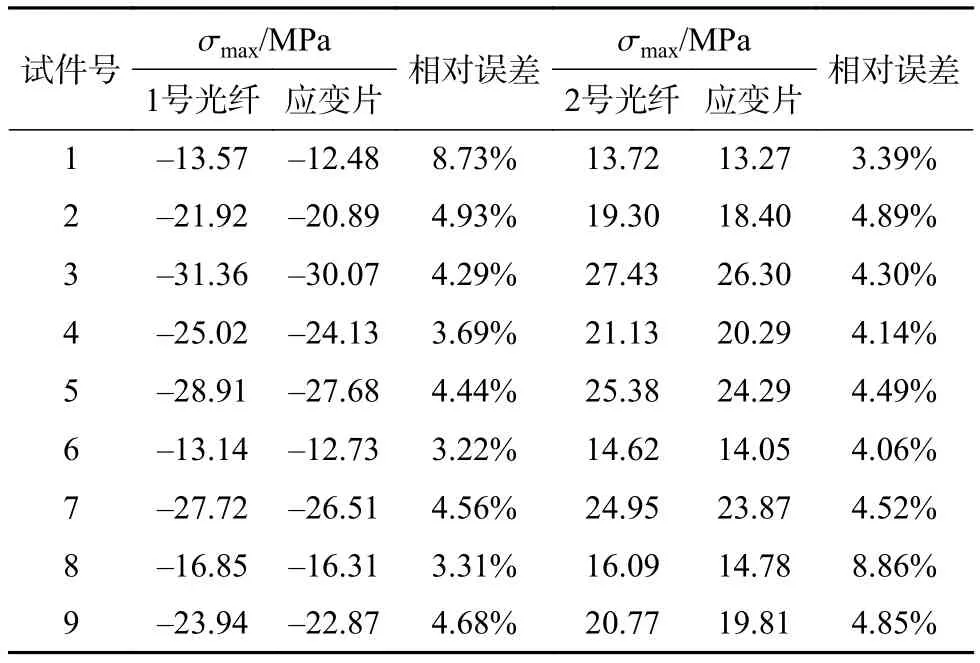
表7 光纤与应变片的最大应力值对比

结合分布式光纤的特点及试验结果，可以发现在测量冷弯应力时，分布式光纤测量法比传统电阻应变法更为方便与实用，同时可以较好地分析中空玻璃板在冷弯时沿光纤长度方向的应力分布规律，并取得更完善的实验数据。

4 结束语

1）分布式光纤测量中空玻璃板的冷弯应力分布时有微小的波动，但是总体上能够比较准确地反映冷弯应力的分布情况。

2）冷弯半径对冷弯应力的影响远大于空腔厚度和玻璃厚度，后两者的变化较小，对冷弯应力的影响很小。

3）分布式光纤与电阻应变片在应力测量上的相对误差平均值为4.74%，光纤的应力测量精度能较好地满足试验要求。

4）利用分布式光纤的特点测量冷弯应力比传统电阻应变方法更为方便与实用，可以较好地分析中空玻璃板在冷弯时沿光纤长度方向的应力分布规律，能取得更完善的实验数据。