基于变量重要度指数和FT-IR光谱的食用油分类研究

申 琦，李 盎，张晓芋，桑泽农，王志莹

(郑州大学 化学学院 河南 郑州 450001)

0 引言

食用油是人们日常生活中重要的食品之一，包含有大豆油、玉米油、花生油、葵花籽油以及橄榄油等。由于不同食用油的功效、营养价值和价格有很大差异，不法商贩会将廉价油掺入优质油中以次充好。传统的食用油品质分析是通过检测色泽、比重、折光率、皂化值、酸值、羰基值、过氧化值、电导率等理化指标，进行品质鉴定与分类，具有消耗试剂多、操作复杂耗时等缺点[1-2]。随着人们食品安全意识的逐渐提高，发展低成本、快速可靠和无损的食用油筛选检测技术是很有必要的[3-5]。

傅里叶变换红外光谱(FT-IR)技术是一种无损、绿色且高效的分析技术[6]，具有样品预处理简单、分析速度快等优点，广泛应用于基础和应用化学研究中。但是，由于FT-IR光谱变量较多，光谱重叠严重且难以解析，经常需要结合变量筛选和多元校正方法对光谱数据进行分析[7-8]。常用的变量筛选方法有无信息变量消除算法、连续投影算法、竞争自适应加权采样算法[9]、遗传算法[10]和粒子群优化算法[11-12]等。其中，粒子群优化算法具有概念简明、收敛速度快以及需要调整的参数较少等优点，但其在用于变量筛选时仍会在一定程度上陷入局部最优，结果不够理想。本文采用离散粒子群优化算法对五种食用油进行分类，为进一步优化算法性能，将变量重要度指数引入离散粒子群优化算法的初始化过程中，并利用轮盘赌算法增大重要度大的变量的筛选概率，获得了较好的分类效果。

1 实验部分

1.1 实验样本

全部77个食用油样本均从当地超市中购买，包括21个玉米油、24个橄榄油、14个花生油、11个葵花籽油和7个大豆油。采用随机分类方法将77个样本分为含有51个样本的训练集和含有26个样本的预测集。其中，训练集含有14个玉米油、16个橄榄油、9个花生油、7个葵花籽油和5个大豆油，剩余样本为预测集。这些食用油样本的傅里叶变换红外光谱(FT-IR)的波数范围为650～4 000 cm-1,分辨率为2 cm-1，将光谱数据变换到(0，1)进行定性分析。

1.2 实验方法

1.2.1改进的离散粒子群优化算法 粒子群优化算法(particle swarm optimization,PSO)是Kennedy和Eberhart[13]通过对鸟群觅食行为的研究，提出的一种启发式的全局优化方法。PSO算法首先随机生成N个初始粒子，每个粒子都有一个位置和速度，算法会记住所有粒子在搜索过程中找到的全局最佳位置和每个粒子所找到的个体最佳位置。粒子通过跟踪两个最佳位置更新自己，迭代找到最优解。

离散粒子群优化算法初始化是随机产生个体，虽然随机初始化群体可以保证个体分布的均匀性，但是初始化的个体粒子可能距离最优解较远，从而增加了方法的收敛难度以及计算量。本文在初始化过程引入变量的重要度指数，可以缩短搜索路径，提高算法的收敛速度。

某个变量在不同样本中的差异越大，则其可能包含的信息量就越大。衡量变量在不同样本中的差异性可以用变量的光谱纯度(Pi)[14]表示，光谱纯度定义为每个变量的光谱标准偏差(σi)与光谱均值(μi)的比值，即

Pi=σi/μi。

(1)

变量的光谱纯度值越大，意味着不同样本在该波长变量处的吸光度数值有较大的差异，该变量可能为强信息变量。在多种变量筛选方法中，变量的偏最小二乘(partial least squares,PLS)回归系数的绝对值是一种常用的衡量变量重要性的指标，回归系数绝对值大的变量说明其对模型的贡献量大。

分别归一化变量的PLS回归系数(bi)和光谱纯度(Pi) ，将二者的乘积作为变量的重要度指数(VIi)，即

VIi=Pi*bi。

(2)

基于变量重要度指数的离散粒子群算法将变量重要度用于初始化选择变量，其具体步骤如下。

Step 1 首先计算每个变量的重要度指数，并按降序排列。为保证算法的随机性，没有直接选择重要度最高的变量构成粒子，而是引入轮盘赌算法为每个个体选取一定数量的变量。采用轮盘赌算法，则重要度大的变量选中的概率较大，重要度小的变量选中的概率较小。一般而言，选中的变量的概率由问题决定。本研究中每个个体选取8%的变量，对选取的变量进行二进制编码(0/1)，即被选中的8%的变量为1，其余的变量为0。

Step 2 根据目标函数计算每个粒子的适应度值。粒子当前最优位置为Pbest，粒子群体中最佳粒子位置为Gbest。

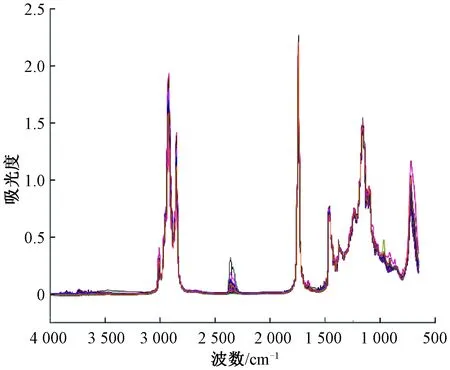
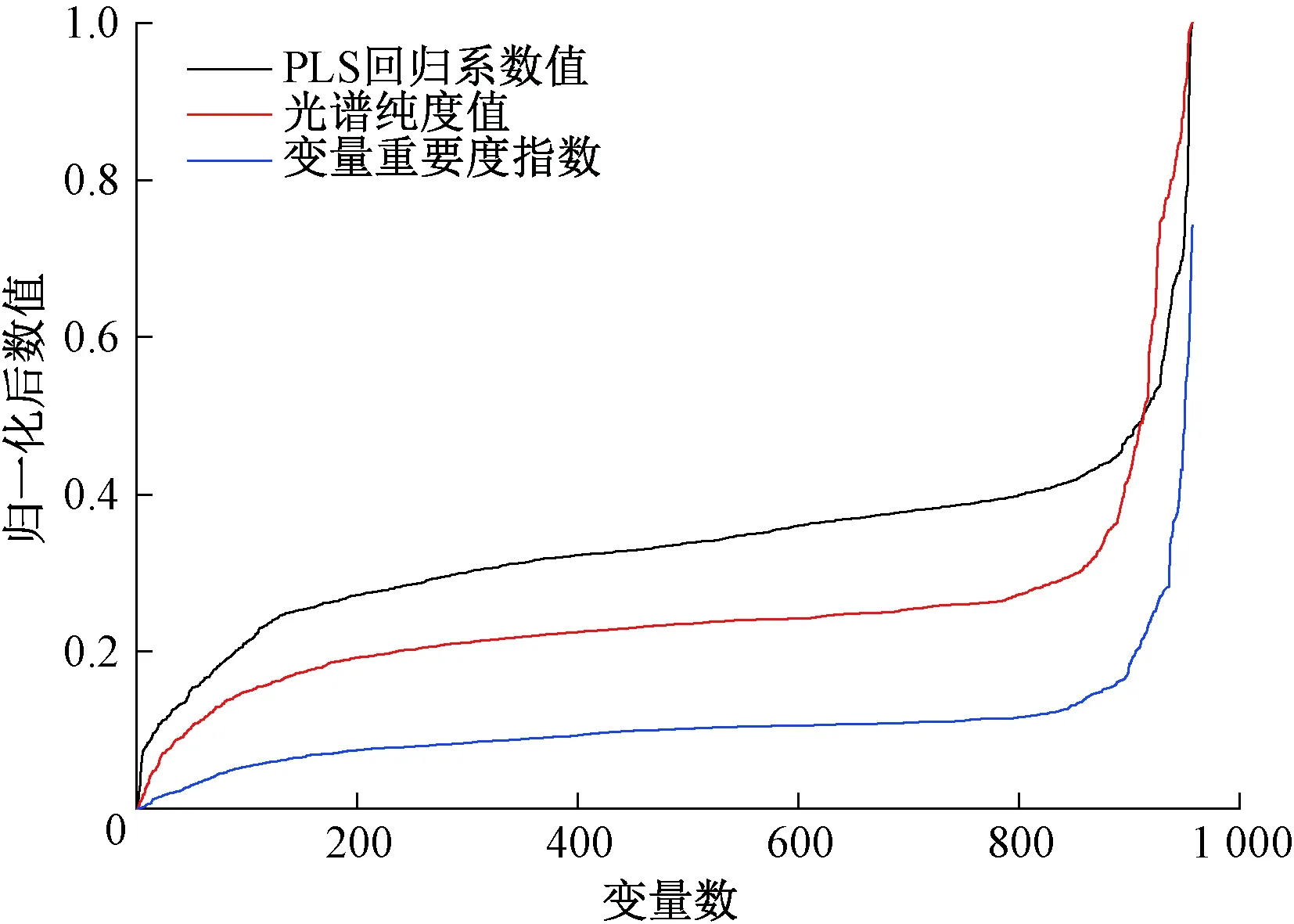
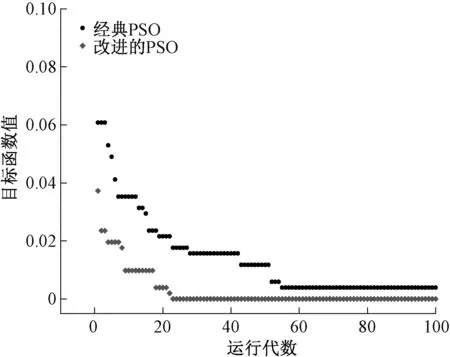
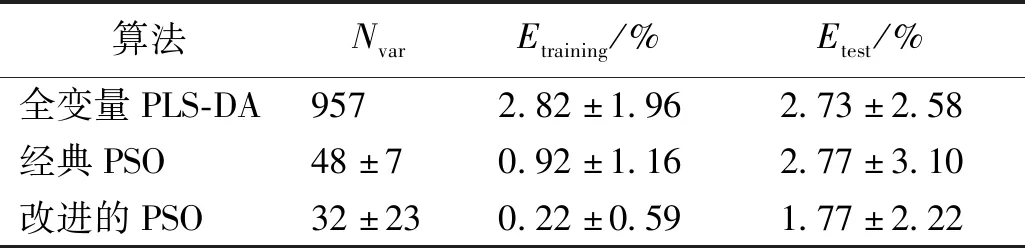
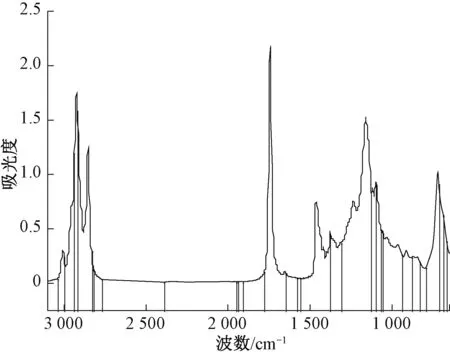
Step 3 对粒子的位置以及速度进行更新。当0

Step 4 如果满足终止条件，则输出解。否则，返回Step 2。

1.2.2目标函数 目标函数采用了基于自助抽样的Bootstrap交叉验证方法。Bootstrap方法[15]是采用重抽样技术从原始数据中随机选取m个样本，建立分类模型，并预测其他未选中的样本，该过程重复N次，取N次分类错误率的平均值。本文采用3倍交叉验证，采样次数为10，将交叉验证分类错误率的平均值作为该粒子的目标函数值。

2 结果与讨论

实验数据集含有玉米油、橄榄油、花生油、葵花籽油和大豆油共77个食用油样本，在650～4 000 cm-1波数范围内，间隔2 cm-1扫描红外吸收光谱，每个样本获得957个光谱变量。图1为77个食用油样本的FT-IR光谱。

图1 食用油样本的FT-IR光谱Figure 1 FT-IR spectra of edible oil samples

由图1可以看出，不同样本的FT-IR光谱分布基本相同，重叠情况非常严重。在这些FT-IR光谱中，样本的特征峰数、峰形和峰的位置都是相似的,表明不同种类食用油的主要成分大致相同。

本文基于全部957个变量建立偏最小二乘判别分析(PLS-DA)分类模型。采用训练集的51个样本构建PLS-DA模型，再用此模型对26个预测集的样本进行预测。采用全变量模型获得的训练集和预测集的分类错误率分别为1.96%和3.85%。

由于采用了全部变量，变量中可能含有无信息变量以及噪音，而这些无关变量参与建模会降低模型的预测能力。为了降低模型的分类错误率，应用PSO算法优化筛选变量的PLS-DA方法。首先采用了经典PSO算法，即初始化步骤为随机挑选变量。随机初始化大约5%的变量，运行100代，采用最优个体筛选得到的变量建立PLS-DA分类模型。PSO算法优化筛选到48个变量，模型的训练集和预测集的分类错误率分别为0和3.85%。虽然PSO算法准确地分类了全部训练集的食用油样本，但是预测集的分类错误率并未降低，表明PSO算法优化筛选变量的PLS-DA方法获得的模型可能存在过拟合现象，暗示着PSO算法筛选获得的变量中可能仍存在无信息变量。

使用改进的离散PSO算法，在初始化步骤引入变量重要度指数和轮盘赌算法。图2显示了不同变量的重要度指数、PLS回归系数值和光谱纯度值经过归一化计算后排序的分布情况。可以看出，大部分变量的重要度数值不大，仅有大约十分之一的变量具有较大的重要度数值。

图2 变量重要度指数、PLS回归系数值和光谱纯度值的分布Figure 2 The distribution of the variable importance index,regression coefficient of PLS and spectral purity value

对全部变量进行筛选，最后选择了32个变量，训练集和预测集的分类错误率均为0。改进前后PSO算法的目标函数收敛情况如图3所示。可以看出，经典PSO算法需要54代收敛，而改进的PSO算法经过23代运算就能达到收敛，收敛速度更快，而且改进的PSO算法获得的目标函数值更小，结果更准确。

图3 改进前后PSO算法的目标函数收敛曲线Figure 3 Objective function convergence curve of PSO algorithm before and after improvement

由于训练集和预测集的分类为随机分类，为获得更准确的结果，对样本集随机进行了100次分配，将不同训练集和预测集获得的分类结果进行平均，并计算100次结果的标准偏差。全变量PLS-DA方法、经典PSO算法和改进的离散PSO算法的平均结果见表1。

表1 不同方法100次分配训练集和预测集的平均结果Table 1 Average results of 100 assignments of training sets and prediction sets by different methods

由表1可以看出，全部957个变量的PLS-DA模型的训练集和预测集的平均分类错误率分别为2.82%和2.73%，100次运行结果的标准偏差为1.96%和2.58%。经典PSO算法得到大约48个变量，训练集和预测集的平均分类错误率分别为0.92%和2.77%，标准偏差分别为1.16%以及3.10%。与全变量PLS-DA方法的结果进行对比，采用PSO算法筛选变量后训练集的平均分类错误率有了明显的降低，并且标准偏差也较小；预测集的分类错误率略有升高，且波动较大。改进的离散PSO算法得到大约32个变量，训练集和预测集的平均分类错误率分别为0.22%和1.77%，标准偏差分别为0.59%和2.22%。通过对比可以看出，改进的PSO算法筛选得到较少的变量，训练集和预测集的结果均有明显的改善，且标准偏差较小，表明结果具有一定的稳定性。引入变量重要度指数来衡量变量的重要性，不仅可以优化PSO算法的收敛速度，还减少了计算量，且收敛值更优。

图4 改进的PSO算法筛选得到的变量分布Figure 4 The variable distribution selected by the modified PSO algorithm

综上，使用FT-IR光谱技术结合化学计量学建立模型对五种食用油进行分类，具有无损、试剂消耗少等优点，可以未经预处理进行直接和快速的测定。此外，改进的PSO算法的分类错误率相比经典PSO算法和全变量PLS-DA分类模型有明显降低，可实现对食用油样品快速、准确的分类。

3 小结

本文提出了基于变量重要度指数的离散PSO算法，将PLS回归系数和光谱纯度的乘积作为变量的重要度指数，引入离散PSO算法的初始化过程中，并利用轮盘赌算法增加算法的多样性。实验结果表明，改进的离散PSO算法收敛速度快，计算量较少。与经典PSO和全变量PLS-DA方法相比，改进的离散PSO算法可以跳出局部最优，找到最优解，是一种快速、无损的食用油分类方法。