一种高光谱图像加权稀疏子空间聚类算法

樊 娟，邓秀勤，火博丰，王卓薇

(1.广东工业大学 数学与统计学院 广东 广州 510520；2.青海师范大学 数学与统计学院 青海 西宁 810008；3.藏语智能信息处理及应用国家重点实验室 青海 西宁 810008；4.广东工业大学 计算机学院 广东 广州 510006)

0 引言

随着光谱成像技术的发展，高光谱图像(hyperspectral images,HSIs)已经成为检测技术的一个有效工具。HSIs广泛应用于目标检测[1-2]、精准农业[3]、环境监测[4]和公共安全[5]等领域。随着HSIs技术的发展，HSIs分析处理也变得越来越重要。近年来，高光谱图像聚类作为高光谱图像分析处理的手段之一，备受关注。

HSIs是典型的高维数据，具有十分复杂的内部结构、多变的地物光谱信息。一些传统的方法已被用于HSIs聚类，如K均值聚类[6]和模糊C均值聚类[7]，这类方法对初始化和噪声相对敏感。由于光谱域中的判别信息有限，地面物体的复杂性以及同一类别中光谱特征的多样性，直接在HSIs上应用这些方法往往会产生带有大量噪声的聚类图。基于图谱的方法谱聚类(SC)[8-10]，由于HSIs内部结构的复杂性，以及谱聚类对光谱变化的有限适应性，直接将谱聚类应用于HSIs得到的聚类结果是不理想的。近年来，子空间聚类方法在高光谱遥感领域得到了广泛关注，并取得了显著的成绩。子空间聚类算法实际上是将传统的特征选择技术和聚类算法进行结合，在对数据样本聚类划分的过程中，得到各个数据簇对应的特征子集或特征权重。自Elhamifar等[10]提出稀疏子空间算法后，出现了众多的衍生模型。主要包括稀疏子空间聚类算法[11](sparse subspace clustering,SSC)和低秩子空间聚类算法[12](low rank representation，LRSC)。这些算法的关键是找到原始数据的稀疏或低秩表示矩阵，然后在相应的稀疏系数矩阵上建立相似图，并利用谱聚类得到聚类结果。

SSC算法已经应用于人脸聚类[13]、运动分割[14]和计算机视觉[15]等，但SSC算法也存在一些局限性，一方面SSC依赖于稀疏自表示模型来重建亲和力矩阵，这导致SSC算法对HSIs聚类的潜力没有被全部开发出来；另一方面SSC独立处理每个像素，对HSIs的光谱相关性和空间相关性利用不够充分。在HSIs的稀疏子空间聚类中，为利用HSIs丰富的光谱信息和空间信息，文献[16]利用欧几里得距离度量稀疏相似矩阵，提出了余弦-欧氏动态加权相似矩阵(CEDW)的构造方法，但该方法在重构亲和力矩阵时易受到异常像素的干扰。文献[17]考虑到HSIs的光谱相关性和丰富的空间信息，提出了一种谱空间稀疏子空间聚类方法(S4C)来提高聚类性能，但该方法需要通过子空间检测自动确定集群数量和自适应确定正则化参数。本文提出了一种基于弗雷歇距离的高光谱图像稀疏子空间聚类算法(sparse subspace clustering algorithim based on Fréchet distance,FSSC)。该方法一方面利用SSC算法求解全稀疏表示矩阵，探索HSIs在低维子空间的结构；另一方面考虑像素点间的光谱信号的相关性，以及传统的子空间模型容易受到欧几里得域中的噪声数据和异常值的影响，利用弗雷歇距离度量相似度，建立光谱加权稀疏子空间聚类模型，基于稀疏系数矩阵和相似度矩阵重构亲和力矩阵，以确保每个像素的稀疏表示更接近真实的情况，最后将亲和力矩阵应用于谱聚类，得到聚类结果。

本文的贡献如下。

1) 将同一土地覆盖类的像素视为位于一个独立的子空间，利用稀疏子空间模型求解稀疏自表示矩阵。

2) 考虑HSIs丰富的光谱信息和像素点间的光谱相关性，利用弗雷歇距离度量像素点光谱曲线间的相似度。

3) 建立FSSC模型，利用稀疏自表示和光谱连续性学习更有利的表示矩阵，充分挖掘了HSIs的光谱结构信息。通过加权稀疏约束，更好地探索了HSls的结构信息。

1 相关工作

1.1 HSls的稀疏子空间聚类算法

稀疏子空间聚类是一种基于谱聚类的子空间聚类框架，基本思想是假设高维数据能够在低维子空间中进行线性表示，然后根据表示系数矩阵构造亲和力矩阵，最后将亲和力矩阵应用于谱聚类。稀疏子空间聚类的优化问题模型为

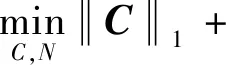
s.t.Y=YC+N，diag(C)=0，CT1=1，

(1)

其中：Y是高维数据矩阵；C是稀疏系数矩阵；N表示误差矩阵；λ是系数矩阵稀疏性和数据保真度的平衡参数。约束diag(C)=0用来消除表示像素点自身的琐碎解，diag(C)表示矩阵C的对角元素。另外，约束CT1=1确保了向量元素具有合适的大小，其中1表示一个全1列向量。这个目标函数是一个可处理的凸优化问题，可以用交替乘子法(ADMM)[18]来求解。然后构造亲和力矩阵，

W=(|C|+|C|T)/2，

(2)

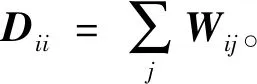
针对HSIs的稀疏子空间聚类，假设三维高光谱图像大小是M×N×B，M、N分别表示图像的高度和宽度，B表示光谱的数目，通常情况下先将高光谱图像数据展开为二维矩阵Y=[Y1，Y2，…，YMN]∈RB×MN，利用SSC模型的公式(1)可以求解HSls稀疏系数矩阵C，再利用公式(2)求解亲和力矩阵W，最后将谱聚类应用于亲和力矩阵，得到聚类结果。

1.2 基于弗雷歇距离的相似度矩阵

1.2.1弗雷歇距离 弗雷歇距离算法在相似性识别方面具有优势，并已成功地应用于签名手写识别、计算机图形以及地理等领域[21-22]。弗雷歇距离的定义为[23]，设A和B是S上的两条连续曲线，即A:[0,1]→S,B:[0,1]→S。又设α和β是单位区间的两个重参数化函数，即α:[0,1]→S,β:[0,1]→S。则曲线A和B的弗雷歇距离定义为

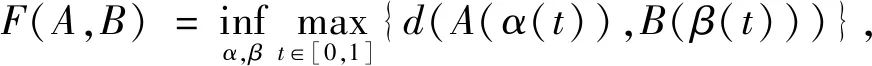
(3)

其中：d是S上的度量函数。

1.2.2基于弗雷歇距离的相似度矩阵Yi、Yj是像素点i和j的光谱值向量，这里定义两个非连续的映射为f:[0,1]→Yi，g:[0,1]→Yj，曲线yi、yj表示Yi、Yj对应的光谱值曲线，引入离散的弗雷歇距离

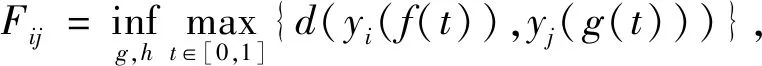
(4)

其中：d是R上的度量函数。在这里选择欧拉距离作为度量，即两点间在几何空间上的最小距离。连续的光谱值曲线间的弗雷歇距离首先要找出这无穷多个距离中的最大值，即在yi、yj上两个采样点yi(f(t))与yj(g(t))之间的欧氏距离最大值。然后找到这一系列采样点距离最大值的下确界，即该最大距离最小化的采样方式下的值。这个值就是弗雷歇距离。

对于HSIs而言，考虑到高光谱图像像素光谱带的连续性，本文将像素点的光谱值向量映射为光谱曲线。为了保证所有的权重都在0～1范围内，对弗雷歇距离矩阵F进行归一化处理，求解对应光谱曲线，

(5)

其中：Fi.表示弗雷歇距离矩阵F第i行的和。

2 HSls聚类的FSSC算法

本文提出了一种用于HSIs聚类的相似矩阵构造方法(FSSC)。该方法构造的相似矩阵结合了整体稀疏表示矩阵和HSIs的光谱信息。首先，该算法通过稀疏表示模型探索高光谱图像的稀疏表示矩阵。然后，为充分利用HSIs的光谱信息并克服SSC算法对异常值的敏感性，引入弗雷歇距离度量像素点间的相似度。最后，为确保HSIs中高度相关的像素参与表示过程，在亲和力矩阵重构的过程中添加一个光谱约束来获得一个更精确的亲和力矩阵。FSSC算法的主要流程如图1所示。

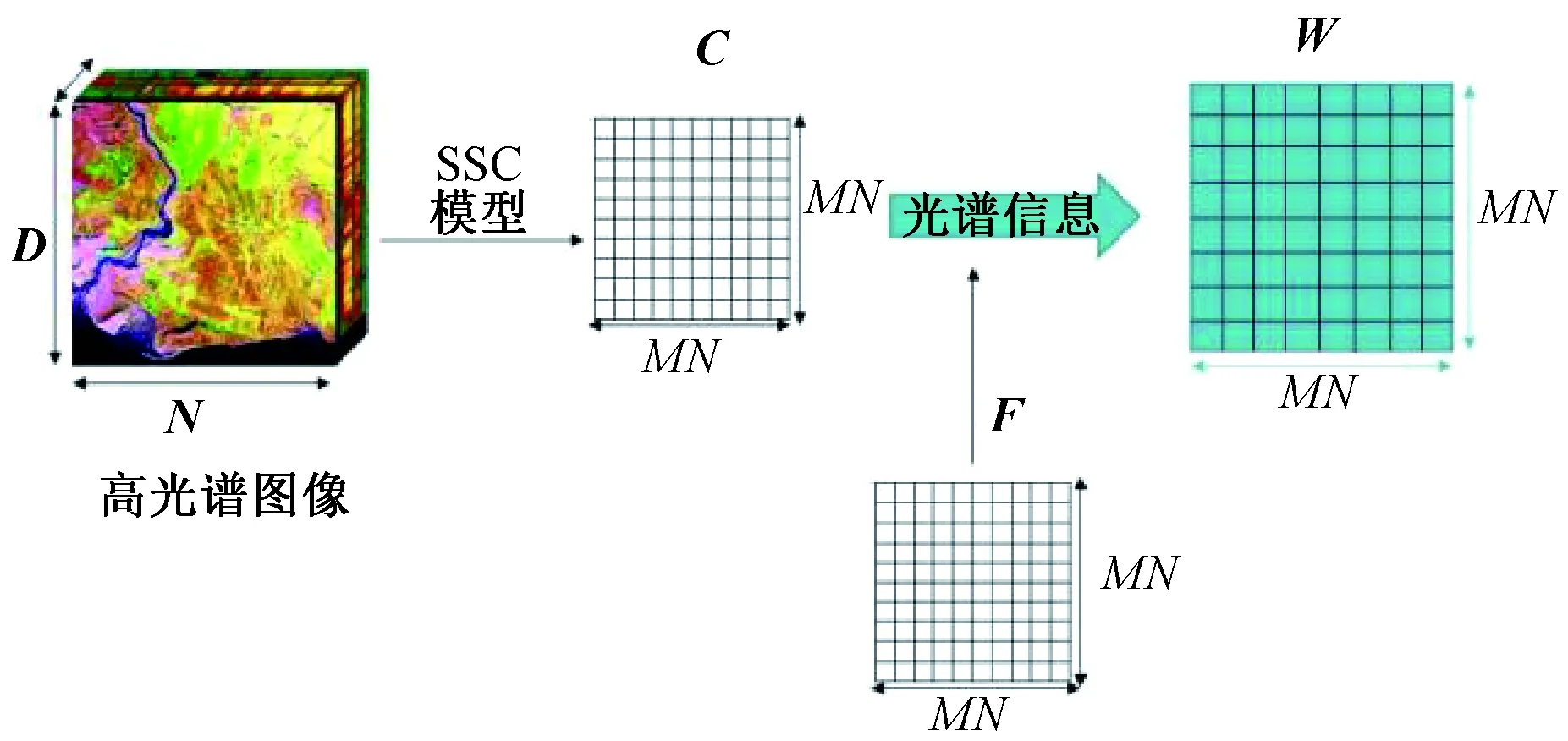
图1 基于弗雷歇距离的稀疏子空间聚类相似矩阵构造方法Figure 1 Construction of sparse subspace clustering similarity matrix based on Fréchet distance

由于相似数据点具有高概率共享同一子空间的特点，通过对相似数据点施加更大权重、对不同数据点施加更小权重来建立FSSC模型。对于HSIs来说,添加光谱信息和光谱相关性来改进SSC中亲和力矩阵的构造，可以很大程度上提高HSIs的聚类精度。因此，通过加权稀疏优化问题，可以实现更精确的HSIs表示系数矩阵C，

s.t.diag(C)=0,CT1=1,

(6)

其中：F作为一个光谱信息添加到稀疏表示矩阵中。与式(1)不同的是，这里通过弗雷歇距离矩阵的加权，可以有效利用像素点间的相似性来调节相似图边的权重，并求解更真实的亲和力矩阵，该问题可以通过ADMM算法求解。引入辅助变量A，将优化问题转化为

s.t.diag(C)=0,AT1=1,A=C。

(7)

式(7)的增广拉格朗日函数为

(8)

固定A，对C求导数并令其等于0，

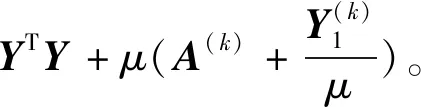
(9)

同理，

(10)

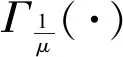
(11)

(12)

当‖A(k)T-C(k)‖∞≤ε,‖A(k)-C(k)‖∞≤ε或者‖A(k+1)-A(k)‖∞≤ε时，迭代将被终止，ε表示原始和双残差的误差公差。受基于质心簇方法的启发，较短弗雷歇距离内的高光谱像素在特征空间中具有较高的相关性[24]。因此，可以选择弗雷歇距离矩阵F作为光谱加权约束矩阵。面向高光谱图像的FSSC算法可归纳为算法1。

算法1高光谱图像的FSSC算法

输入：HSIs图像Y=[Y1，Y2，…，YMN]∈RB×MN，簇数k，正则化参数λ。

输出：聚类结果C1,C2,…,Ck。

1) 通过式(4)求解弗雷歇距离矩阵，并根据式(5)归一化处理；

2) 由式(6)构造FSSC优化模型，求解稀疏系数矩阵C；

3) 利用相似度矩阵F对系数稀疏表示矩阵C进行加权重构;

4) 根据式(2)求解亲和力矩阵W；

5) 将亲和力矩阵W应用于谱聚类。

3 实验结果分析

3.1 实验数据集

Indian pines数据集是由AVIRIS传感器获得的。本文考虑计算效率，选择了大小为85×70的子图像来验证算法的有效性，其中包括4个主要的土地覆盖类型：Corn_no_till、Grass、Soybeans_no_till、Soybeans_minimum_till。肯尼迪航天中心(kennedy space center,KSC)数据集由AVIRIS传感器获取的，大小是512×614，包含了13个土地覆盖类型，分别是Scrub、Willow swamp、CP hammock、Slash pine、Oak、Hardwood、Swamp、Graminoid marsh、Spartina marsh、Cattail marsh、Salt marsh、Mud flats、Water。

3.2 评价标准和对比算法

在这一部分中，为评估FSSC算法的有效性，分别将K均值(K-means)、模糊C均值(FCM)、谱聚类(SC)、稀疏子空间聚类(SSC)、欧氏余弦动态权重法(CEDW)和光谱空间稀疏子空间聚类(S4C)算法作为对比算法。本文选择用户精度(user′s accuracy，UA)、总体精度(overall accuracy,OA)和Kappa系数(Kappa)来评估FSSC算法的聚类性能。

3.3 实验结果和分析

3.3.1Indian pines数据集聚类结果分析 为了验证FSSC算法的有效性，本文在Indian pines数据集上进行实验，图2展示了Indian pines的地面真实情况和对比算法的聚类图。从图2可以看出FSSC算法的聚类图更接近Indian pines数据集的真实情况。

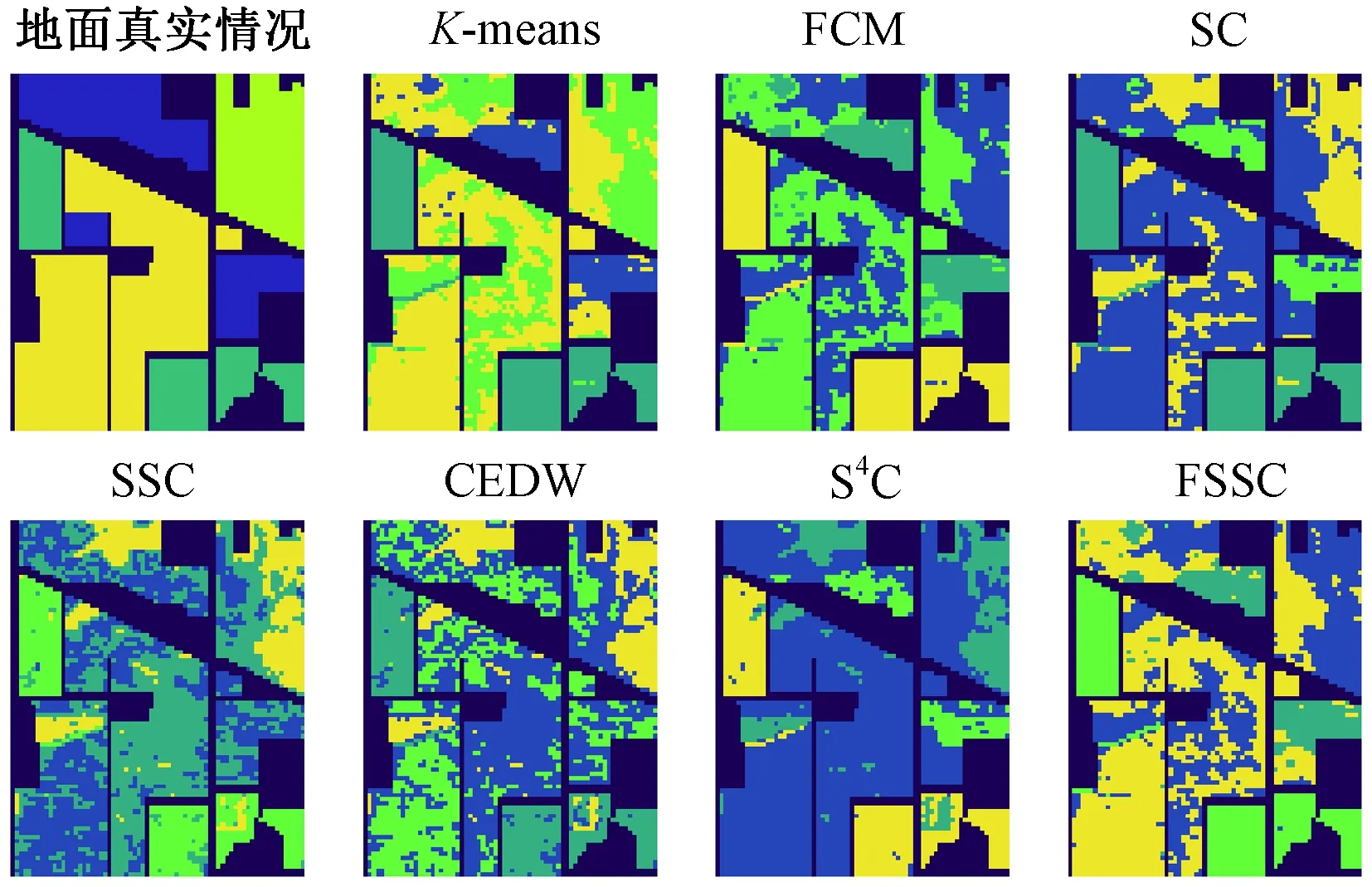
图2 Indian pines在不同算法下的聚类结果Figure 2 The Indian pines clustering results with different algorithms

表1展示了数据集不同算法对Indian pines各类地物的聚类精度。可以看出，FSSC算法在Corn_no_till的UA值比S4C提升了约40%，达到了62.69%。表2展示了Indian pines数据集在不同算法下的OA值和Kappa值，其中OA值达到了73.63%，在SSC和S4C的基础上分别提高了17.88%和4.92%，Kappa值则提高到了0.623 3。

3.3.2KSC数据集聚类结果分析 为进一步评估FSSC算法的有效性，本文还在KSC数据集上进行相应的实验。图3展示了该数据集的地面真实情况以及不同聚类算法下的聚类图。从图3可以看出，FSSC算法下的聚类图更接近KSC数据集的地面真实情况。

表1 Indian pines 图像在不同聚类算法下的UA值Table 1 The UA value of Indian pines image with different clustering algorithms 单位：%

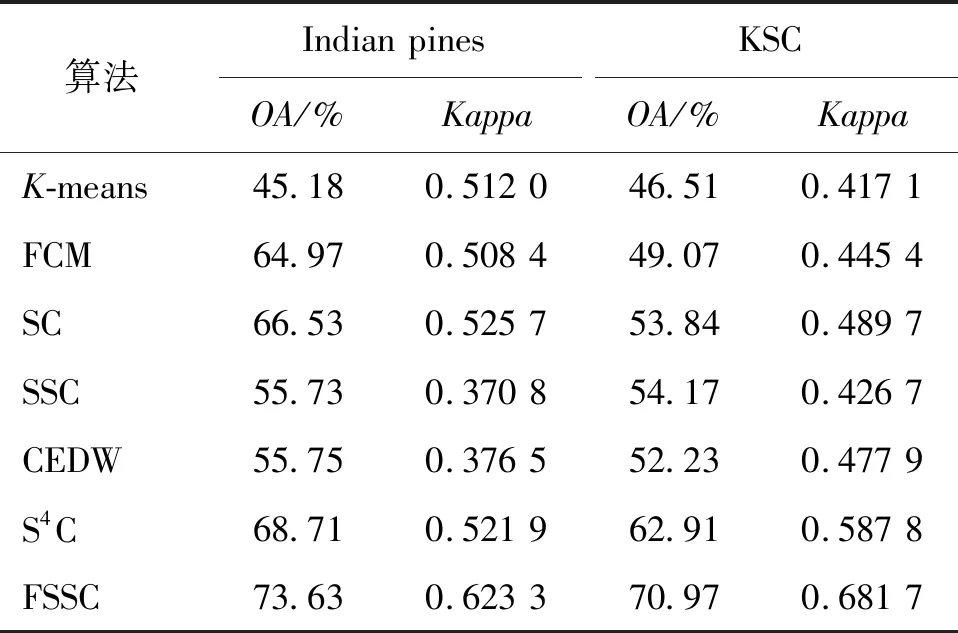
表2 Indian pines 和KSC图像在不同聚类算法下的聚类精度表Table 2 The clustering accuracy evaluation of Indian pines and KSC with different clustering algorithms

表3展示了不同算法下对KSC数据集各类地物的聚类精度，可以看出FSSC算法在Willow swamp的UA值达到了99.18%，并有效区分了Hardwood这一类别，UA值达到了65.07%。Salt marsh和Mud flats的UA值与SSC相比分别提高了40.58%和16.5%。该数据集的OA、Kappa值见表2，可以发现，FSSC算法的OA值达到了70.97%，在SSC和S4C的基础上分别提高了16.80%和8.06%，Kappa值提高到了0.681 7。以上实验表明，弗雷歇距离度量的相似度矩阵充分利用了HSIs的光谱信息,使实验的整体分割精度得到了提升。

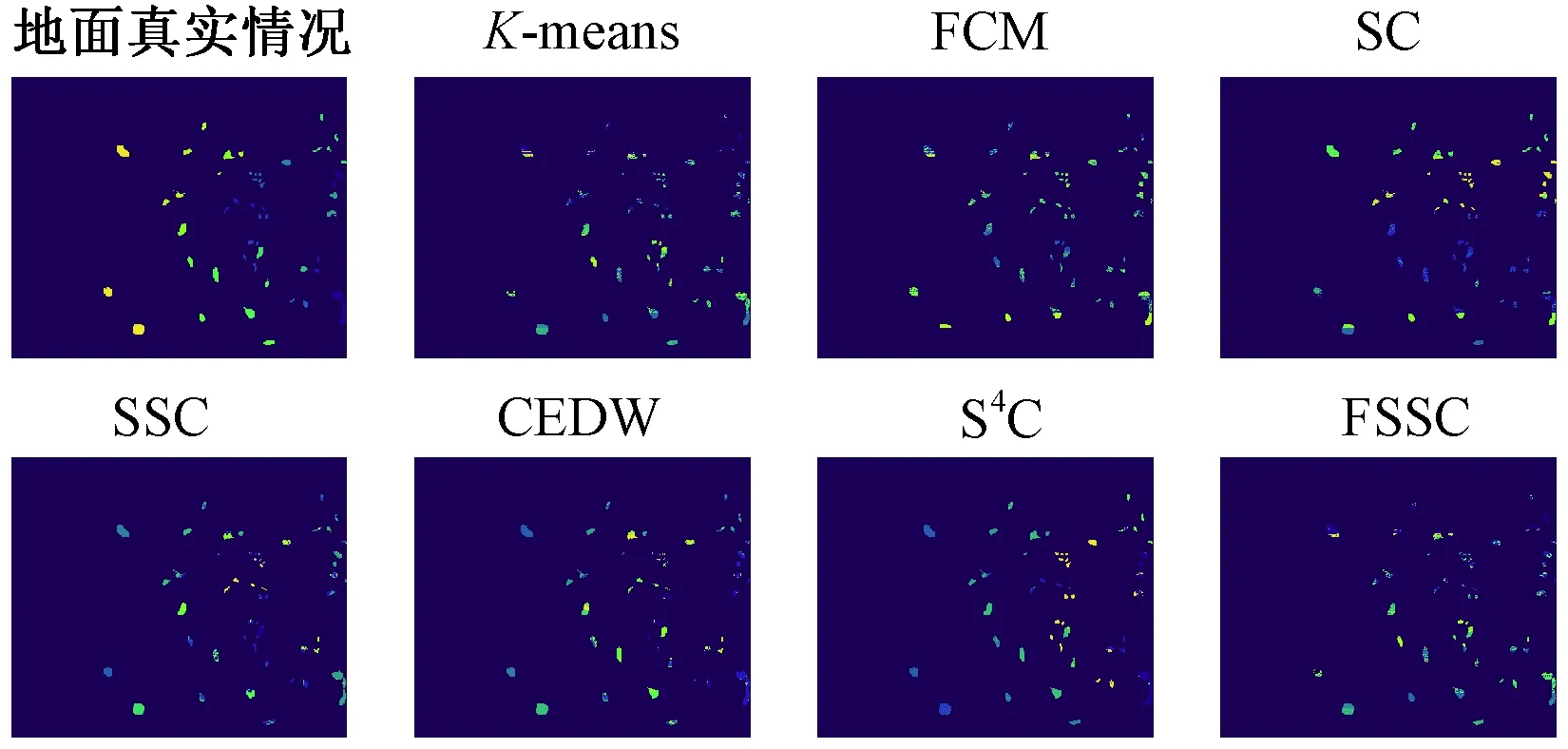
图3 KSC在不同算法下的聚类结果展示Figure 3 The KSC clustering results with different algorithms

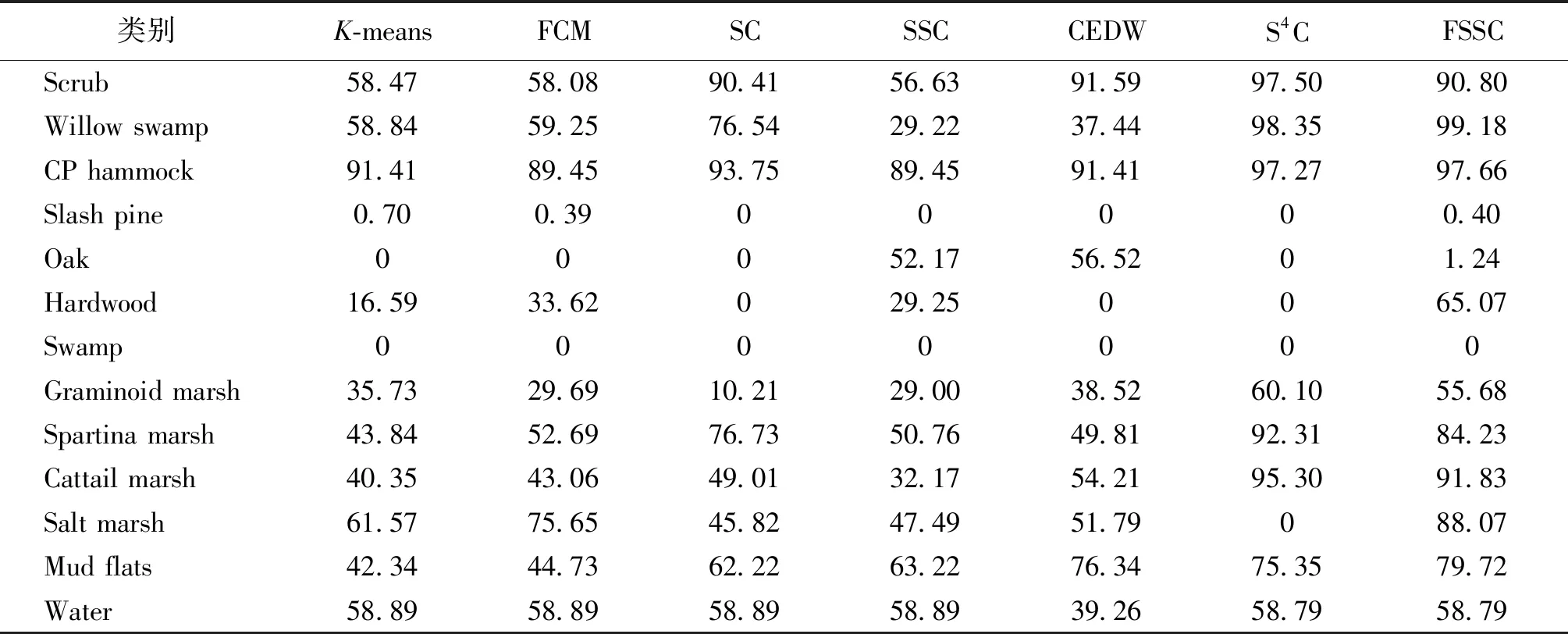
表3 KSC 图像在不同聚类算法下的UA值Table 3 The UA value of KSC image with different clustering algorithm 单位：%

4 总结与展望

针对稀疏子空间聚类算法在HSls分割中的缺点，本文提出了一种基于弗雷歇距离的HSls稀疏子空间聚类的相似矩阵构造方法(FSSC)。通过引入弗雷歇距离度量，克服了传统的SSC很容易受到欧几里得域中的噪声数据和异常值的影响。利用像素点光谱曲线之间的相似性构建相似度矩阵，并建立了光谱加权稀疏子空间聚类模型，基于稀疏系数矩阵和相似度矩阵重构邻接矩阵，更好地探索了HSIs的光谱结构信息。在两个HSIs数据集上的实验结果表明，FSSC算法明显优于现有的稀疏子空间聚类及一些改进算法。