模糊Kripke结构的子模型修复算法

王 辉，石铁柱，钱俊彦，潘海玉

(1.桂林电子科技大学 广西可信软件重点实验室 广西 桂林 541004；2.南京航空航天大学 计算机科学与技术学院 江苏 南京 210000)

0 引言

模型检测[1]被广泛运用到计算机系统、通信协议等方面的验证中，成为保证计算机系统正确性和可靠性[2]的重要手段。随着计算机系统的日益复杂和庞大，系统中存在的不确定信息使传统的模型检测不能对这类系统进行有效的分析和验证。因此，人们提出了基于模糊逻辑[3-4]的模糊模型检测、基于概率理论的概率模型检测[5-6]等。

模型检测的思想[7]是对模型的有穷状态空间进行遍历，检测系统模型是否满足规定的性质。如果模型不满足所检测的性质，算法会生成一个反例[8]来呈现模型中不满足性质规约的部分，但无法进行自动修复。如果需要修复系统，常需要设计人员进行手工分析和调试，导致效率低下，增加系统成本。

早在1999年，Buccafurri等就注意到模型无法自动修复这个问题[9]，为此提出了模型修复这个概念，并且提出一个模型修复算法，能够自动地通过修复模型中的结构，使模型满足性质规约。文献[10]首次提出了基于“可容许”模型的模型修复算法，对CTL检验的模型修复问题进行了深入的研究。Carrillo等[11]更加完美地解决了CTL的模型修复算法，在以往的模型修复中增添了“保护”的概念，并且提出了对应的算法。Attie等[12]提出了另外一种模型修复算法，该算法采用子模型修复，在只考虑删除状态和迁移关系的前提下，构造一个布尔公式，然后用SAT求解器来进行修复。在概率模型检测中，模型修复问题也得到了比较充分的研究[13-14]。

众所周知，模糊模型检测是系统量化验证[15-16]的一个重要研究方法，是经典模型检测理论[17]和模糊逻辑思想相结合而产生的，主要解决模糊系统的验证问题。在模糊模型检测中，系统被建模为模糊Kripke结构[18](fuzzy Kripke structures，FKS)，系统所需要满足的性质规约常用模糊计算树逻辑(fuzzy computation tree logic，FCTL)公式刻画。模糊模型检验已经在模糊离散事件系统[19-20]等方面取得了许多研究成果。然而，模型修复问题在模糊模型检测中还没有得到充分的重视。

文献[12]研究了CTL模型修复中的子模型修复，通过删去Kripke结构中的某些状态和迁移关系来构造子模型，从而达到修复的目的。本文对FCTL模型修复中的子模型修复问题进行讨论，将FKS中状态和模糊迁移的删去或保留规约为一个模糊命题逻辑公式，该模糊命题逻辑公式的可满足赋值对应着一个子模型。同时，本文给出了子模型修复算法，该算法利用模糊tableaux方法[21]求解模糊命题逻辑公式的可满足赋值，并且分析了算法的时间复杂度，给出算法正确性的证明。本文依据模糊逻辑的特点，提出带有模糊属性的命题公式，将CTL中的子模型修复方法推广到FCTL中。

1 子模型修复

下文出现的模型M、M′和Mi都是指模糊Kripke结构，简称为FKS。

为了便于相关讨论，下面给出FCTL子公式的定义。

定义1给定FCTL公式φ，其子公式集合sub(φ)归纳定义为

sub(p)={p}，p∈AP，

sub(p)={p}，p∈AP，

sub(φ1∨φ2)={φ1∨φ2}∪sub(φ1)∪sub(φ2)，

sub(φ1∧φ2)={φ1∧φ2}∪sub(φ1)∪sub(φ2)，

sub(EXφ)={EXφ}∪sub(φ)，

sub(AXφ)={AXφ}∪sub(φ)，

sub(EGφ)={EGφ}∪sub(φ)，

sub(AGφ)={AGφ}∪sub(φ)，

sub(Eφ1Uφ2)={Eφ1Uφ2}∪sub(φ1)∪sub(φ2)，

sub(Aφ1Uφ2)={Aφ1Uφ2}∪sub(φ1)∪sub(φ2)，

FCTL公式φ的长度|φ|=|sub(φ)|。

例如，由定义1得，A(p)U(q∨r)的子公式集合为{A(p)U(q∨r),p,p,q∨r,q,r}。

接下来给出子模型修复的具体定义。

定义2称M′=(S′,S′0,R′,AP,V′)是FKS，M′是M的子模型，记为M′M，如果以下条件成立：

1)S′⊆S,S′0⊆S0；

2) 对所有s,s′∈S′,R′(s,s′)=R(s,s′)；

3) 对于所有的s∈S′,p∈AP,V′(s,p)=V(s,p)，称M关于FCTL公式φ和阈值α∈(0,1]是子模型α-可修复的，如果存在M′M，使得φ(M′,s)≥α。

为了进一步研究子模型之间的关系，我们给出以下定理。

定理1子模型关系()是一个偏序关系。

证明设Mi=(Si,S0,i,AP,Ri,Vi)，i=1,2,3。

本文将FKS中状态和模糊迁移的删去或保留规约为一个模糊命题逻辑公式repair(M,φ,α)，现在给出子模型修复中该公式的构造方法。设M′=(S′,S′0,R′,AP,V′)是M的子模型，V是repair(M,φ,α)的一个赋值，用来计算修复后FSK的M′。

定义3如果满足条件

S′={s:s∈S,V(Xs)=1}，

S′0={s0:s0∈S0,V(Xs0)=1}，

R′={R(s,t):V(Es,t)=1,V(es,t)≥α}，

V′={V(s,p):s∈S′,p∈AP}，

称M′是repair(M,φ,α)公式在赋值V下的解，记为model(M,V)。

公式的解释如下。

Xs:设s∈S,s∈S′当且仅当V(Xs)=1；

Es,t:设s∈S,t∈R(s),R′(s,t)>0当且仅当V(Es,t)=1；

es,t:设R(s,t)>0,R′(s,t)≥α当且仅当V(es,t)≥α；

下面给出公式repair(M,φ,α)的构造方法和子模型修复算法SubModel-Repair。在子模型修复过程中，首先要保证得到的子模型在它某个初始状态对FCTL公式是α-可满足的。然后，给出repair(M,φ,α)中不同子公式的定义。

定义4设s∈S，t∈R(s)，φ是FCTL公式，阈值α∈(0,1]。repair(M,φ,α)由下面所有命题公式的合取构成。

∨s0∈S0Xs0。

(1)

对所有的s0∈S0，Xs0,φ。

(2)

(3)

(4)

对所有的p∈AP且V(s,p)≥α，Xs,p。对所有的p且V(s,p)≤1-α，Xs,p。

(5)

(6)

(7)

∨t∈R(s)(Es,t∧es,t∧Xt,φ1)。

(8)

∧t∈R(s)(Es,t∧es,t∧Xt,φ1)。

(9)

(10)

对所有的Aφ1Uφ2∈sub(φ)，m≤|S|，

(11)

对所有的EGφ1∈sub(φ)，m≤|S|，

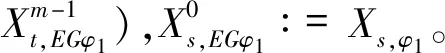
(12)

对所有的AGφ1∈sub(φ)，m≤|S|，

(13)

通过定义4可以构造一个模糊命题逻辑公式φ，该公式由某些模糊命题逻辑公式的合取构成，这些命题功能解释如下：式(1)要求子模型在初始状态所对应的公式是可满足的；式(2)～(4)要求子模型是FKS；式(5)～(13)要求出现的每个子公式都是α-可满足的。我们可以用模糊tableaux方法[21]来求解这个命题逻辑公式φ。值得一提的是，模糊tableaux方法是命题逻辑公式tableaux方法的扩张，可以用来解决模糊命题逻辑公式的可满足性。

对于图1中子模型，设FCTL公式φ为AGq，阈值α=0.3。以此为例给出一个具体的repair(M,φ,α)构造出的模糊命题逻辑公式φ。

图1 子模型示例图Figure 1 Sub-model example diagram

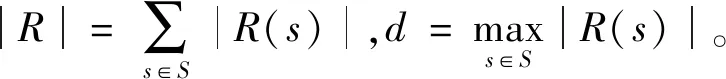
证明定义4构造了一个模糊命题逻辑公式φ，这个公式是一系列子公式的合取，通过每个子公式的具体构造方法，来分析整个构造过程的时间复杂度。

定义4中式(1)需要遍历每个s0∈S0，所以时间复杂度是O(|S0|)。同理，式(2)的时间复杂度也是O(|S0|)。式(3)需要遍历每个s∈S及其所有的后继状态，所以这种情况的时间复杂度是O(|S|×d)。式(4)要求遍历每个迁移，故时间复杂度为O(|R|)。定义4中式(5)要求考虑每个状态上的原子命题的值，因此时间复杂度是O(|S|×|AP|)。式(6)和式(7)要求遍历每个状态和每个子公式，故得到时间复杂度是O(|S|×|φ|)。定义4中式(8)和式(9)需要遍历每个子公式、每个状态和对应的后继状态，所以时间复杂度是O(|S|×|φ|×d)。式(10)最多需要m次遍历，其中1≤m≤|S|，每次要求遍历每个子公式、每个状态和对应的后继状态，所以时间复杂度是O(|S|2×|φ|×d)。同理，式(11)～(13)的时间复杂度是O(|S|2×|φ|×d)。

基于以上分析，定义4构造φ的时间复杂度是O(|S|2×|φ|×d+|S|×|AP|+|R|)。

算法1SubModel-Repair

输入:FKS的M，α∈(0,1]，FCTL公式φ。

输出:如果FKS的M可修复，则返回修复后的子模型M′，否则返回FALSE。

2) 对φ使用模糊tableaux方法，可以得到一个赋值V

3) ifV是一个可满足的赋值

4) returnmodel(M,V)

5) return FALSE

定理3设模糊命题逻辑公式φ运行模糊tableaux方法的时间复杂度为O(T(|φ|))，则算法的时间复杂度为O(|S|2×|φ|×d+|S|×|AP|+|R|×|φ|+T(|φ|))。

证明根据现有的模糊模型检测算法[5]，可知算法第1)步的时间复杂度是

O((|R|+|S|log|S|)×|φ|)。

根据定理2可知，算法第2步的时间复杂度是O(|S|2×|φ|×d+|S|×|AP|+|R|+T(|φ|))，整个算法的时间复杂度是O(|S|2×|φ|×d+|S|×|AP|+|R|×|φ|+T(|φ|))。

以下命题用来阐述repair(M,φ,α)公式的性质，这个性质可以用来证明算法SubModel-Repair的正确性。

证明对ξ用结构归纳法[22-23]来证明此命题成立。这里只给出当ξ=p,φ1∨φ2,EXφ1,Eφ1Uφ2时，这几种情形的具体证明过程。因为其他情形与这些情形的证明类似，故省略它们的证明过程。

当ξ=φ1∨φ2时，设V(Xs,ξ)≥α。根据定义4中的式(6)知，V(Xs,φ1)≥α或V(Xs,φ2)≥α。根据归纳假设知，

当ξ=EXφ1时，设V(Xs,ξ)≥α，即V(Xs,EXφ1)≥α。根据定义4中式(8)知，

V(∨t∈R(s)(Es,t∧es,t∧Xt,φ1))≥α，

(14)

(15)

同理，此时V(Es,t)=1，将V(Es,t)=1代入式(15)中，可以得到两种情形：

1)V(Xs,φ2)≥α；

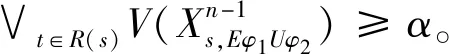
接下来分别对这两种情形进行讨论。

通过上述结论，可以证明算法是正确的，如果子模型M′是通过repair(M,φ,α)公式和model(M,V)所确定的，那么子模型M′一定是α-可满足的。

2 实例

本节通过一个医疗诊断和治疗[24-25]的例子来论证我们的结果，进一步阐述我们工作的潜在应用价值。

假设在某个地区出现了一种新的传染病毒。医院决定先会诊，安排一些医生制定一个治疗方案。医生们对这个病毒还没有完全地掌握和了解，但是根据经验觉得某些治疗手段(比如氧疗措施、口服抗病毒的药物治疗、中西医结合治疗等)会对这种传染病有较好的疗效[26]。下面我们利用一个FKS的M模型对这个治疗过程进行建模[27]。

为了方便叙述，我们把治疗过程建模为6个阶段，在图2中表示为6个状态，即

S={s0,s1,s2,s3,s4,s5}。

医生粗略地将病人的身体情况分为三种状态“poor”、“normal”和“good”，分别表示病人的身体状况“较差”、“一般”和“较好”。医生在考虑病人的呼吸、心跳、血压、体温和白细胞计数等生理特征后，再根据个人的经验，给出病人身体情况的综合评价。因为医生要考虑带有模糊性的不同因素，所以用状态上的模糊赋值表示病人身体的综合情况，具体如何给出模糊综合评价，可以参考文献[17]，如何给出模糊赋值可以参考文献[26]。为了方便阐述，本文简单给出表1的模糊赋值，表中的数值表示原子命题在对应状态上成立的程度。

图2 医疗诊断的FKSFigure 2 The medical diagnosis FKS

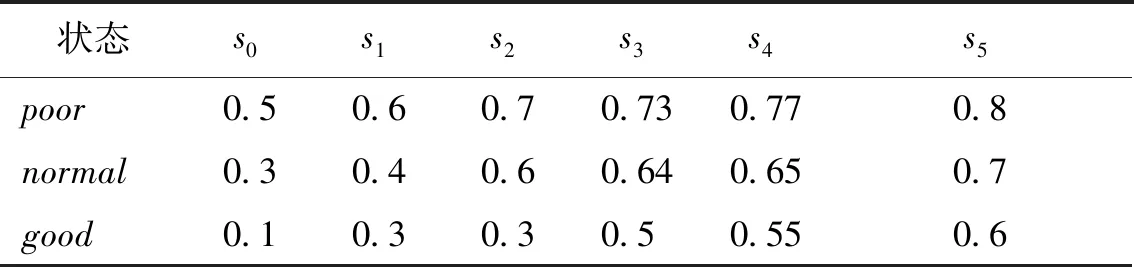
表1 模糊赋值函数表Table 1 Fuzzy valuation function table

通过一些治疗手段后，病人的身体状况会有所好转，即FKS当前状态转移到下一个状态。医生通过他们的经验[28]对状态之间转移的可能性进行估计，这些转移可以用一个矩阵R表示。