关于纵波能量的分析
2023-01-06张国锋
周 越,张国锋
(1. 北京林业大学 理学院,北京 100083;2. 北京航空航天大学 物理学院,北京 100191)
根据振动方向和传播方向的关系,机械波可分为横波和纵波. 横波的振动方向与传播方向相垂直,在介质中产生交替出现的波峰和波谷,与波形曲线一致,比较清晰直观;纵波的振动方向与传播方向相平行,在介质中产生交替出现的密部和疏部. 与横波相比,纵波的振动传播过程比较抽象,仅靠静态的图像不易讲清楚. 纵波的能量是学生疑问较多的内容,例如,直观上密部中的能量密度要比疏部中的大,而在普通物理教材中给出的能量密度分布以半波长为周期,并未体现介质密度变化的影响;再如,在纵波中有一半的体积元运动方向是和能流方向相反的. 本文详细讨论了纵波中的能量密度分布和能流的成因,以澄清这些疑问.
1 教材中对简谐波能量的处理
普通物理教材在讨论机械波的能量问题时,一般考虑一列平面简谐行波:
y=Acos(ωt-kx+φ)
(1)
在介质中取一个体积元dV,当波通过体积元传播时,体积元在平衡位置附近振动,因而具有动能:
(2)
由于各体积元的振动相位不同,会使介质发生形变,因而具有弹性势能[1]:
(3)
对于固体中传播的机械纵波,Y表示杨氏弹性模量.将式(1)代入式(2)和式(3),并利用Y=ρu2和k=ω/u等关系,可得
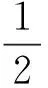
(4)
因此单位体积介质包含的波动能量即能量密度可表示为
(5)
波的传播伴随着能量在介质中的流动,这一特性可以由能流描述.由式(5)可知,介质中的能量分布是整体向x轴正方向平移的,且速度就是简谐波的波速u.如果取一个垂直于波传播方向的截面S,则在dt时间内通过S的能量是体积Sudt内所包含的波动能量.因此,单位时间内垂直通过S的能量即能流可以表示为
P(x,t)=w(x,t)Su
(6)
2 纵波的能量密度按实际空间位置的分布
根据式(5),能量密度在空间中呈周期分布,周期是简谐波波长的一半. 但如果考察介质中体积元的分布和运动状态,可以发现在纵波中能量密度的实际分布并非如此. 如图1,取一个整周期的波形,波形曲线如下方所示. 平衡位置位于a、c、e的体积元在最大位移处,无形变且振动速度为0,因此无波动能量;平衡位置位于b、d的体积元恰好经过平衡位置,振动速度和形变均最大,波动能量取极大值.但由于纵波的振动方向与传播方向平行,体积元实际位置和平衡位置的x坐标一般并不相同.例如,平衡位置在a、c、e的体积元实际上分别位于a’、c’和e’处,a’、c’和e’才是真正能量密度零点.因此,相邻两个能量密度零点间距不是λ/2,而是λ/2-2A和λ/2+2A相间排列.此外,纵波的传播会产生交替分布的密部和疏部,a、c间的介质被压缩到a’、c’之间,对应于密部;c、e间的介质被拉伸到c’、e’之间,对应于疏部.如果将最大位移处的体积元视为密部和疏部的边界,每个密部和疏部包含相等的波动能量,但密部的总体积小于疏部,这说明密部比疏部中的对应点(即振动相位相差π的体积元)应具有更大的能量密度. 总之,要想精确地描述介质中能量密度的分布情况,必须考虑体积元实际位置与平衡位置的差别以及介质中的密度分布.
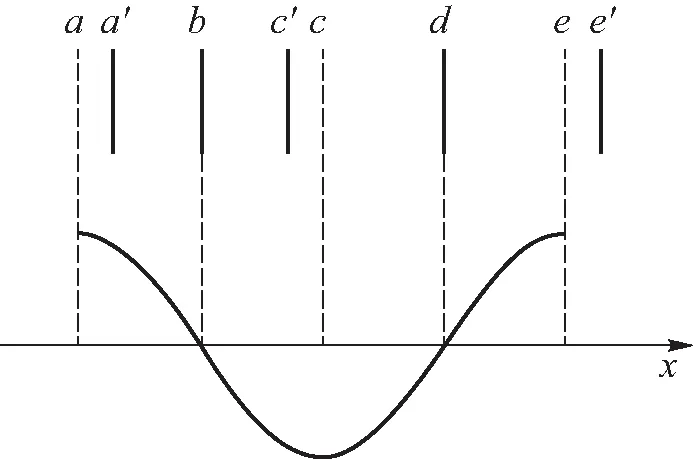
图1 波形曲线与体积元的实际位置
首先考虑密度变化的影响,在介质中垂直于波的传播方向隔离出原长为dx的一个薄片,其左侧和右侧截面平衡位置的坐标分别为x和x+dx.当波通过这段介质时,左侧和右侧截面处的位移分别是y和y+dy.这时,原长dx的介质薄片长度变为dx+dy,如果忽略垂直方向的形变,则该处介质的密度为
(7)
对于线性波,不会出现后方的体积元追上前方体积元的情况,这要求kA<1.将式(5)中的ρ用式(7)代替,可得
(8)
式(8)表示平衡位置为x的体积元所在位置的能量密度.
平衡位置为x的体积元在t时刻的实际位置是
x′=x+Acos(ωt-kx+φ)
(9)
可以把x表示为x′和t的函数
x=f(x′,t)
(10)
f(x′,t)的意义是,在t时刻位于x′处的体积元的平衡位置坐标.f(x′,t)无法用解析法表示,但从式(9)不难得出,f(x′,t)是关于t的周期函数,且周期等于简谐波的周期T.利用式(10)可以把能量密度表示为x′和t的函数,即
(11)
w′(x′,t)即能量密度按实际位置的分布,其在一个波长内的曲线如图2中实线所示,窄而高的峰对应于密部的能量密度分布,宽而低的峰对应于疏部的能量密度分布,两个峰宽度与高度的比例关系取决于A/λ.作为比较,w(x,t)的分布曲线以虚线表示,其两个峰的宽度和高度均相等.当A<<λ时,f(x′,t)≈x′,kA<<1,式(11)过渡到式(5).因此,式(5)实际是在振幅远小于波长的条件下对纵波能量密度分布的近似表示.

图2 能量密度的空间分布(A=0.1λ)
3 纵波的能流
在介质中,各体积元的振动状态在空间中以u的速度传播,波动能量也应以相同的速度传播.如果把ωt-kf(x′,t)+φ=const.看作x′关于t的隐函数,不难证明dx′/dt=u.因此式(6)仍然成立,只需将w(x,t)替换为式(11)中的w′(x′,t),即
P(x′,t)=w′(x′,t)Su=
(12)
P(x′,t)在一个周期内随时间的变化曲线如图3中实线所示.由能流的定义可知,P(x′,t)的变化规律与图2中能量密度分布曲线以波速u向右平移时,在某一x′处被截得的值变化规律相同.
下面具体分析能流的组成和成因.要维持波在介质中的传播,波源一侧必需有持续的能量输入.在波传播的过程中,介质的每个体积元将对下游的体积元做功,这产生了向下游传播的能流.如在x′处取一垂直波传播方向的截面S,则由做功产生的能流等于截面S左侧对右侧介质的功率:
P1(x′,t)=F(x′,t)v(x′,t)
(13)
平衡位置为x的介质对右侧单位面积介质的作用力,可以表示为[2]
(14)
则对于坐标为x′的垂直截面S,此作用力为
F(x′,t)=-YSkAsin[ωt-kf(x′,t)+φ]
(15)
在该截面处,体积元的振动速度为
v(x′,t)=-ωAsin[ωt-kf(x′,t)+φ]
(16)
这里应特别指出的是
(17)
式(17)右侧给出的是出现在x′处(不同的)体积元的位移随时间的变化率,而不是位于x′的体积元在时刻t的振动速度.将式(15)和式(16)代入式(13)可得
P1(x′,t)=YSωkA2sin2[ωt-kf(x′,t)+φ]
=ρω2A2Susin2[ωt-kf(x′,t)+φ]
(18)
由于对截面右侧介质的作用力总是与其振动方向一致,因此P1(x′,t)≥0.P1(x′,t)在一个周期内随时间的变化如图3中虚线所示,包含宽窄不同的两个峰,较窄的峰为截面处于密部时产生.由于密度的宽度较疏部窄,在一个周期中截面处于密部的时间小于半个周期.但是,截面处于密部和疏部中心时截面两侧相互作用力和截面处介质的振动速度大小都是相等的,相应地相互作用的功率也相等,因此两个峰具有相同的高度.

图3 能流的时间分布(A=0.1λ)
文献[2]、[3]中认为P1(x′,t)就是通过介质的全部能流,其实也是在波长远大于振幅时的一种近似.对于纵波,体积元的运动方向与截面S垂直,在平衡位置附近振动的过程中可能穿过截面,其所携带的能量也会穿过截面,这同样对能流有贡献.在S处,由体积元自身运动产生的能流为
P2(x′,t)=w′(x′,t)Sv(x′,t)
(19)
代入式(8)和式(16)可得
(20)
P2(x′,t)的曲线如图3中的点横线所示,由于体积元可以从任何一侧穿过截面,因此P2(x′,t)既可为正,也可为负.由图1可以看出,当截面S位于密部时,体积元从左向右穿过截面,P2(x′,t)为正;截面S位于疏部时则相反.由于密部的宽度比疏部小,在简谐波的一个周期中P2(x′,t)为正的时间小于半个周期.但密部中的体积元具有较大的能量密度,在一个周期中从两个方向穿过截面的体积元携带的总能量相等.因此P2(x′,t)只会改变能流的瞬时值,而对平均能流没有影响.P2(x′,t)对瞬时能流影响的大小取决于A/λ,如波长远大于振幅,由于|P2(x′,t)|∝A3而|P1(x′,t)|∝A2λ,因此|P2(x′,t)|<<|P1(x′,t)|,这时可以近似地把P1(x′,t)作为通过介质的能流.
介质中总的能流等于两种机制产生的能流之和:
P(x′,t)=P1(x′,t)+P2(x′,t)=
(21)
这样再次证明了式(12).可以看到,虽然体积元自身的运动可以产生一个向x轴负方向传播的能流,但其绝对值小于同一时刻由体积元间做功产生的能流,因此总的能流恒为非负,在任意时刻能量输运的方向均与平面简谐波的传播方向一致.
4 纵波的平均能量密度和平均能流
简谐波能量密度和能流都随时间周期性变化,在不关注瞬时值时一般可在简谐波的一个周期内求其平均.一个周期内通过截面的能量等于底面为S,高为λ的柱体包含的波动能量.结合图1可以看到,实际位置间距为λ的两个体积元,其平衡位置间距也是λ,不受介质压缩和拉伸的影响.因而在计算一个波长内的总能量时,利用式(11)与式(5)得到的结果是相同的,相应地两者的平均值也相同.下面直接对式(11)求平均来验证这一结论.由于S和u都不是时变的,故有
(22)
其中T=2π/ω.定义
(23)
可以证明
(24)
由定积分的性质可得
(25)
注意到g(x′,t)的第二项和第三项均以T为周期,当t=0和t=T时等值,因此
(26)
与由式(5)和式(6)式导出的平均能量密度和平均能流相同.
5 总结
对纵波而言,普通物理教材中给出能量密度和能流是在振幅远小于波长时的近似表达式,当振幅较大时应考虑介质压缩和拉伸引起的密度变化,以及体积元实际位置和平衡位置间的差异;能量密度和能流在一个周期内的平均值不受这些因素的影响.在纵波中能流有两个来源:其一是介质中体积元之间的功;其二是携带波动能量的体积元自身的运动,后者可能与波的传播方向相反,但在介质中总的能流总是指向波的传播方向.
