关于随机误差处理的一点讨论

张智明

(1. 广东理工学院 大学物理实验中心，广东 肇庆 526100；2. 华南师范大学 广东省量子调控工程与材料重点实验室，广东 广州 510006)

大学物理实验课是理工类专业大学生进入大学后的第一门实验课，基础性强，涉及的专业和人数较多. 狭义地讲，它能帮助学生加深对物理学本身的理论和原理的理解. 广义地讲，它对培养学生严谨的科学态度和学风、较强的动手能力、细心的观测能力以及对实验结果的归纳、整理和分析能力等具有不可替代的作用. 基于此，《大学物理实验》教材在科学上的严谨性、在逻辑上的自洽性就显得非常重要. 然而，笔者在教学中发现，不少教材中存在着这样或那样的问题. 本文旨在讨论其中的一些问题.

1 存在的问题

为了下面的叙述方便，先引入若干相关概念.设待测物理量为X，其真值为x0.在相同的条件下对物理量X做多次(N次)重复测量(即所谓的等精度测量)，测得一组值{xk}(k=1,2,…,N)(称为测量列).在这个测量列中，第k次测得值xk的误差为

δk=xk-x0

(1)

X的算术平均值为

(2)

下面列举一些在《大学物理实验》教材[1-5]中关于随机误差处理的一些问题.

问题1:在许多《大学物理实验》教材中有如下表述：测量列{xk}的随机误差由下列标准方差描述:

(3)

但未解释为什么要用这个量来描述.

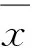
(4)

当用残差vk代替误差δk时，标准偏差σ的表达式变为(称为贝塞尔公式)

(5)

(6)

许多教材中既没有给出公式(5)和(6)的证明，也没有引用相关文献.

问题3:在许多《大学物理实验》教材中有如下表述：最常见的一种随机误差服从正态分布(高斯分布)，其概率分布函数的表达式为

(7)

其中误差δ和标准偏差σ分别为

δ=x-x0

(8)

(9)

[注：式(9)即为式(3)，但为了讨论方便，这里重写了一遍].式(8)中的x为物理量X在连续变化情况下的测量值.显然，由式(7)到式(9)的表述是不自洽的，因为式(7)和式(8)是连续变量(x连续变化)的形式，而式(9)是离散变量(xk不连续变化)的形式.

下面将依次给出对问题1的回答,给出式(5)和式(6)的证明,给出问题3的自洽描述.

2 对问题1的回答

如上所述，对测量列{xk}(k=1,2,…,N)，第k次测得值xk的误差δk由式(1)描述.对随机误差，xk可以等于、大于、或小于x0，从而δk可以等于零，也可正可负、可大可小，是完全随机的，因此，当测量次数N足够大时，可以合理地认为，误差{δk}的平均值：

(10)

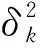
(11)

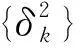
3 式(5)的证明

式(1)和式(4)相减可得

(12)

(13)

(14)

(15)

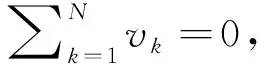
(16)

由式(14)得

(17)

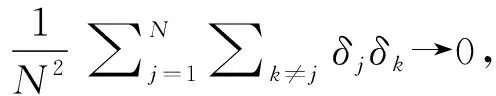
(18)

将式(18)代入式(16)得

(19)

利用方差的定义式(11)，上式变为

于是得

(20)

4 式(6)的证明

首先介绍误差传递公式[6-8]：设F是多个自变量{xk}的函数F({xk})，则F的标准偏差为

(21)

其中σxk是每个自变量xk的标准偏差.这就是误差传递公式.

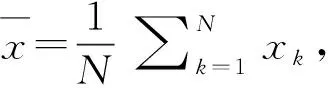
(22)

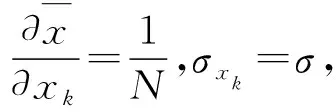
(23)

这正是式(6).该式表明，适当增加重复测量的次数，可以减小测量误差.

5 关于问题3的讨论

现在考虑在测量列{xk}(k=1,2,…,N)中有相等测得值的情况.设在N个测得值中有M(M≤N)个不同的测得值xj(j=1,2,…,M)，且xj出现nj次，则算术平均值可写为

(24)

(25)

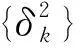
(26)

当测量次数N→∞时，过渡到测得值x连续变化的情况(连续变量情况).定义测得值x的概率分布函数(概率密度)p(x)为测得值落在x附近单位区间的概率，则测得值落在区间x→x+dx的概率为p(x)dx.显然，概率分布函数应满足归一化条件：

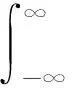
(27)

在连续变量情况下，误差、算术平均值、方差、标准偏差分别定义为

δ(x)=x-x0

(28)

(29)

(30)

(31)

现在回到问题3.相关内容[式(7)到式(9)]的自洽表述应该如下[式(32)到式(35)]：最常见的一种概率分布是所谓的正态分布，也称为高斯分布，其函数形式为

(32)

或

(33)

其中

δ(x)=x-x0

(34)

(35)

表1给出了连续变量情况和离散变量情况下的若干对应公式，以供参考.

表1 离散变量和连续变量情况下的若干对应公式

6 结束语

本文讨论了在《大学物理实验》教材中用于描述随机误差的若干概念的物理意义，给出了用于随机误差处理的若干公式的证明，纠正了一些教材中关于正态分布的不自洽表述.