考虑研磨子—车轮和轮轨作用的城际动车组车轮磨耗预测
2023-01-04赵长雨沈正行温泽峰
赵长雨,赵 鑫,王 鹏,沈正行,温泽峰
(西南交通大学牵引动力国家重点实验室,四川,成都 610031)
近年来,我国轨道交通发展迅猛,交通网络已覆盖绝大部分领土,截止2020 年底,高速铁路总运营里程近3.8 万千米,城际轨道交通也已列为“新基建”核心内容之一。开放环境中服役的轮轨系统,其接触界面易受到雨、雪、油污和树叶等污染,或引发轮轨间低黏着问题[1],导致车轮空转和滑行等现象。为清理车轮表面污染物,高速和城际列车均采用研磨子改善轮轨界面服役环境[2]。研磨子安装在车轮上方,与车轮相对位置关系如图1 所示。在检测到车轮发生空转、滑行时,或速度大于30 km/h 的制动工况下,研磨子会动作[3],保证轮轨间黏着水平。

图1 研磨子与车轮相对位置Fig. 1 Relative position of tread trimmer and wheel
列车服役中发现,研磨子除了保证轮轨间黏着,也具有抑制车轮多边形[4]、滚动接触疲劳[5]和踏面凹坑磨耗[6−7]等效果。但是,当高硬度研磨子频繁、长时、高压作用于车轮时,也会造成踏面磨耗速率过高的副作用,例如,运行站间距短的城际动车组上曾发现研磨子和车轮使用寿命过低的问题,大大增加了运维成本[8]。因此,有必要就研磨子造成的车轮磨耗开展研究,为研磨子的优化设计提供理论支撑。
车轮磨耗[9]一直是轨道交通研究的关键内容之一,常采用试验、仿真和线路跟踪等多种研究手段[10],磨耗预测模型多采用ARCHARD[11]及基于摩擦功[12]和磨耗指数的磨耗模型[13]等。JENDEL[11]建立了基于Gensys 动力学仿真和Archard 磨耗模型的车轮磨耗预测模型,分析了地铁车辆通过不同半径曲线和直线时的磨耗,并将不同半径路段所致磨耗按实际线路比例进行线性叠加,预测结果与实测总磨耗吻合较好。ENBLOM 和BERG[14]进一步发展了Jendel 的预测模型,在切向FASTSIM模型中考虑弹性应变项,用于更精确计算轮轨间滚动接触行为,提升了磨耗预测精度。LI 和KALKER[15]采用CONTACT 精确滚动接触理论和基于磨耗功的磨耗模型,建立了适用于多点、共形接触等非Hertz 接触工况下的轮轨磨耗预测模型。PRADHAN 等[16−17]通过Adams 动力学软件和Matlab 联合仿真的形式,基于Archard 磨耗模型模拟印度铁路网的车轮磨耗,并评估了车辆在不同车轮磨耗阶段的动力学响应。LI 等[18]采用车辆-轨道耦合动力学、三维非Hertz 滚动接触和Archard 磨损模型,建立了考虑列车动力学行为的车轮磨耗预测模型,并对比了两种磨耗累计方法,发现一个接触斑长度内采用多个接触斑信息的方法更精确。需强调,现有车轮磨耗预测均专注于轮轨接触界面所致磨耗,未将研磨子对车轮磨耗的贡献考虑在内,故不适用于装有研磨子且其作用频繁的城际动车组工况。
本文针对我国某型城际动车组,建立集车辆系统动力学模型、研磨子―车轮接触模型和车轮磨耗模型为一体的车轮磨耗预测模型,为深入研究研磨子的磨耗贡献提供基础工具。
1 车轮磨耗仿真模型
1.1 车辆系统动力学模型
以我国南方某城际线路上运行的某型城际动车组为例,应用SIMPACK 软件建立含50 个自由度的多体非线性车辆系统动力学模型,包含1 个车体、2 个构架、4 条轮对和8 个转臂。车体与构架通过二系悬挂连接,具体包括空气弹簧、抗蛇形减振器和横向减振器等,构架与轮对通过一系悬挂连接,具体包括钢弹簧、垂向减振器和转臂定位装置等,模型中减振器元件保留非线性特征。车辆系统动力学模型及关键参数取值如图2和表1 所示。

表1 我国南方某城际线路上运营动车组的关键参数取值Table 1 Values of key parameters of EMUs running on an intercity line in south China

图2 车辆系统动力学模型Fig. 2 Vehicle system dynamics model
上述城际线路全长116.12 km,曲线总长63.14 km,占比54.37%,表2 列出了该线路上不同半径曲线和直线路段的详细统计结果。半径小于2500 m 的曲线间隔500 m,之上间隔1000 m 分组统计,每一组路段长度为其半径范围内各路段长度总和,超高、缓和曲线长度和速度等均取其中长度最长的曲线段的实际值。各组中左、右曲线占线路总长的比值也列入表中,“−”表示没有对应项。这里忽略了坡道、道岔及进出停车场等线路信息。
于上述城际线路直线段、R450 m、R1200 m和R2200 m 圆曲线段上,测取的钢轨型面见图3。其中,内轨指曲线段低轨或直线段左轨,主要表现为轨顶磨耗,外轨指曲线段高轨或直线段右轨,其侧磨随着曲线半径的增大而逐渐降低,半径大于2200 m 时侧磨消失,磨耗形式趋于直线段。

图3 不同半径曲线圆曲线段的实测钢轨廓形Fig. 3 Measured rail profiles on circular curves of different radii
为保证车轮磨耗仿真的计算精度,本文模拟了表2 中所有分组,且考虑左右曲线,共分析了15 条曲线和1 条直线,每条线路都以各组中长度最长的曲线段的实际半径进行计算,并施加了京津轨道谱。为方便计算,曲线(缓和曲线段加圆曲线段)全长取1200 m,缓和曲线段长度依表2 设定,剩余长度即为圆曲线段长度。受制于有限的实测钢轨廓形,R450 m 和R800 m 半径采用R450 m曲线段的实测钢轨,R1200 m 和R1600 m 半径采用R1200 m 曲线段的实测钢轨,R2200 m 采用R2200 m 曲线段的实测钢轨,其余线路均采用直线段实测轨。

表2 我国南方某城际线路的曲线和直线统计情况Table 2 Statistics of curves and tangent tracks on an intercity line in south China
1.2 研磨子-车轮接触模型
忽略低黏着偶尔触发的研磨子作用,正常情况下列车从某车站运行至下一车站的过程中,研磨子仅在列车进站制动时作用一次。依此,可将两站间的车轮磨耗分成如下两个阶段。
1)列车制动前阶段,包括牵引、匀速运行段。期间车轮磨耗和廓形演化仅由轮轨接触决定。
2)进站制动直至完全停止阶段,此时,研磨子作用也对车轮磨耗和廓形演化有贡献。考虑到轮轨和研磨子作用所致磨耗分布不同,可大致将此段内的研磨子—车轮接触分成图4 所示的4 个状态(图中假设磨耗后研磨子与车轮接触,而非新研磨子)。初始状态a,阶段1)中轮轨接触所致车轮磨耗,使得刚开始作用时研磨子和车轮在名义滚动圆附近存在一定的间隙;最终状态d,研磨子作用结束后研磨子和车轮几何变得完全贴合,这是基于现场实测几何做出的合理假设;为大致模拟上述变化过程,加入了两个中间状态b 和c,用于定量模拟。

图4 研磨子与车轮接触面关系演化过程Fig. 4 Evolution of trimmer-wheel contact
初始状态a 的垂向间隙分布,根据文献[8]中轮轨接触所致车轮磨耗的估算结果设置。如图5 所示,实际中轮轨接触导致了踏面−31 mm~52 mm 范围内的近似山峰型磨耗分布,最大值为1.89×10−4mm,模型中初始状态a 的间隙简化为分布在±30 mm 范围内、幅值1.80×10−4mm 的分段三次拟合曲线,近似山峰型;最终状态d 的垂向间隙恒取零。中间2 个状态的间隙亦处理成分段三次拟合曲线,分布范围分别为±20 mm 和±10 mm,幅值取1.20×10−4mm和6.00×10−5mm,见图5。需说明,本文和文献[8]针对同一城际线路上相同动车组,均使用平均23.98 km 的站间距。

图5 研磨子和车轮接触面的垂向间隙分布Fig. 5 Distributions of vertical gap between trimmer and wheel tread
进一步假设每种状态的发生概率与相邻间隙曲线所围的面积(Si)成正比,图5 中S1∶S2∶S3=5∶3∶1。又假定状态d 发生概率与状态c 相同,则模拟分析中状态a~状态d 发生概率比取为5∶3∶1∶1。
考虑上面4 种间隙状态,建立了图6 所示的研磨子—车轮接触有限元模型,接触界面上采用了尺寸1.00 mm 的精细网格,采用基于罚函数法的“面-面”算法进行接触计算,非接触区域的网格尽可能稀疏处理[19]。计算时,在与车轴相配合的轮毂内表面节点上施加全约束。表3 列出了模型中使用的车轮和研磨子材料参数,研磨子相关参数由根据文献[2]和文献[20]中测量结果推演得到。

表3 车轮和研磨子材料参数Table 3 Material parameters of trimmer and wheel

图6 研磨子—车轮接触有限元模型Fig. 6 A finite element contact model between trimmer and wheel tread
现实中踏面清扫器由列车气源提供动力,相连的气动装置将出闸压力作用在研磨子背部,将研磨子压到车轮踏面上。研磨子出闸压力与气动装置工作气压关系为:

式中:F/N 为出闸压力;弹簧复位力F0取100 N;气缸直径d取40 mm;P/MPa 为工作气压;效率η取95%。
理想状态下出闸压力均匀作用在研磨子背部,但实际上研磨子相对于车轮易发生横向相对转动,导致如图7 所示左偏载、均载和右偏载三种典型工况。图7 中第一行为三维压力分布示意图,总力等于研磨子出闸压力,第二行为yz截面内压力分布示意图,左、右偏载下均假设压力从零线性增加。分析中考虑了此三种工况,且假设发生概率比为1∶1∶1。

图7 研磨子的三种出闸压力分布Fig. 7 Three pressure distribution on a trimmer
综合考虑4 种研磨子—车轮接触状态和研磨子3 种压力分布形式,则有12 种工况组合。基于上述概率假设,每种工况的发生概率见表4。
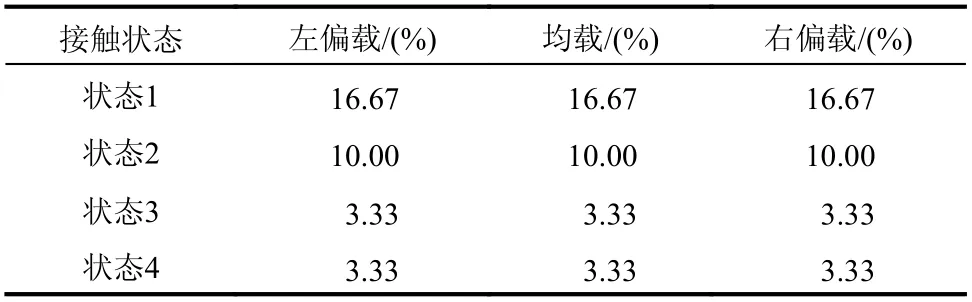
表4 研磨子—车轮接触的12 种工况及发生概率Table 4 12 contact cases between trimmer and wheel tread and their occurrence probabilities
1.3 车轮磨耗模型
轮轨接触和研磨子—车轮接触所致车轮磨耗均采用Archard 磨耗模型计算,即磨耗体积与法向力和滑动距离的乘积成正比,与材料的硬度成反比,具体表达为:

式中:Vw为磨耗体积;kw为磨耗系数;N为法向力;d为滑动距离;H为车轮材料硬度。
轮轨接触所致车轮磨耗计算过程如下:将动力学模型中得到的轮轨接触斑划分为n×n个单元,任意时刻各单元的法向压力和相对滑移量分别由Hertz 理论和FASTSIM 求得;代入式(2),求得滑移区任一单元的磨耗深度为:
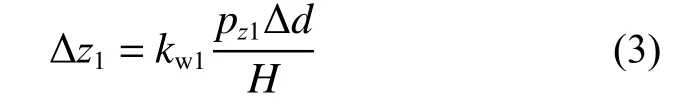
式中:∆z1为选取单元的磨耗深度;pz1为该单元处轮轨法向压力;∆d为其滑动距离;kw1取值与接触压力和相对滑动速度有关,具体参考文献[11]中磨耗系数分区取值(四个分区中kw1分别取350×10−4、4×10−4、35×10−4和5×10−4);H取车轮硬度280 HB。将各单元磨耗深度沿前进方向进行线性叠加,即假设轮轨接触状态在短时间内不变,可得到一次轮轨接触所导致的总磨耗深度。
研磨子表面单元可沿滚动方向分成126 列,如图8 所示,作用时依次通过任一车轮截面接触。研磨子所致车轮磨耗计算过程如下:研磨子任一列表面单元与某一车轮截面接触时,其所致该截面处的磨耗深度为:

图8 研磨子―车轮接触时的局部图Fig. 8 Zoom-in of the contact between trimmer and wheel tread

假设研磨子制动作用一次时车轮滚动m圈,则研磨子导致的车轮总磨耗深度为m∆z2。新研磨子两端存在倒圆,如图9 所示,A 和C 区域对车轮磨损作用弱于B 区域,故引入磨损比例系数ky(定义为研磨子磨损区域各位置与0 mm 位置处垂直距离之比,研磨子几何由其全寿命期内综合磨损情况确定,取为恒定),以修正研磨子几何造成的影响,即车轮截面最终的总磨耗深度为kym∆z2。研磨子工作气压小,作用在车轮表面的法向接触压力随车轮型面变化幅度小,故研磨子―车轮接触所致的磨耗始终采用同一车轮型面进行计算。

图9 研磨子几何变化及磨耗比例系数设置Fig. 9 Evolution of trimmer geometry and the setting of a wear coefficient
2 仿真计算流程
利用上述仿真模型预测车轮磨耗的大致流程示于图10 中,可分为如下三步:
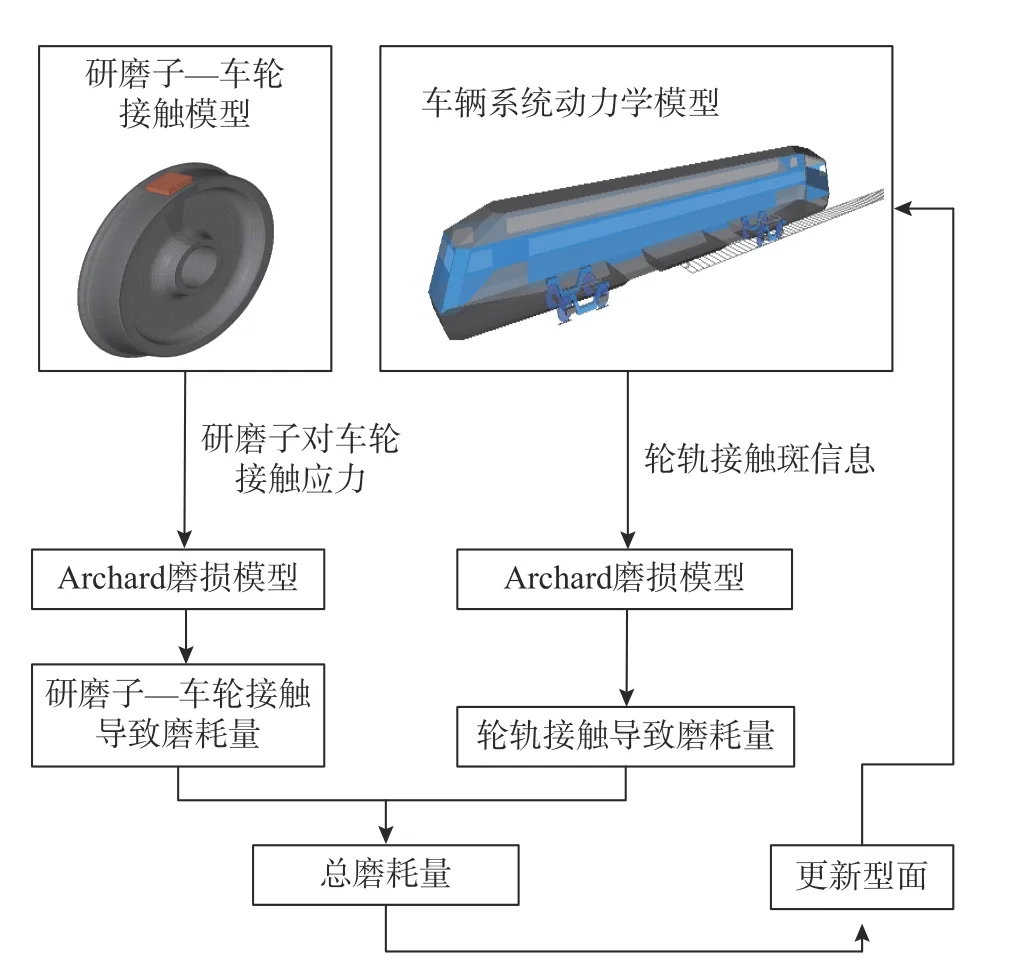
图10 车轮磨耗仿真计算流程图Fig. 10 A flow chart of wheel wear prediction
1)轮轨接触所致磨耗预测
采用车辆系统动力学模型,计算车辆通过不同半径曲线和直线工况下轮轨接触姿态和相应接触解,继而计算相应工况下车轮每旋转1 周所致车轮磨耗。按照表2 所示曲线占比,由不同工况下车轮磨耗得到一个站间距23.98 km 内所发生的总磨耗量。
2)研磨子―车轮接触所致磨耗预测
利用研磨子―车轮接触模型计算12 种工况下的车轮表面接触法向压力,继而算得各工况下车轮每旋转1 周时研磨子所致车轮磨耗,再根据每次制动时的研磨子与车轮相互作用距离和每种工况发生概率(表4)进行叠加,得到一次制动过程中研磨子―车轮接触所致车轮磨耗。
3)车轮型面更新
列车运行中,车轮型面演化的磨耗量是逐渐累积的结果。仿真计算时,当轮轨接触和研磨子所致车轮综合磨耗量的最大值累积到0.10 mm 时,即对车辆动力学模型中的车轮型面进行更新,更新时对磨耗后廓形施加三次样条插值平滑,保证可以计算。然后,重复上述过程,直到总里程数达到指定值,计算结束。需指出,整个过程中忽略了钢轨廓形变化。
另外,为减少计算量,仿真时车辆仅向一个方向运行,反向运行的车轮磨耗量直接取为正向时对应位置车轮的磨耗,即反向1 位轮、4 位轮对分别取正向4 位轮、1 位轮对上相同侧车轮的结果,2 位轮、3 位轮对也同样处理。
3 磨耗系数确定和模型验证
3.1 研磨子所致车轮磨耗系数确定
文献中关于研磨子所致车轮磨耗的研究匮乏,故式(4)中kw2数值未知。本节通过对比车轮磨耗的预测与实测结果,确定一个适用于本文所开发车轮磨耗模型的研磨子所致车轮磨耗系数kw2,具体如下。
利用上述建立的车轮磨耗预测模型,模拟文献[8]中城际动车组第一镟修周期内跟踪测试的LM 车轮廓形演化,模拟条件与实际运营情况相同,具体信息如下:车辆运行线路见表2;车辆系统动力学模型的初始车轮型面采用第一镟修周期内镟后里程为0 万千米时实测平均型面,研磨子-车轮接触模型的车轮型面同样采用上述实测平均型面;高硬度研磨子持续作用(列车速度从194 km/h降至30 km/h 期间,研磨子和车轮相互作用距离为4571.88 m),工作气压0.49 MPa;共模拟总运行里程16.52 万千米,12.68 万千米时车辆进行一次掉头。
图11 中黑色实线选自文献[8]中第一镟修周期内估算的研磨子所致车轮磨耗分布。采用试凑法,发现当kw2=1.45×10−4时,得到仿真结果与试验吻合良好,详见图11。

图11 研磨子所致磨耗试验和仿真对比Fig. 11 Comparison of measured and predicted wheel wear caused by trimmer
3.2 模型验证
依然考虑3.1 节中提到的镟修周期,预测了不同里程下的车轮廓形演化,具体为一节车厢8 个车轮的平均廓形结果,如图12 中虚线所示。为方便对比,图12 中也展示了实测的某动车组32 个车轮的平均廓形[8]。可见,同里程下仿真与实测廓形几乎重合,均在踏面−50 mm~52 mm 均发生磨耗;在52 mm~60 mm 处有轻微差异,预测磨耗稍小,这主要是仿真中未考虑车辆通过道岔等轮轨在该区域接触的工况[21]。需说明,这里展示8 个车轮平均廓形,旨在去除现场复杂多变运营工况导致的车轮磨耗随机性。

图12 不同里程下仿真和实测平均廓形对比Fig. 12 Comparison of measured and predicted average wheel profiles at different mileages
提取图12 中仿真和实测廓形名义滚动圆(踏面0 mm)处的磨耗量,进一步展示于图13 中。可见,预测和实测的磨耗量增长趋势基本相同,均随里程近似线性增长,试验和预测磨耗速率分别为0.20 mm/万千米和0.21 mm/万千米,相差仅5.00%。

图13 仿真与实测平均廓形名义滚动圆处磨耗量对比Fig. 13 Comparison of measured and predicted wheel wear at nominal rolling circle
综上,本文所建模型,可较准确预测研磨子频繁作用下城际动车组车轮的磨耗。
4 研磨子工作模式对车轮磨耗影响
文献[8]的试验证实研磨子工作方案是影响车轮磨耗的重要因素之一。利用上述建立的车轮磨耗模型,模拟了研磨子采用不同工作模式时LM车轮廓形的演化,为合理选取研磨子工作模式和延长车轮使用寿命提供支撑。
模拟具体信息如下:车辆运行线路见表2;车辆系统动力学模型的初始车轮型面采用LM 型面,研磨子-车轮接触模型的车轮型面同样采用LM型面;高硬度研磨子施加0.30 MPa 工作气压;考虑了图14 所示6 种工作模式,每种模式中上、下横线对应研磨子工作和停止工作状态,横坐标为车辆制动距离,模式1~模式5 为间歇工作模式,工作时间20 s,停止工作时间分别为25 s、20 s、15 s、10 s、5 s,以此周期作用,模式6 为持续工作模式。需说明,模式4 和模式6 已在工程实践中应用,另外4 种以模式4 为基础来设计。每种模式模拟总里程20 万千米,10 万千米时车辆进行一次掉头。
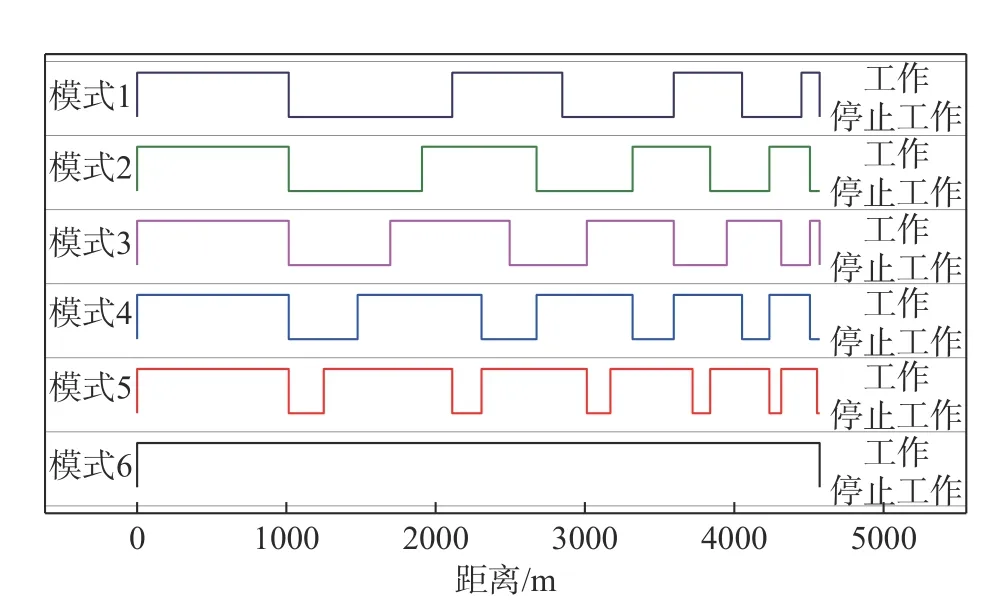
图14 研磨子6 种工作模式示意图Fig. 14 A schematic diagram of 6 working modes of trimmer
提取8 个车轮在5 万千米、10 万千米、15 万千米和20 万千米时踏面名义滚动圆处研磨子—车轮接触所致磨耗量、轮轨接触所致磨耗量和总磨耗量的平均值,发现三种磨耗量均随里程的增加而大致线性增加,线性拟合的磨耗速率如图15 所示。可见,从模式1~模式6,随着研磨子停止时间减少,研磨子—车轮接触和轮轨接触所致磨耗速率均提高,模式6 下总磨耗速率最大,为0.12 mm/万千米,是模式1(0.08 mm/万千米)的1.50 倍。

图15 名义滚动圆处三种磨耗速率Fig. 15 Wear rates at nominal rolling circle of wheel tread
图16 展示了不同运行里程下1 轴车轮的预测型面与60 N 轨匹配时等效锥度变化。可见,研磨子采用模式5 和模式6 时等效锥度均发生了显著下降,之后分别在0.08 和0.06 附近波动,而采用模式1~模式4 时,等效锥度随里程变化的趋势不明显,维持在0.10 附近,有利于车辆的长期运行稳定性。
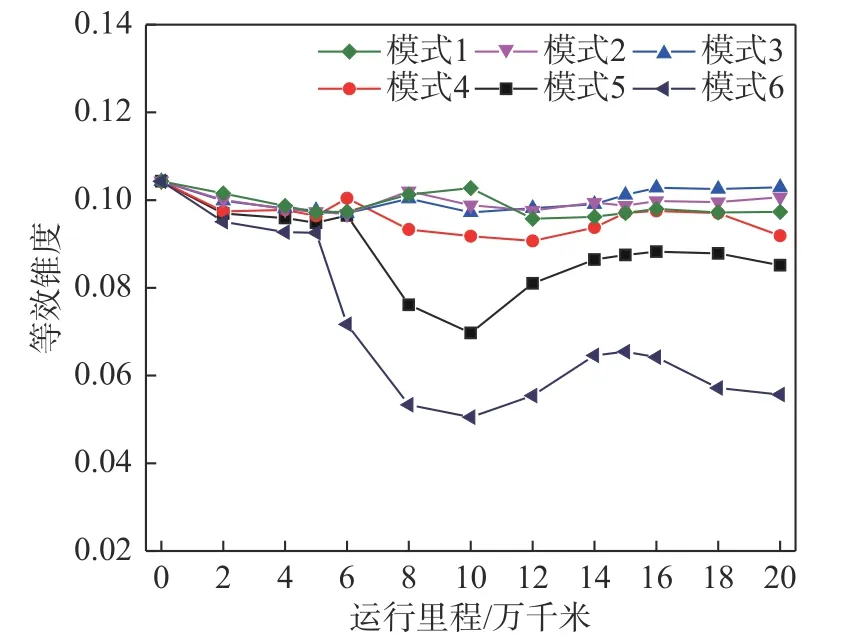
图16 1 轴车轮与60 N 轨匹配等效锥度变化Fig. 16 Variation of equivalent conicity when wheels of axle 1 match 60 N rail
另考虑到研磨子对车轮多边形的抑制作用,研磨子—车轮接触所致磨耗速率应不低于0.01 mm/万千米[22](图15 中虚线)。综合考虑,建议采用高硬度研磨子时,选用0.30 MPa 工作气压下工作20 s、停止25 s 的间歇式工作模式。
5 结论
针对站间距短、研磨子频繁作用的城际铁路,引入必要的研磨子—车轮间相互作用假设,建立了考虑研磨子—车轮和轮轨接触所致磨耗的动车组车轮磨耗预测模型,对比某城际动车组的车轮磨耗跟踪测试,完成了模型验证,并分析了研磨子不同工作模式的影响。得到主要结论如下:
(1) 采用Archard 磨耗模型计算研磨子—车轮接触所致车轮磨耗时,其磨损系数取1.45×10−4。
(2) 该模型可较准确地预测城际动车组服役车轮的廓形演化,磨耗预测误差5.00%左右,并可定量确定研磨子—车轮和轮轨接触的贡献。
(3) 针对模拟的城际铁路系统,发现采用0.30 MPa 工作气压和高硬度研磨子时,研磨子最佳工作模式为“工作20 s—停止工作25 s”的间歇式工作模式。
该模型为动车组研磨子系统的优化设计提供有效模拟工具。
