耦合电感型Zeta变换器的参数优化方法

徐邦贤，刘晓波，韩祥民，邱 知，唐 辉，范津玮

(1.贵州大学 电气工程学院，贵州 贵阳 550025； 2.国网舟山供电公司，浙江 舟山 316000)

非耦合电感型Zeta变换器的工作效率较高，具有升降压的特性，能适应输入电压宽范围的变化，因而在新能源光伏发电领域有着广泛的应用[1]。耦合电感型Zeta变换器输出电压纹波较非耦合电感Zeta变换器小，应用更加广泛。但耦合电感式Zeta变换器的频率特性复杂导致闭环控制器设计较为困难。文献[2～4]构建的Zeta变换器小信号模型，忽略了中间电容电压的动态特性，将中间电容电压建模为恒定值。但该电容的电压变化是导致右半平面零点形成的原因，因此忽略该电容电压变化将无法全面掌握系统的频率特性，也无法分析电路参数对变换器频域稳定性的影响。文献[5～8]建立了详细的Zeta变换器数学模型，但因没有分析电路参数与系统频率特性的关系以及与系统特征方程根的关系，故无法对电路参数进行优化。文献[9～10]建立了电压反馈型传统Zeta变换器电路状态空间平均模型，采用混沌理论分析了反馈系数对闭环稳定性的影响，但该方法没有体现变换器电路参数与系统频率特性的关系，因此无法进行参数优化。文献[11]采用切换建模的方法对传统Zeta变换器不同导通模式进行了统一建模，并且模型精确且有效，但该文献缺乏对电路参数与系统零极点位置的关系的分析，也没有各参数对系统频率特性的影响。文献[12]在高增益耦合Zeta转换器的小信号动态特性分析方面缺乏分析电路参数对系统频率特性的影响，一旦电路参数设计不恰当将会使得相频特性上产生较大的相位滞后，使得控制器设计困难，无法获得良好的动态特性。此外，该传递函数给出的是数值形式，无法体现电路参数与系统频率特性、零极点位置的关系。

文中建立了变换器从控制变量到输出电压的小信号传递函数，并提取了频率特性相关的参数。本文分析了电路参数对系统的稳定性、快速性的影响，以及频率特性与零极点位置的关系，并据此提出了参数优化设计的方法。最后，在变换器开、闭环状态下进行分析，并对比了优化前后系统的时域特性与频域特性，证明了所提设计方法的有效性与可行性。

1 变换器建模分析

耦合电感型Zeta转换器的电路图如图1所示。图中，L1、L2、C1、C2、M分别为输入电感、输出电感、隔直电容、输出电容、L1与L2之间的互感，rL1、rL2分别为输入电感与输出电感的等效串联电阻，rC1、rC2分别为隔直电容与输出电容的等效串联电阻，Uin、Uo分别为输入电压、输出电压，Io为输出电流，静态占空比D可由式(1)求得。

(1)

采用状态空间平均法[13]对图1电路进行建模，得控制变量c到输出电压uo的传递函数Gvd(s)，如式(2)所示。根据经典控制理论[14]，系统可划分为1个一阶微分环节、二阶微分环节，以及两个二阶谐振环节，其中fL为低频谐振的自然频率，fH为高频谐振自然频率，QL为低频品质因数，QH为高频品质因数，fn为微分环节谐振自然频率，Qz为微分环节品质因数。式(3)中的频率特性参数fL、fH、QL、QH、fn、Qz均是电路参数的函数，与电路参数的相关性较强，主导着变换器的频率响应特性。GPWM为调制器的增益，G0为功率级直流增益。

图1 耦合电感型Zeta转换器的电路图Figure 1. Circuit diagram of coupled inductor Zeta converter

(2)

式中

Δs)=

fL≈

fH≈

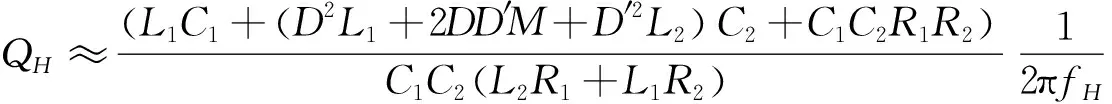
2 变换器的参数优化设计

2.1 耦合电感参数设计

如图1所示，耦合电感可以看做是1个耦合系数kc的单绕组变压器，kc与参数L1、L2、M的关系如下

(3)

优化该单绕组变压器的参数时，设初始电感L1、L2之间的比值为k1，电感L1与互感M的比值为k2，则电感L1、L2、互感M有如下关系。

L2=k1L1

(4)

M=k2L1=kck1L1

(5)

2.2 输出电容C2的参数设计

假定变换器需要5个开关周期才能开始调整输出电压，设电压下跌值为ΔV，输出电流突变值为ΔI，变换器的开关周期为Tsw，则C2的值为

(6)

变换器的控制器存在计算延迟[15]，在控制律计算的过程中，输出电流突增时，容易出现输出电压下跌的情况。由式(6)可知增大输出电容C2能够缓解因计算延迟引起输出电压下跌的程度。

2.3 系数k1对开环系统稳定性的影响

当Qz<0时，复零点从s平面的左半面移动到右半面，使得系统存在闭环不稳定的风险。为了将复零点限制在左半面，需使Qz>0，由式(4)、式(5)、Qz的表达式及由式(8)可知，电容C1的值应大于零，则k1的取值范围如下。

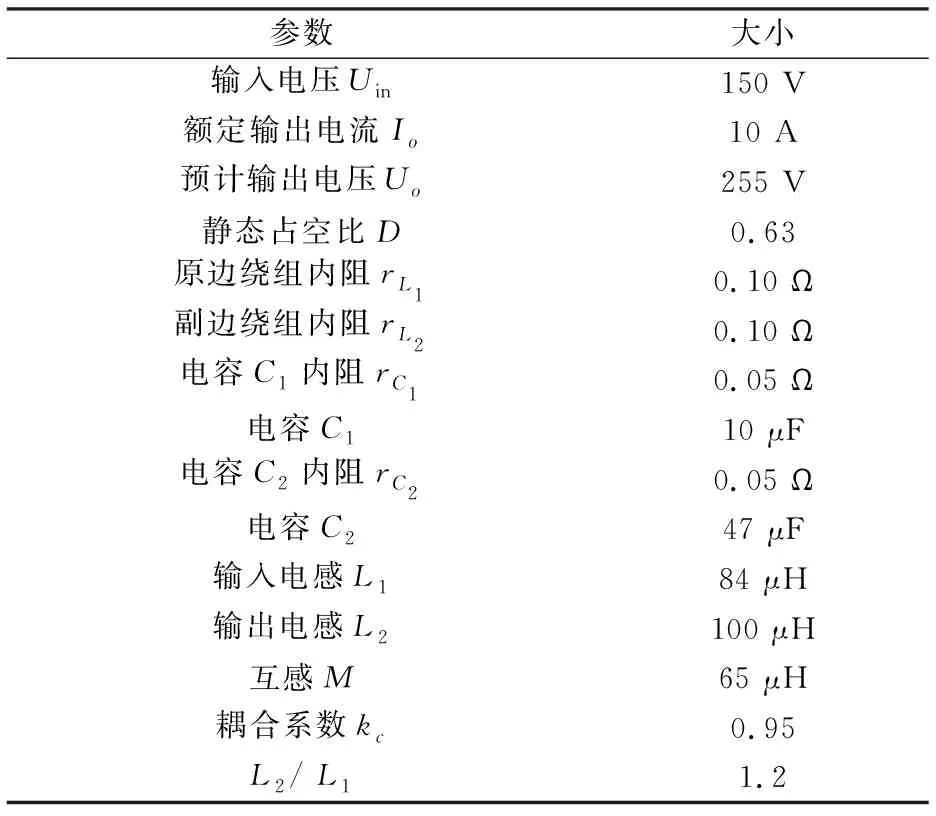
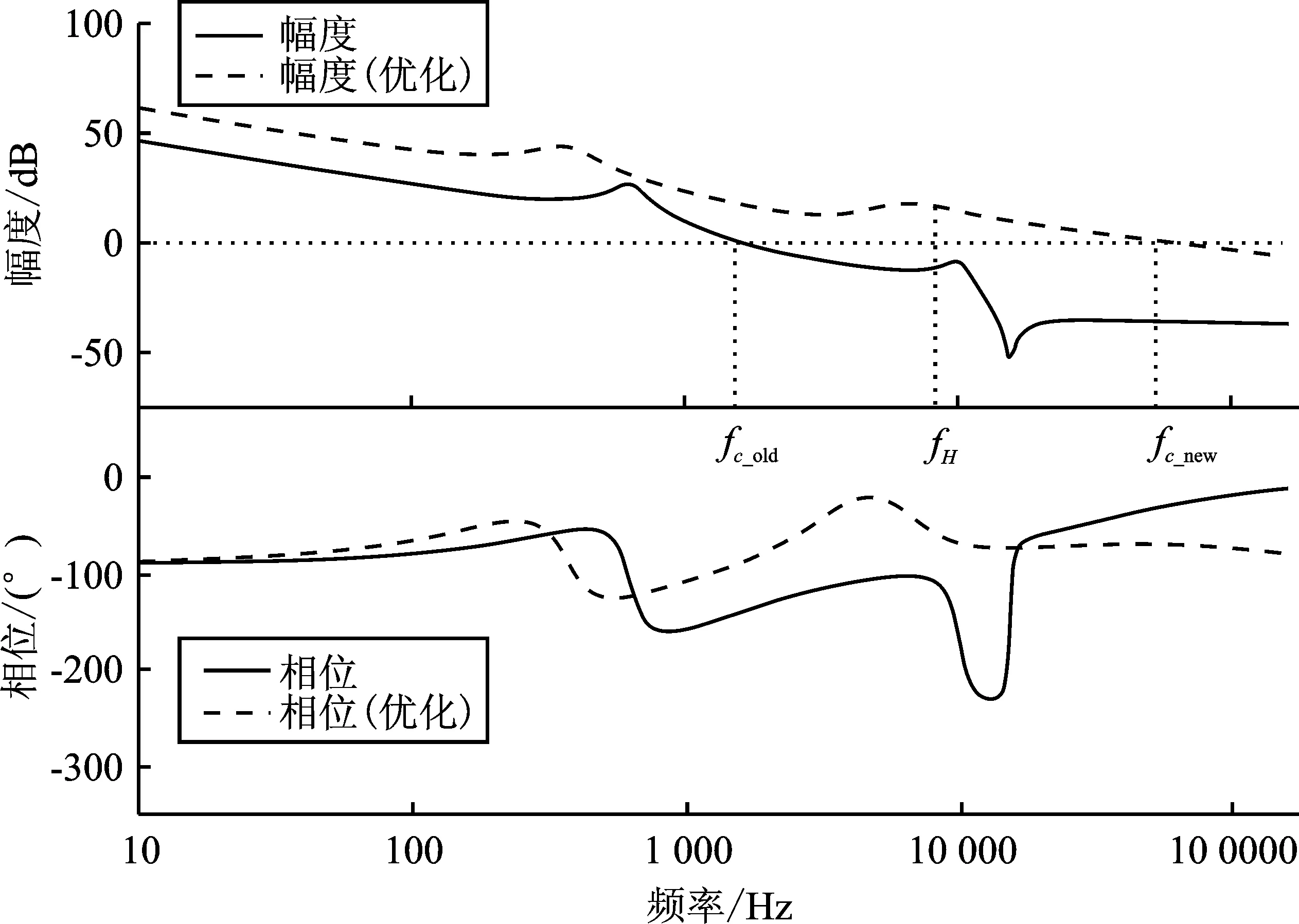
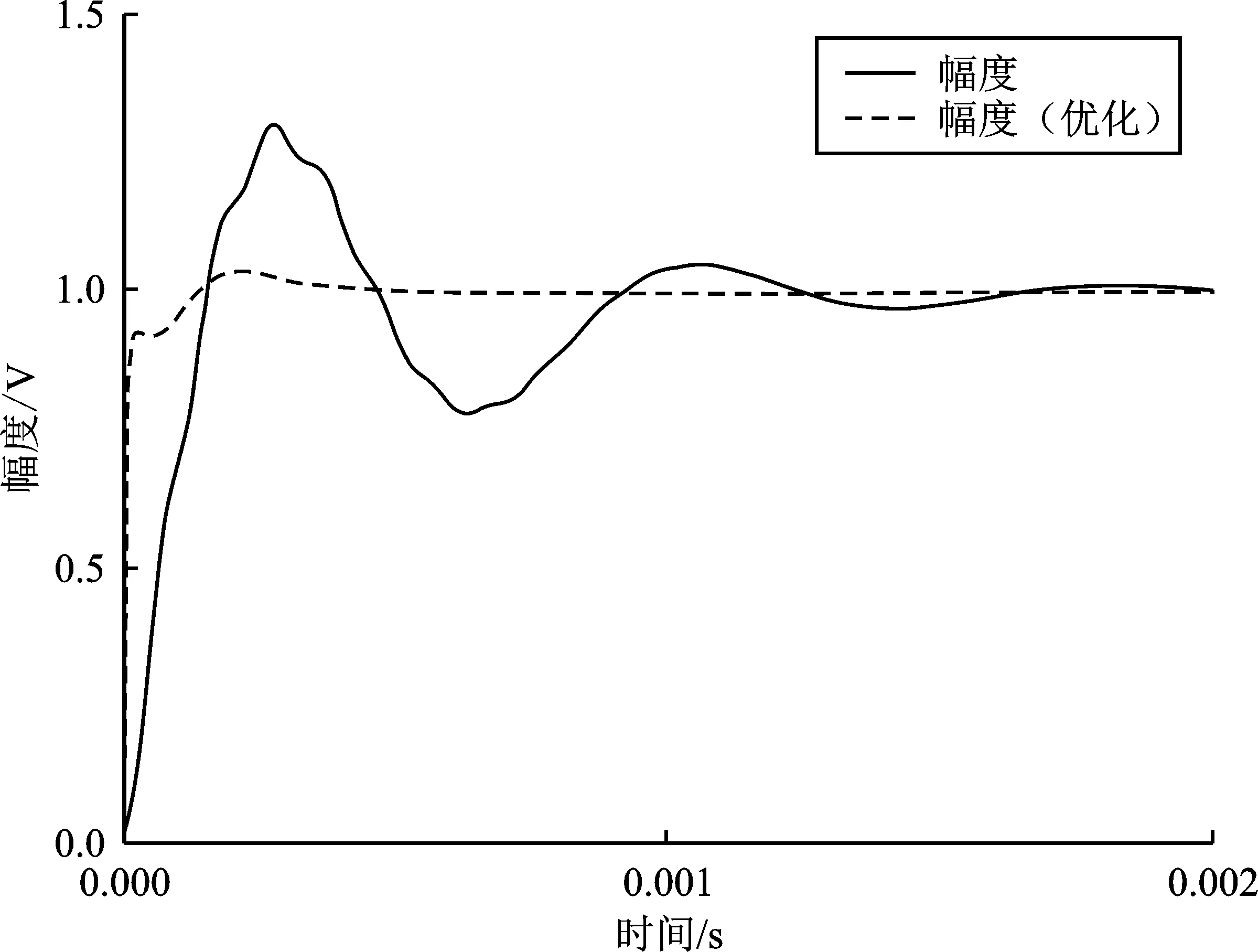
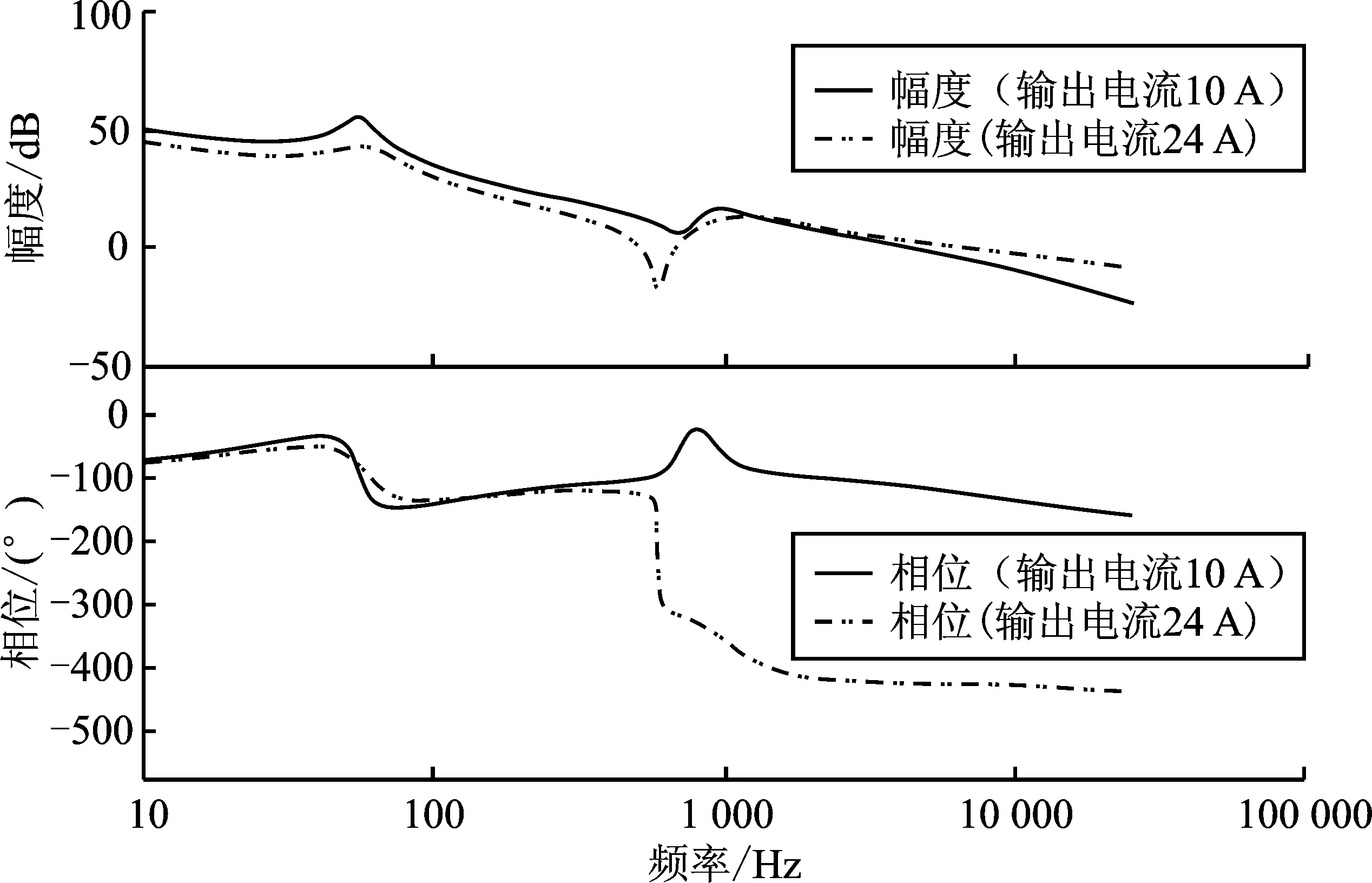
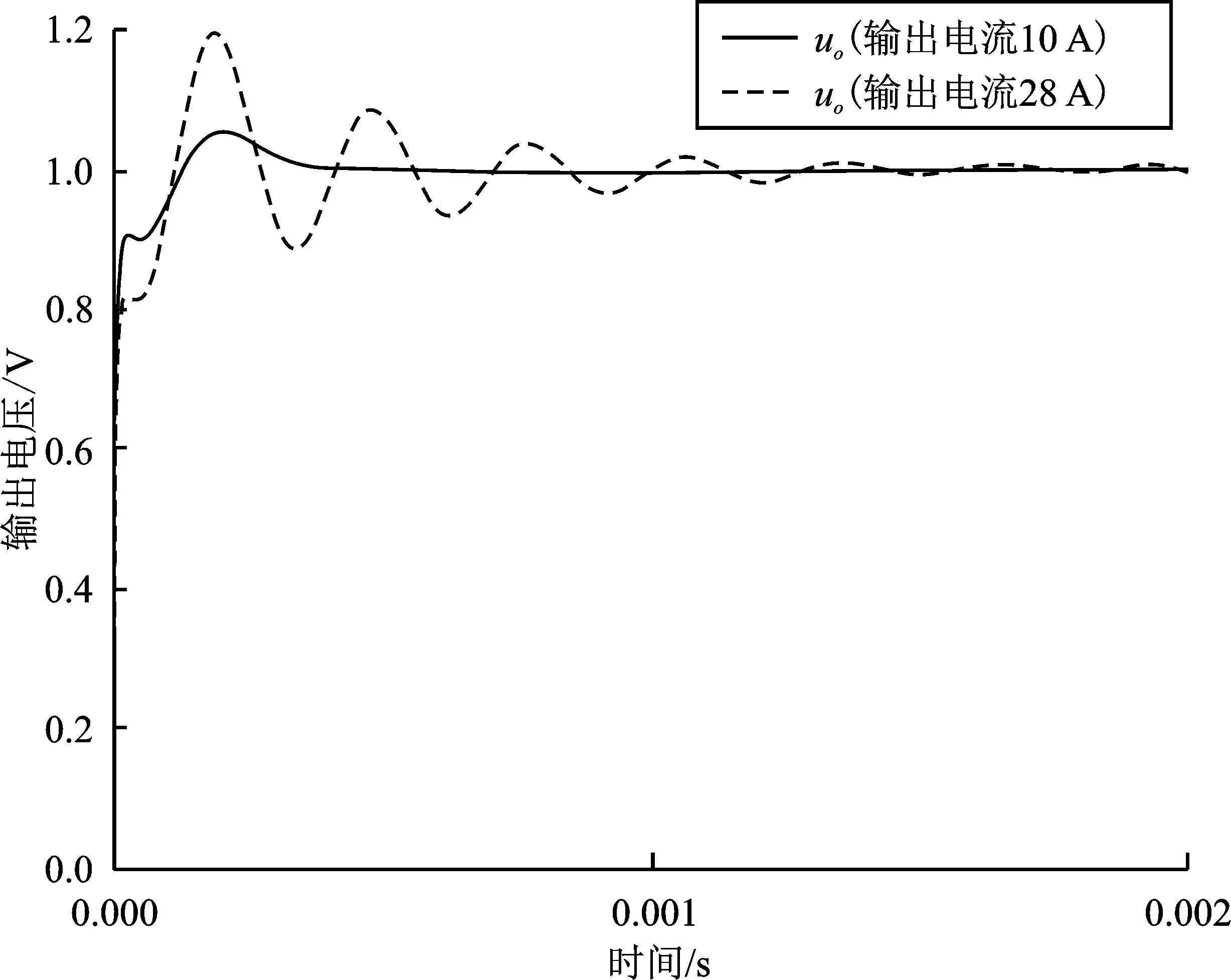
1≤k1

(7)

(8)

设输入电压Uin为150 V，输出电流为Io=2 A，静态占空比D为0.6，寄生参数rL1、rL2、rC1、rC2分别为0.1、0.1、0.05、0.05。由式(1)可知输出电压Uo为169.3 V。取电感L1= 84 μH，耦合系数kc= 0.95，由式(7)、式(8)得1

图2 k1 取不同值的零极点图Figure 2. Zero-pole graphs with different values of k1

2.4 隔直电容C1的设计

传递函数存在两对复极点，一个复零点和一个单零点。复极点能够在Gvd(s)的波特图的幅频特性曲线上产生峰值，在相频特性上产生180°的相位滞后，当控制器存在滞后环节(例如积分环节、一阶滤波环节)时，开环系统总的相位滞后将更严重。

此时，提高系统稳定性的途径是降低控制器的直流增益，降低闭环系统的带宽，但该方法无法保证系统的快速性。此外，也可选择对控制器加入更多超前补偿环节来增大控制器的响应延迟。

若满足条件fn=fH，则能够使系统的复零点靠近复极点，最大程度抵消一部分复极点给系统带来的高频峰值响应及过度的相位滞后，使系统的频率特性接近二阶系统的频率特性，降低了控制器设计的难度。令fn=fH，则C1如下所示。

(9)

2.5 参数设计方法的步骤

综上所述，所提方法的设计步骤如下文所述，其中待优化的电路参数有L2、M、C1、C2，具体步骤为：

步骤1采用原始输入电感L1、输出电感L2、耦合系数kc的值，根据式(4)、式(5)计算初始比值k1_init、互感M；

步骤2根据变换器斩波周期Tsw、期望的ΔV、ΔI，由式(6)计算输出电容C2的值；

步骤3根据给定的输入电压Uin、输出最大电流Io以及寄生参数rL1、rL2、rC1、rC2，由式(1)计算静态占空比D。此时，输入电感L1、输出电感L2、互感M、静态占空比D、输出电容C2的值已知，由式(9)计算C1的值。

步骤4由式(8)计算k1_max，判定初始比值k1_init是否满足式(7)的约束关系，若满足约束关系，则设计结束，无需对输出电感L2、互感M进行优化；若k1_init超出下限，k1_new取下限值；若k1_init超出下限，k1_new取上限值。根据式(4)、式(5)、原输入电感L1、k1_new重新计算输出电感L2、互感M的值。

此时，参数L2、M、C1、C2优化结束，具体设计流程见图3。

图3 电路参数优化流程图Figure 3. Flow chart of circuit parameter optimization

3 算例验证

3.1 变换器参数未优化之前的频率特性验证

本文采用表1变换器电路参数，代入传递函数Gvd(s)，采用MATLAB绘制未校正前开环系统的波特图。

表1 耦合电感型Zeta变换器的电路参数Table 1. Circuit parameters of coupled inductor Zeta converter

从图4中未校正的系统相频特性曲线可以看出，在截止频率fc处存在300°的相位滞后。

采用带二阶滤波的PID控制器验证所设计方法的可行性，PID参数采用MATLAB的Sisotools工具箱进行设计[16-17]。如图5实线所示，因开环系统的相位滞后较大，最高截止频率只能设计到fc_old处，约为1 kHz，可知没有足够的开环增益抑制控制环路内含频率成分为fH的扰动干扰，当控制环路存在含频率为fH的扰动信号时，如图6所示的输出阶跃响应曲线含有高频振荡成分，并且设定时间较长，过冲的幅度较大。由于实际情况中，负载的内阻是不断跳变的，导致输出电流也在不断跳变，振荡次数较多，因此输出电压将产生高频振荡群，对负载的寿命产生不利的影响，可见控制器的性能较差。

3.2 变换器参数优化后的频率特性验证

将表1的原始电路参数采用文中提出的方法进行优化，各参数如表2所示，并代入传递函数Gvd(s)，绘制Gvd(s)的伯德图。如图4虚线所示，截止频率fc基本不变，在fc处的相位滞后已减小至180°以内且高频处的谐振峰的作用被减弱，此时主要由低频复极点产生相位滞后。给功率级设计控制器时，可以将功率级看做是一个二阶系统，只需要对低频复极点处产生的相位滞后进行补偿，令fc处的增益大于20 dB即可衰减频率为fH的高频成分。

图4 变换器功率级开环波特图Figure 4. Bode diagram of open-loop of converter power stage

表2 耦合电感型Zeta变换器经优化的电路参数Table 2. Optimized circuit parameters of coupled inductor Zeta converter

如图5虚线所示，可见优化后的截止频率可提高至fc_new约为30 kHz，在频率fH处有足够的开环增益抑制控制环路内含频率为fH的扰动信号，使控制系统能快速跟踪参考信号。如图6虚线所示，系统的输出阶跃响应中的高频振荡成分完全消失，超调量大幅减小，达到稳态所需的设定时间缩短4倍，系统的响应速度较快，提升了控制器的性能。在负载频繁跳变的情况下，控制器能够及时减小输出电压下跌的幅度，保持输出电压恒定，避免高频振荡群对负载的寿命产生不利影响。

图5 校正后系统开环波特图Figure 5. Bode diagram of open-loop of corrected system

图6 校正后系统输出阶跃响应Figure 6. Output step response of the system after correction

3.3 优化后输出电流对闭环稳定性的影响

假定优化后的电路参数不变，当输出电流Io从额定的10 A增加到24 A时，如表3所示，kmax的值由正变负。如图7所示，系统的相频曲线上重现严重的相位滞后。如图8所示，由系统的零极点图上可以看出复零点从左半平面移动到了右半平面。如图9所示，系统的阶跃响应相比输出电流Io增加前，过冲幅度增大和振荡次数变多，控制系统闭环不稳定。

图7 系统输出过流前后的系统频率特性Figure 7. System frequency characteristics before and after system output overcurrent

图8 系统输出过流前后的零极点的位置Figure 8.Position of zero-pole before and after system output over current

图9 系统输出过流前后的阶跃响应Figure 9. Step response of the system before and after output over current

表3 kmax的值与输出电流Io的变化关系Table 3. The relationship between the value of kmax and the change of output current Io

当输出电流Io从24 A减小至10 A的过程中，如表3所示，kmax的值逐渐由负变正，位于右半平面的零点移动到了左半平面，环路增益的相位滞后减小到了180°以内，输出阶跃响应振荡次数、超调量减小，闭环不稳定现象消失。实验数据表明，要使得系统闭环稳定，必须限制输出电流的大小，使变换器在运行过程中kmax的值始终为正。

此外，表3的实验数据表明文中提出的优化设计方法能够使输出电流的大小与系统闭环稳定所允许的最大输出电流之间留有足够的设计余量，即使在运行过程中输出电流偏离额定值的2倍时，仍然能够维持闭环系统的稳定性。只有负载在极端情况下(例如输出端发生严重的过流或者短路故障)，才会导致系统闭环不稳定。如果系统设计有负载过流保护模块，将保护阈值设定为kmax的临界值所对应的电流值，则可避免该情况发生。

4 结束语

相比于基于智能算法的参数优化方法[18]，本文的参数优化设计方法的优点是操作流程较为简单，在设计过程中较容易把握系统的频率特性以及零极点位置变化的趋势，可避免零极点落入右半平面，改善了系统的频率响应及频率域相对稳定性指标，使设计者采用简单的控制策略即可实现对四阶变换器的控制，并且在负载电流超过额定值的情况下也能够发挥其最大的优化作用，确保系统闭环稳定。

本文的方法缺点在于对系统环节的划分时，频率特性参数的求解采用了近似计算，无法达到精确的解析解。使用本文方法在某些情况下对幅频特性曲线的优化并不能达到最佳效果，致使输出电压的阶跃响应存在一定量的高频峰值响应，但仍然能够保证在给系统设计控制器时，把开环相频特性的最大相位滞后减小到180°以内，消除系统闭环不稳定的风险。