基于改进小波阈值去噪和CEEMDAN-HT融合的谐波检测技术

2023-01-03王玉梅

电子科技 2023年1期

王玉梅，郑义

(河南理工大学电气工程与自动化学院，河南焦作 454000)

随着电网中分布式新能源渗透率逐渐提高，大量非线性和冲击性的负荷被投入使用，导致电网电压与电流发生畸变，谐波含量上升。谐波治理过程中，电网环境噪声使谐波信号极值分布及大小呈现随机性变化[1-2]，谐波信号易出现间歇情况。经验模态分解(Empirical Mode Decomposition，EMD)检测染噪谐波易导致模态混叠和端点效应等问题[3]。文献[4]发现高斯白噪声具有零均值特性。文献[5～7]提出将高斯白噪声加入原始信号弥补信号缺失尺度的改进算法，例如集总经验模态分解(Ensemble Empirical Mode Decomposition， EEMD)、互补集总经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)，在一定程度上克服了模态混叠。但是噪声的随机性使每次EMD分解得到的固有模态函数(Intrinsic Mode Function，IMF)数量不同，平均化处理时难以对齐。文献[8]将自适应噪声的完全集合经验模态分解(Complete Ensemble Empirical Mode Decomposition of Adaptive Noise， CEEMDAN)应用于谐波检测，有效克服了模态混叠和难以平均化的问题，但该方法忽略了噪声引起迭代次数增加的问题。

小波变换良好的自适应性符合低频信号变换缓慢和高频信号变化迅速的特点，能较好地保留有效信号中的突变和尖峰部分[9]。此外，软、硬阈值因去噪计算量小、去噪效果好的优势而得到广泛应用，但阈值的选取和阈值函数的构造将直接影响去噪效果。文献[10] 在综合软硬阈值函数和Garrote阈值函数的基础上，通过引入一个0～1的可调参数来克服原有的偏差性和不连续问题，但该算法整体计算量较大。文献[11～13]以不同的可调参数优化阈值函数，去噪效果有所改善，但阈值无法根据信号中噪声分布自适应调节。

为更好地抑制噪声影响，有效保留谐波信号特征，保证CEEMDAN检测准确性和实时性，本文提出基于改进阈值函数和自适应修正阈值的小波去噪与CEEMDAN-HT融合的检测新方法，克服了CEEMDAN带噪分解存在的模态混叠现象，同时解决了希尔伯特变换(Hilbert Transform，HT)检测出现负频率的情况。研究结果表明，所提出的新方法能够在噪声环境下对电网的稳、暂态谐波精确检测和识别。

1 改进小波阈值去噪

1.1 自适应修正阈值

传统阈值表达式如下

(1)

式中，噪声标准差σ[11]的作用是对信号整体中的噪声进行近似估计；N表示信号长度。传统阈值由信号长度决定，但随着分解层数增加，阈值是逐渐减小的，噪声则均匀分布在小波域，采用固定阈值会使某些小波分解层噪声去除过多，损失有效信息，因此需要建立分解层数与阈值的约束关系[14]

(2)

式中，λj表示每一层小波系数的阈值；j表示分解层数，当j越大时，λj越小。使用过程中，需运用一种基于峰和比的修正因子Tj对阈值进行修正[15]，首先定义第j层小波系数的峰和比如下

(3)

式中，PSRj表示第j层小波系数中有效信息与噪声信息的近似含量，其值越大代表该层有效信息越多，反之则相反。由峰和比引出修正因子，定义如下

(4)

式中，Lj为第j层小波系数的长度。将修正因子代入式(2)得到自适应修正阈值，如式(5)所示。

(5)

1.2 改进阈值函数

传统的小波阈值函数主要有两种：硬阈值函数和软阈值函数，其表达式分别为式(6)和式(7)。

(6)

(7)

利用式(6)对信号进行去噪，保留大于λ的小波系数，将小于λ的小波系数直接置零，从而实现去噪，但在λ处不连续，存在间断点。式(7)弥补了式(6)λ处不连续的缺点，但其收缩变换的性质导致去噪后与原信号存在恒定偏差[15]。为解决以上问题，对阈值函数进行改进，如式(8)所示。

(8)

改进的阈值函数中，合理选取τ值可使阈值函数同时具备软、硬阈值函数的特性，可实现软、硬阈值函数的平滑切换。改进阈值与软、硬阈值特性对比如图1所示。

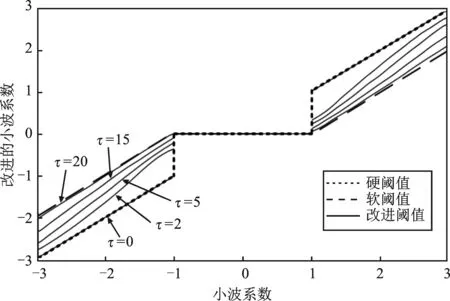
图1 阈值函数特性对比Figure 1. Characteristic comparison of threshold function

1.3 去噪效果分析

为了验证基于自适应修正阈值的改进小波阈值去噪效果，本文选取由基波、3次谐波和噪声信号组成的染噪电压信号，具体为

(9)

式中，e(t)表示强度为0.2的高斯白噪声，信号信噪比(Signal-to-Noise Ratio，SNR)为19.87 dB。通常情况下，db4小波对非平稳信号更加灵敏，因此在此试验中运用db4小波为小波基，分解层数为5层，信号时长0.5 s。

本文选取传统软、硬阈值去噪、无修正因子小波阈值去噪及本文所提的方法进行对比，并运用信噪比和均方误差(Root Mean Square Error，RMSE)[15]两种指标量化去噪效果，所得数据均为进行50次试验所求得的平均值，数据如表1所示。

表1 降噪指标结果Table 1. Noise reduction index results

由表1可以看出，相较于传统小波阈值和无修正因子去噪，基于自适应修正阈值的改进小波阈值去噪对信号SNR有显著提高，均方误差也有不小程度的减小。图2中，去噪信号波形比较平滑，信息损失小，但在个别点上略有差异，可见自适应修正阈值的改进小波阈值去噪效果较为理想。

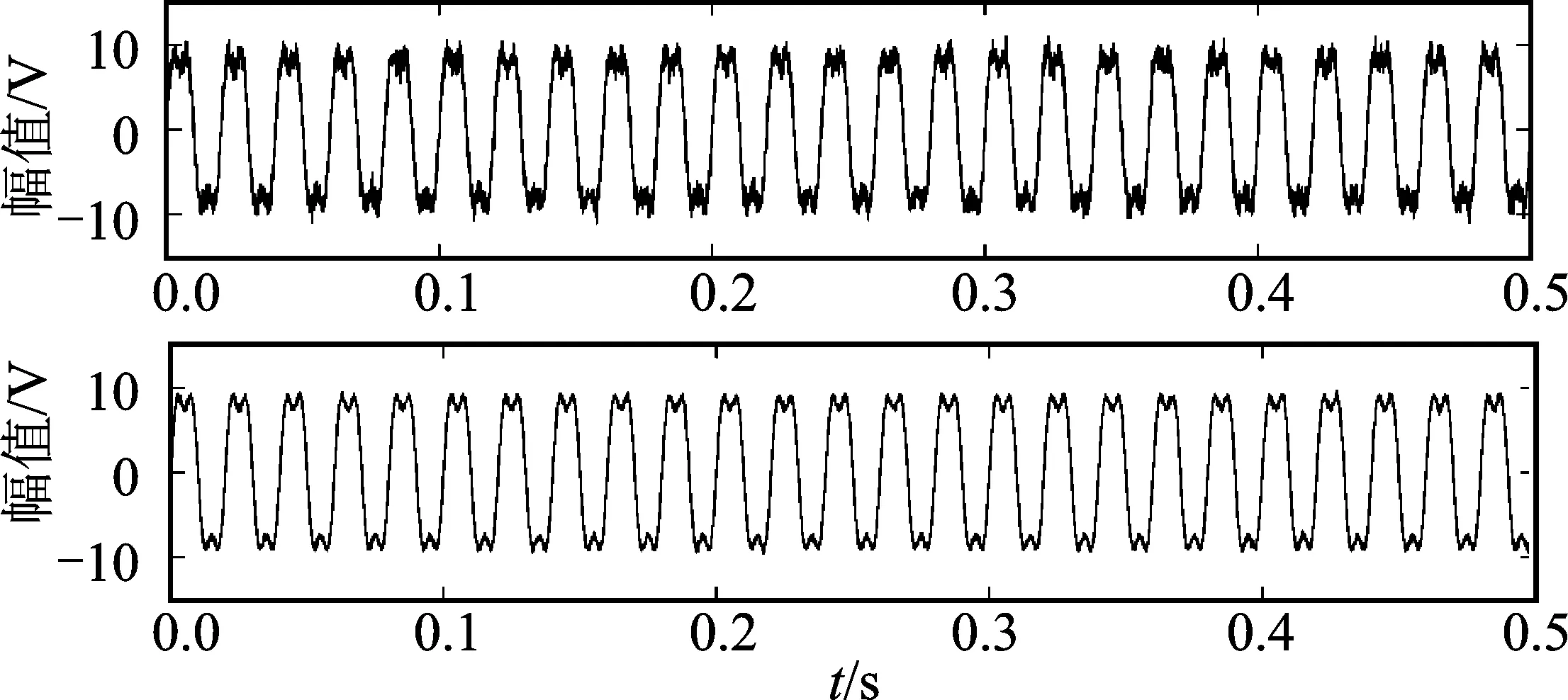
图2 改进小波阈值去噪Figure 2. Improved wavelet threshold denoising

2 CEEMDAN算法

CEEMDAN算法的具体步骤如下：

(10)

(11)

步骤2将EMD分解所得到的白噪声分量(-1)aη1s1(mi(t))添加到最终第1阶剩余分量r1(t)，构成新信号如下

w1(t)=r1(t)+(-1)aη1s1(mi(t))

(12)

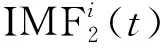
(13)

(14)

步骤3继续分解，将第k阶噪声分量(-1)aηksk(mi(t))加入到rk(t)构成第k个信号。

wk(t)=rk(t)+(-1)aηksk(mi(t))

(15)

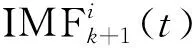
(16)

(17)

步骤4重复步骤3，持续分解直到rk(t)所含极值点小于2或表现单调性，最终得到k个IMF分量，并得到最终残差res(t)，如式(18)所示。

(18)

3 改进小波阈值去噪和CEEMDAN-HT融合的算法

3.1 算法融合思路

CEEMDAN作为处理非线性、非平稳信号的一种工具，相较于EMD有抑制端点效应[16-17]和模态混叠的能力。但在处理染噪谐波信号时，CEEMDAN分解迭代次数增加，计算量加大，并伴随模态混叠和噪声残留。此外Hilbert变换抗噪性不强，无法准确测出带噪IMFs的特征信息[18]。基于以上问题，运用小波阈值法良好的去噪性能，对染噪谐波信号进行预处理，能够有效提高CEEMDAN-HT的检测精度。传统小波阈值法存在阈值选取固定及阈值函数不连续和恒定偏差问题，本文通过阈值修正使阈值选取具备自适应性，利用可调参数τ实现软、硬阈值函数的平滑切换，保留了谐波信号的特征信息。CEEMDAN对预处理后的谐波信号分解，使迭代次数大幅降低，同时各IMF中几乎无混叠现象。两者的融合实现了优势互补，从而实现了对高次谐波、暂态谐波的准确检测。

3.2 融合算法的实现步骤

步骤1设谐波信号模型Z(t)，将高斯白噪声和定量的随机噪声加入信号中构成新信号C(t)，如下

(19)

式中，i=1，2，…，n；di为各分量幅值；fi=50 Hz，150 Hz，…；e(t)为噪声分量；

步骤2运用离散小波变换(Discrete Wavelet Transformation，DWT)对信号进行分解，通过修正因子Tj修正阈值；

步骤3改进阈值函数处理小波系数μj，k并重构信号，得到去噪谐波信号X(t)；

步骤4对X(t)进行CEEMDAN分解并运用相关度判据对IMFs进行判定；

步骤5将筛选后的IMFs进行Hilbert变换得到

(20)

式中，ψk为第k个Hilbert变换；ξ为时间，引出解析信号

(21)

瞬时幅频函数则如下所示。

(22)

(23)

4 仿真分析

4.1 稳态谐波仿真实验分析

本文分析了当风电系统存在时的光伏并网。光伏系统的随机性导致系统电压中产生3、5、7次谐波[19]，由此构建稳态谐波模型如下

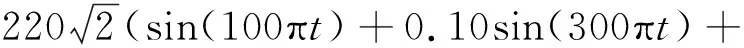
0.08sin(500πt)+0.05sin(700πt))

e1(t)=randn(1，12 800)；

e2(t)=awgn(Z(t)，20，′measured′)；

(24)

式中，e1(t)为服从正态分布的高斯白噪声；e2(t)是功率20 dB的高斯白噪声。在满足奈奎斯特采样定理的前提下，采样频率越高，时域内分辨率就越高，采集信号就越接近原信号。经实验验证得知采样频率为12.8 kHz即可较好地采集信号特征。本文信号模型均未经滤波器滤波，且经相位角测量，所设采样频率为未影响信号相位，因此本文不考虑延时和相位变化。通过R=corrcoef(x，imfi)函数去除虚假分量。

图3 染噪信号及去噪Figure 3. Noise signal and denoising

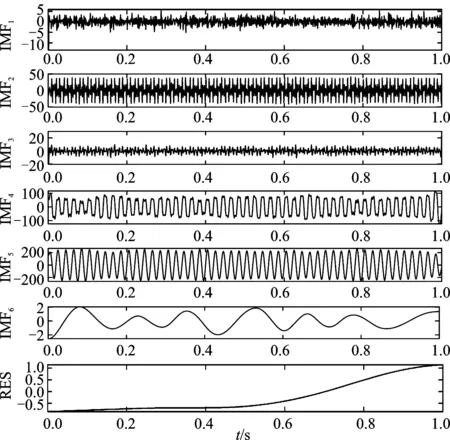
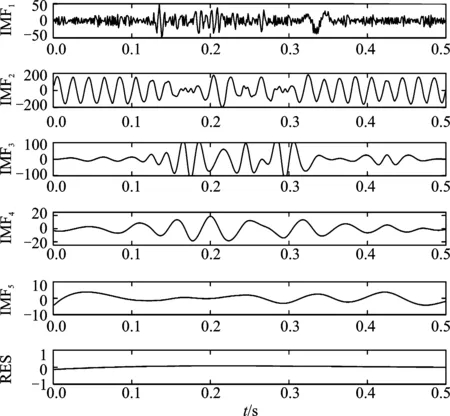
由图4(a)可知，IMF1为噪声信号，其余各阶IMF中都存在模态混叠现象和噪声残留，分解不完整。图4(b)中，由于CEEMDAN通过正负成对的白噪声在分解过程中相互抵消，减小了噪声的干扰。IMF1、IMF3主要特征为噪声，夹杂着少量谐波分量。IMF2、IMF4表现出谐波特征，但IMF2、IMF4存在明显的模态混叠。IMF5为基波分量，波形较为光滑，存在轻微模态混叠。IMF6是虚假分量可以忽略。图4(c)中，在去噪后克服了模态混叠和噪声影响，各次谐波分量可被准确分离出来，端点处出现轻微飞翼，IMF1～IMF4无论波形与幅值都近似350 Hz、250 Hz、150 Hz和基波分量，而IMF5～IMF8则波形单一。为判断图4(c)中IMFs是否为原信号分量，本文使用相关度判据对其判定，设定阈值为0.1，相关系数如表2所示。

(a)

(b)

(c)图4 EMD与CEEMDAN分解(a)EMD分解 (b)CEEMDAN分解(c)改进小波阈值去噪-CEEMDAN分解Figure 4. EMD and CEEMDAN decomposition(a)EMD decomposition (b)CEEMDAN decomposition(c)Improved wavelet threshold denoising-CEEMDAN decomposition

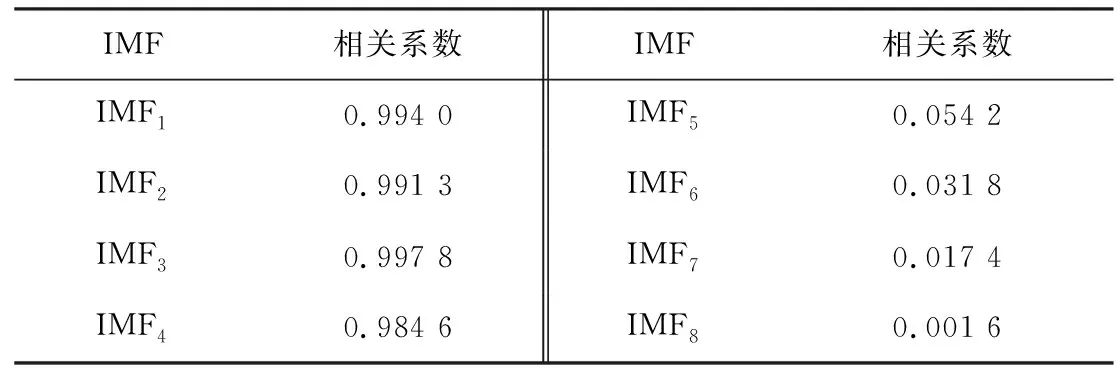
表2 图4(c)中IMFs与原信号的相关系数Table 2.Correlation coefficient between IMFs and original signal in figure 4(c)

由表2可知，IMF5～IMF8分量与原信号相关系数小于0.1，故可认定其为虚假分量并进行剔除，最终得到IMF1～IMF4及残余分量RES。为确定筛选后IMFs的谐波特征，现对IMF1～IMF4进行Hilbert变换，获取准确的幅值-频率信息，如图5所示。

图5 IMF分量Hilbert变换Figure 5. Hilbert transformation of IMF component

由图5可知，经去噪、分解及相关度判定后，各IMFs分别代表各次谐波分量，基波与3、5、7次谐波分量被准确分离。观察图5可知，各IMFs的幅频信息存在细微波动，但整体平稳，证明边际谱能准确反映IMF1～IMF4的瞬时幅频信息。具体数据对比如表3、表4所示。表中“—”表示无法检测，后同。

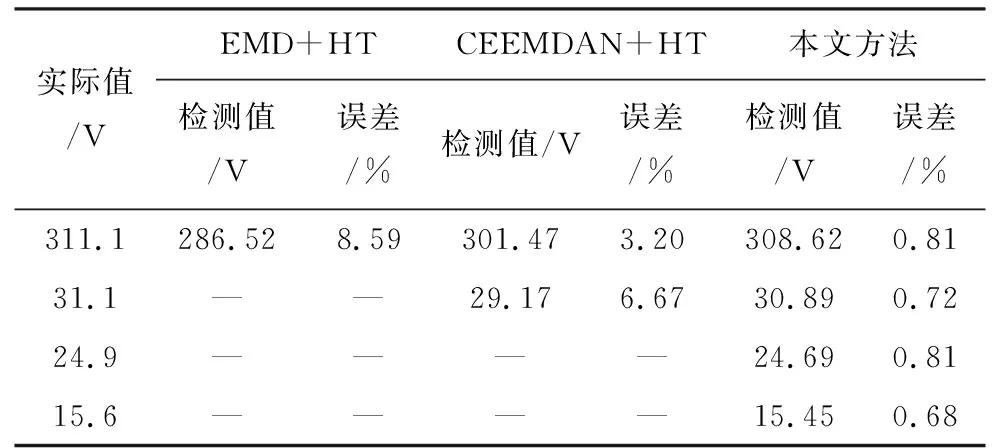
表3 谐波检测瞬时幅值信息Table 3. Instantaneous amplitude information of harmonic detection

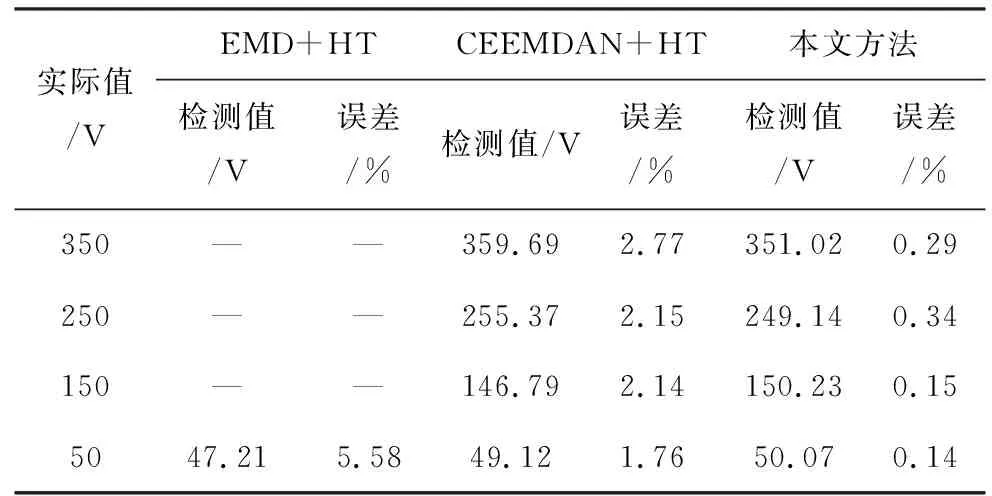
表4 谐波检测瞬时频率信息Table 4. Instantaneous frequency information of harmonic detection

根据表3和表4可以看出，EMD-HT方法与CEEMDAN-HT方法存在严重的模态混叠，其瞬时幅值-频率检测平均误差分别为4.99%和2.21%。本文方法不仅分解准确，而且瞬时幅值-频率检测平均误差分别为0.76%和0.23%，说明本文方法性能更优。

4.2 暂态谐波仿真实验分析

在实际电力系统中，谐波虽属于稳态扰动，但对于暂态谐波的检测着重于检测扰动的起止时刻。本文对所提出的方法对于暂态谐波的适用性进行了验证，构造暂态谐波信号如下

C2(t)=150sin(100πt)+27β(t)sin(300πt)+

e1(t)+e2(t)

(25)

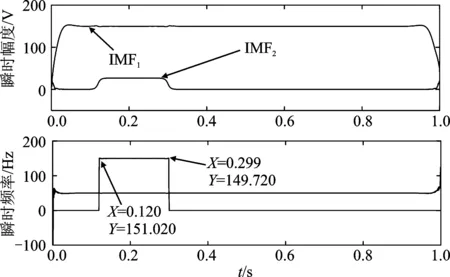
式中，β(t)为谐波影响因数，当0.12 s≤t≤0.3 s时，β(t)=1，在t<0.12 s及0.3 s

由图6可知，将染噪暂态谐波信号去噪后，波形毛刺明显减少，具有良好的平滑性。图7(a)中EMD存在严重模态混叠，无法辨识基波与暂态扰动。图7(b)仅运用CEEMDAN对染噪暂态信号分解，IMF1为噪声信号，其余模态显示并未将基波完整提取出来，整体效果不理想。图7(c)将染噪暂态信号去噪后进行分解，其中IMF1为3次谐波扰动，除个别端点处存在较大的幅值变化，整体波形完整平滑，IMF2为基波分量，IMF3～IMF5经相关度判据判定为虚假分量。对IMF1、IMF2进行Hilbert变换确定暂态扰动起止位置，结果如图8所示。

图6 暂态模拟信号去噪Figure 6. Denoising of transient analog signal

(a)

(b)

(c)图7 暂态信号EMD和CEEMDAN分解 (a)EMD分解 (b)CEEMDAN分解 (c)改进小波阈值去噪-CEEMDAN分解Figure 7. EMD and CEEMDAN decomposition of transient signal(a)EMD decomposition (b)CEEMDAN decomposition (c)Improved wavelet threshold denoising-CEEMDAN decomposition

图8 暂态扰动分量Hilbert变换Figure 8. Hilbert Transformation of transient disturbance component

图8(a)中IMFs的幅值检测与基波分量显示3次谐波扰动有极小的误差，基波幅值误差范围在0.20%～1.71%之间，三次谐波扰动幅值误差范围在0.11%～1.97%。图8(b)则表明，基波分量频率误差范围在0.92%～1.56%，150 Hz暂态扰动分量频率误差范围在0.60%～1.98%。综合图8中数据判定暂态扰动开始时刻为0.120 s，终止时刻为0.299 s，即实现了对暂态谐波信号的准确定位。