低开关频率下永磁同步电机转矩预测控制

冀梦齐,肖 霆,刘念洲

应用研究

低开关频率下永磁同步电机转矩预测控制

冀梦齐,肖 霆,刘念洲

（船舶综合电力技术重点实验室，武汉 430064）

针对预测型直接转矩控制电机转速响应稳态误差较大的问题，本文提出了一种控制策略，通过构建永磁同步电机的转矩预测控制器代替传统预测型直接转矩控制使用的PI型控制器，有效地消除了预测型控制在低开关频率下产生的永磁同步电机转速响应的稳态误差。本文采用MATLAB/Simulink对所提出的控制方法进行仿真验证，仿真结果证明所提控制方式可以有效地消除传统预测控制在低开关频率下出现的稳态误差。

直接转矩控制 预测转矩控制

0 引言

永磁同步电机(permanent magnet synchronous motor，PMSM)凭借着其结构简单、传输效率高、功率密度高的优点，在工业领域有着广泛的应用[1]。永磁同步电机的直接转矩控制（direct torque control，DTC）方法结构简单且动态响应快，是一种成熟的高性能电机控制方式。

永磁同步电机在低开关频率控制时，由于采样频率低，直接转矩控制的控制量会超出滞环环宽，出现转矩脉动大、在启动区域响应迟缓的问题[2]。为了克服这些问题，文献[3-4]提出了预测型控制器。借助空间矢量调制，预测控制方法表现出了开关频率低、稳定，转矩响应快、脉动小的优点。然而这些预测性控制器在低开关频率下，由于采样频率低的原因，电机会出现随速度增加而增大的稳态误差和较大的超调量[5]。

本文提出了一种转矩预测控制策略，在定子磁链定向坐标系下进行定子磁链幅值和电磁转矩的解耦控制，去除了传统预测控制在转速环使用的PI控制器，有效地消除了传统预测控制在低开关频率下转速响应的稳态误差。

1 永磁同步电机数学模型

本文中将转子磁场定向的坐标系称为dq坐标系，直轴为d轴，交轴为q轴；定子磁场定向下的坐标系称为xy坐标系，直轴为x轴，交轴为y轴；静止坐标系称为αβ坐标系。

永磁同步电机在dq坐标系下的数学模型如下：

(1)

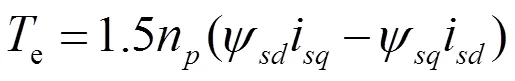
根据（6）式可从dq坐标系下的定子磁链获得αβ坐标系下的定子磁链，如下

在αβ坐标系下可求得定子磁链空间矢量的幅值和角度，如公式（7）（8）所示

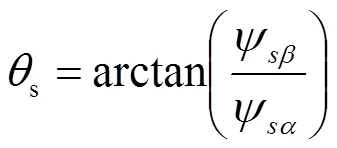
定义定子磁链与转子磁链的夹角为负载角，如公式（9）所示

通过坐标变换我们可以得到定子磁场定向下的定子电压方程，如下式所示

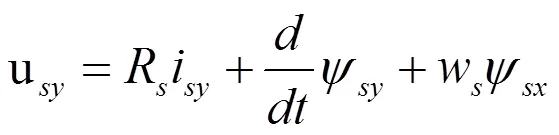
由于xy坐标系基于定子磁链定向，上式中

由公式（10）-（14）可总结出定子电压方程为

2 转矩预测控制

对（15）-（16）使用前向欧拉公式，得到定子电压离散方程

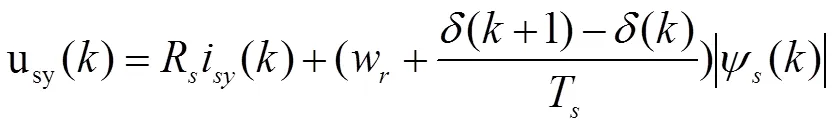
由公式（18）-（19）可知，由下个控制时刻磁链幅值与负载角的参考值可以推算出这个控制时刻应该给SVM模块的电压参考值，如下式

电磁转矩可以由定子磁链幅值和负载角表示如下[6]：

永磁同步电机转子磁链是恒定的，电磁转矩只受定子磁链幅值和负载角的影响。对公式（22）两边对时间求导得

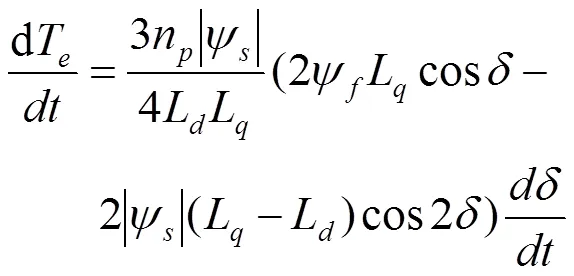
对公式（23）使用前向欧拉公式进行离散可得电磁转矩与负载角有如下关系

其中

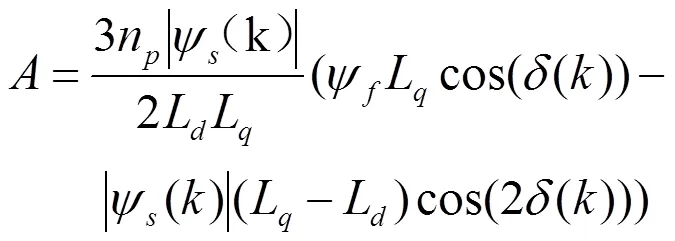
电磁转矩与转速的关系为

采用前向欧拉公式对式（26）进行离散得

模型预测控制需要对未来系统的状态进行预测，我们记未来p个控制周期内预测的系统状态为：

P称为预测时域，括号中k+1|k表示当前k时刻预测k+1时刻的系统状态。

由（27）-（29）可得

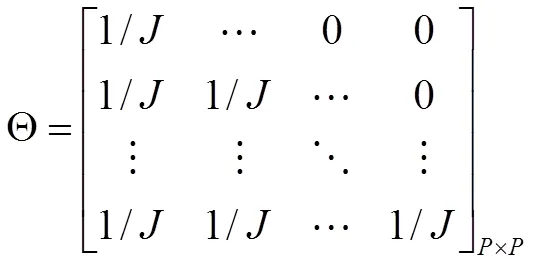
为了使得预测时域内的转速向量与参考给定转速越接近越好，用预测转速向量与参考给定向量的累计误差定义一个简单的优化目标函数：

为使控制量动作不会太大，优化目标函数添加一相对控制量的约束

因此，该优化问题可以描述如下：

根据公式（26）可得电磁转矩给定参考值为：

3 仿真验证

图1 转矩预测控制框图

为了验证上述推导和结论的正确性，本文对所提出的转矩预测控制进行了仿真验证。其控制框图如图1所示：

电机参数如表一所示：

本文在matlab/simulink中对传统预测控制和所提出的预测控制效果进行了对比仿真实验，仿真中开关频率为500 Hz，数字控制的采样频率为500 Hz，仿真时长为0.2 s。仿真实验中电机在给定参考转速为额定转速(50 rad/s)情况下控制启动，启动转矩限制在0.8 N.m，在运行到0.1 s时加入额定负载（0.25 N.m）。从实验结果图2可以看出，传统预测控制在低开关频率低采样频率下会出现稳态误差不为零的情况，由图3可以看出所提转矩预测控制策略可以有效地消除低开关频率下的稳态误差，并且不会对控制引入其它问题。

表1 电机参数

图2 传统预测控制下电机输出波形图

图3 所提出控制策略下电机输出波形图

4 结论

本文提出了一种针对永磁同步电机的转矩预测控制策略，解决了低开关频率下预测性控制器电机转速响应稳态误差较大的问题。所提控制策略动态响应快，转矩脉动小，但因为要进行优化求解，比传统预测控制的计算量大。本文在仿真使用的给定参考磁链幅值恒定，因此在低转矩负载时也会存在较大的定子电流，存在较大的损耗。损耗优化问题可作后续的研究内容。

[1] 王莉娜, 朱鸿悦, 杨宗军. 永磁同步电动机调速系统PI控制器参数整定方法[J]. 电工技术学报, 2014, 29(5): 104-117.

[2] Habetler T G, Divan D M. Control strategies for direct torque control using discrete pulse modulation[C]//Conference Record of the IEEE Industry Applications Society Annual Meeting. San Diego, CA, USA: IEEE, 1989: 514-522.

[3] Yan H Z, Ye Y Q. Improved deadbeat direct torque control of interior permanent magnet synchronous motor with flux linkage reference correction[C]//2017 IEEE International Electric Machines and Drives Conference (IEMDC). Miami, FL, USA: IEEE, 2017: 1-6.

[4] Wang Y L, Wang X C, Xie W, et al. Deadbeat model-predictive torque control with discrete space-vector modulation for PMSM drives[J]. IEEE Trans Ind Electron, 2017, 64(5): 3537-3547.

[5] Lee J H, Kim C G, Youn M J. A dead-beat type digital controller for the direct torque control of an induction motor[J]. IEEE Trans Power Electron, 2002, 17(5): 739-746.

[6] Lin X G, Huang W X, Jiang W, et al. Deadbeat direct torque and flux control for permanent magnet synchronous motor based on stator flux oriented[J]. IEEE Trans Power Electron, 2020, 35(5): 5078-5092.

Torque predictive control of permanent magnet synchronous motors at low switching frequency

Ji Mengqi, Xiao Ting, Liu Nianzhou

(Key Laboratory of Ship Integrated Power Technology, Wuhan 430064, China)

TM341

A

1003-4862（2022）12-0061-04

2022-05-29

冀梦齐（1997-），男，硕士。研究方向：电力电子与电力传动。E-mail: 1355424460@qq.com