一种电力电子变换器固有频率仿真提取方法

陈宇航，金 翔，李 锐

应用研究

一种电力电子变换器固有频率仿真提取方法

陈宇航1，金 翔2，李 锐2

（1. 海装驻葫芦岛地区军事代表室，葫芦岛 125000；2. 武汉第二船舶设计研究所，武汉 430074）

为了简化电力电子变换器固有频率的仿真过程，减少建模工作量，并提高其固有频率提取的精度，本文首先针对电力电子变换器的仿真模型建立过程，提出了一种新的模型简化方法，并对仿真后得到的固有频率，提出了一种根据模态参与因子进行固有频率提取的方法。最后对比了固有频率的仿真和实验结果，两者的误差能控制在10%以内，验证了新方法的有效性。

电力电子变换器 固有频率 模态参与因子

0 引言

电力电子变换器在舰船电力推进系统、供配电系统中得到了广泛应用。电力电子变换器中功率器件的开关动作，会产生以PWM开关频次为主的高频谐波电流，这些电流又会产生以PWM开关频次为主的高频振动。与此同时，电力电子变换器也会受到外界振动的影响。这些振动激励的频率与电力电子变换器固有频率一致时将会导致“共振现象”。

“共振现象”长期的作用，会对电力电子变换器的结构造成应力及疲劳破坏，从而导致电力电子变换器内部精密器件的焊点断裂，使电力电子变换器失效[1]。因此，为了避免因“共振现象”导致电力电子变换器失效的问题，在外界振动不可测的前提下，需要对电力电子变换器开关动作频次进行设计，使以PWM开关频次为主的高频振动避开电力电子变换器的共振频率，而这样做的基础是能够获得电力电子变换器的各阶固有频率。

在现有技术中，传统的模态仿真方法大多通过对连接部位特殊建模和参数修正方法，来获得和模态试验相近的固有频率[2-5]。这种方式对简单器件的固有频率提取效果良好，但仍存在以下几个问题：

1）对于结构复杂度高的器件仿真建模时间过长；

2）当研究对象与其他器件连接时，若其振动关联度不大，可能会得到非研究对象的固有频率，导致研究对象固有频率提取异常；

3）复杂器件仿真会得到频谱分布较密集的固有频率，得到的各阶固有频率对振动的贡献度并不相同，需要通过后续的处理筛选出对振动影响较大的固有频率。

本文针对上述问题，首先对电力电子变换器进行基础拓扑结构建模，通过对比各结构的振动幅度，进行模型的简化，之后对仿真得到的固有频率，通过对比模态参与因子的大小，提取出合适的固有频率，并与实验结果进行对比。

1 模态基础理论分析

在模态空间的概念中，固有频率是指结构受到外界瞬态激励时，产生振动时的特定频率。固有频率是结构的特有属性，不随外界激励变化而变化。固有频率值可以通过求解运动方程组来得到。对于无阻尼单自由度系统，其示意图如图1所示，若是扩展到多自由度系统，可以得到特征运动方程组如式（1）所示[6]。

图1 单自由度无阻尼系统示意图

由于特征模态总是可以叠加的，因此可以得到两个正交模态，即结构受到多频率的激励从而产生振动时，各阶模态只会在其各自的振型上线性叠加，故可以单独考虑不同模态在不同结构上的振动效应，即在两个结构振动关联性较弱时，可以视为两个单独的振动系统。

2 电力电子变换器的模型简化

本文所用方法的演示对象为实验室所用的隔离型双有源桥变换器（Dual Active Bridge，DAB）控制板，其实物如图2所示。

图2 DAB控制板实物图

控制板整体分为五层，从上到下分别为：复杂可编程逻辑芯片（Complex Programmable Logic Device，CPLD）板、采样板、母排、绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor，IGBT）和散热器。同时背面有两块驱动板连接在散热器上，其中，上三层结构、驱动板与其他层结构之间的连接方式为固定杆和固定点连接，下两层结构之间则通过紧密贴合的方式固定，基于振动的传递原理，可以分析得出下两层结构之间的振动传递比其他层更大。

在Solidworks软件中，对DAB控制板进行基本拓扑结构建模，如图3所示，其中因为散热板空隙较多，进行了完全切除处理。

图3 DAB控制板基础拓扑结构模型

之后将模型导入COMSOL仿真软件中，进行模态仿真，设置的材料参数如表1所示，设定各层电路板为电路板材料，IGBT为芯片材料，散热器、母排及连接杆为钢材料。

仿真得到的2 kHz以下的固有频率曲线如图4所示。

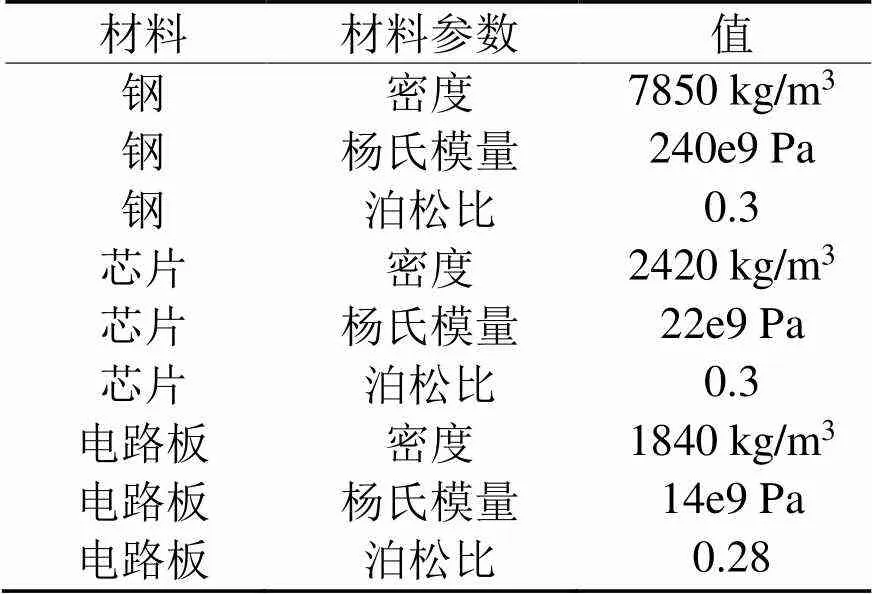
表1 仿真材料参数

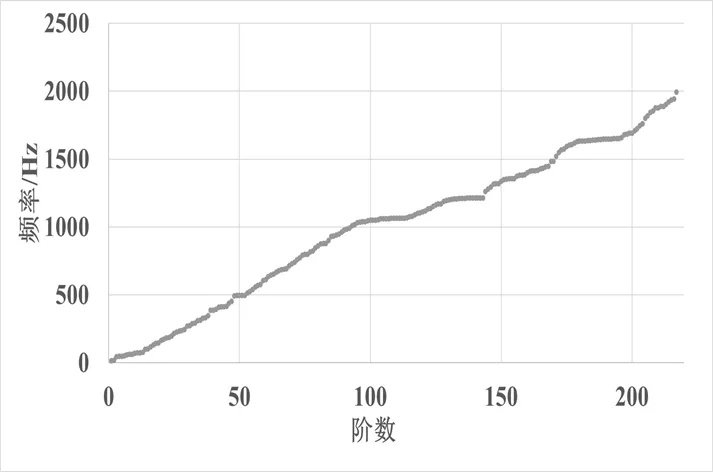
图4 DAB控制板基础拓扑结构模型仿真固有频率曲线

可以从图中看出，固有频率分布十分密集，平均每阶固有频率相差10 Hz左右。与表2中得到的实验固有频率比较可知，两者结果差距过大。

表2 实验固有频率

故这里对各层结构的振型再次分析，如图5所示。

图5 DAB控制板基础拓扑结构模型模态仿真振型及位移最大值示意图

通过现有软件计算不同模态振型中各部分的位移相对量大小（即归一化后的模态向量模），分别取研究主体（IGBT及散热板）及其他连接部位（CPLD板、采样板、母排）的位移相对量最大值，对比最大位移相对量的大小。若两者相差三个数量级以上，即不符合预设关联条件，则可认为两者之间的振动相关性很小，可互相独立分析。若两者相差三个数量级以内，则认为其振动相关性较大，需将两者共同建模。在图5中，其他各层结构与研究主体IGBT及散热板的位移相对量最大值相差都在三个数量级以上，因此，可以将对IGBT和散热板振动基本无影响的其他结构层忽略，单独研究IGBT和与其紧密贴合连接的散热器的模态。

从而将其他层的结构去除，进行重新建模，如图6所示。

图6 DAB控制板简化模型

进行模态仿真后得出分布在1400 Hz附近的30个固有频率，且各阶固有频率的振型都能反应在整体上，如图7所示，故基本的建模完成。

图7 DAB控制板简化模型模态仿真结果

之后进行精细化建模如图8所示。其中IGBT依照厂商的数据手册确定其结构及尺寸，主体部分由于内部结构紧密而进行一体化建模，对于四角螺栓连接孔由于实际有螺栓固定，因此采取填充处理。对于散热板，由于其镂空结构对质量刚度空间分布影响较大，作真实建模。

图8 精细建模DAB控制板简化模型

重复之前的仿真过程，得出的1400 Hz（预设频率）附近的30个固有频率如图9所示。

3 固有频率的提取方法

对于上一章所得到的仿真固有频率，可以看出，其分布还是较为密集，平均每阶固有频率相差25 Hz左右，需要对数据再进行分析处理。这里利用模态参与因子进行固有频率提取。

图9 精细建模DAB控制板简化模型模态仿真结果

模态参与因子是各激励自由度对各阶模态激励有效性的一种量度，是一个相对量，若同激励下模态其值越大，代表该模态对激励的动态响应的贡献越大，即在相同幅值的外界激励下，该阶固有频率处引起的振动幅值相对更大。模态参与因子的计算表达式如下所示：

这里的模态参与因子最大值为3.19E-11，取其1/3值作为判断阈值，即取参与因子大于1.06E-11的固有频率作为对激励响应有效的固有频率。图中有四处的参与因子符合条件，对于相邻固有频率取其平均值。与实验固有频率值进行比较，计算两者的误差，如表4所示。

表3 仿真与实验固有频率误差

可以看出，两者的误差都在10%以内，且除了第二阶，其他阶的误差都在1%附近，说明仿真与实验结果能非常准确地对应上，此方法效果显著。

4 总结

本文针对电力电子变换器，首先提出了一种根据各层结构振型中的振动幅度来进行模型简化的方法，能大大减少其他结构对目标固有频率仿真的干扰，之后利用模态参与因子对仿真固有频率进行提取，可以极大减少仿真与实验的误差。将两种方法结合后，可以提高电力电子变换器的固有频率仿真效率和准确性。

[1] 杨飞兵. 电子设备动力学分析及其振动控制[D]. 西安: 西安电子科技大学, 2012.

[2] Pitarresi J M, Caletka D V, Caldwell R, et al. The “smeared” property technique for the FE vibration analysis of printed circuit cards[J]. J Electron Packag, 1991, 113(3): 250-257.

[3] Pitarresi J M, Primavera A A. Comparison of modeling techniques for the vibration analysis of printed circuit cards[J]. JElectron Packag, 1992, 114(4): 378-383.

[4] Amy R A, Aglietti G S, Richardson G. Simplified modelling of printed circuit boards for spacecraft applications[J]. Acta Astronaut, 2009, 65(1/2): 192-201.

[5] Amy R A, Aglietti G S, Richardson G. Sensitivity analysis of simplified Printed Circuit Board finite element models[J]. Microelectron Reliab, 2009, 49(7): 791-799.

[6] 罗圣和. 印制电路板组件的振动分析与控制[D]. 西安: 西安电子科技大学, 2012.

[7] 汪建. 电动汽车动力总成NVH的分析与优化[D]. 杭州: 杭州电子科技大学, 2022.

A simulation extraction method for natural frequency of power electronic converters

Chen Yuhang1, Jin Xiang2, Li Rui2

(1. The Navy Representative Office in Huludao, Huludao 125000, China; 2. Wuhan Second Ship Design and Research Institute, Wuhan 430074, China)

TM46

A

1003-4862（2022）12-0034-04

2022-09-07

陈宇航（1991-），男，工程师。研究方向：舰船电力系统。E-mail：chen_yh316@126.com