基于DGC-t-MSV模型的国际航运市场和国际贸易市场波动溢出效应
2023-01-03董善华汪健吴慧媚
董善华, 汪健, 吴慧媚
(宁波航运交易所航运大数据中心,浙江 宁波 315040)
0 引 言
市场溢出效应指一个市场的波动不仅对自身产生影响,也会对其他相关市场产生影响。当前,国际航运市场和国际贸易市场进入了“调整期”。国际贸易市场方面,自2020年4月开始,中国出口贸易额一路走高。国际集装箱航运市场方面:2020年7月美国航线运价首先开始上涨,其后所有航线运价飞涨;2020年第4季度,市场出现缺舱、缺箱现象;2021年3月底受苏伊士运河阻塞事件影响,市场开始第二波涨价,所有航线运价均达到历年最高。
从两个市场走势的对比看,出口贸易在2020年4月开始走强,但并没有立即带动航运市场恢复。从数据上看,航运市场出现的缺舱、缺箱现象似乎并没有减缓出口贸易的增长,出口运价高昂和出口需求旺盛成为现阶段两个市场的突出特点。这是一种非常态的市场表现,急需进行有效的应对。
因此,研究国际航运市场和国际贸易市场的波动溢出效应,一是为了明确两个市场当前以及未来一个时间段内的发展趋势,二是为了明确两个市场波动的交互影响。在当前市场条件下,应对举措的侧重点是稳外贸还是稳航运,亦或是两者交叉发力,使政策举措的出台快速达到预期效果,对于维护国际航运市场和国际贸易市场的稳定具有十分重要的现实意义。本文研究结果不仅能助力企业预判后市,为其经营决策提供参考,而且有助于当前国际航运市场走出困境,促进国际航运市场和国际贸易市场的高质量发展。
1 文献综述
国际航运市场和国际贸易市场的波动历来受到市场和学界的关注,尤其是在新冠肺炎疫情给全球经济带来巨大影响的背景下。例如:杨长春[1]认为国际物流在随着国际贸易发展的同时,也已成为影响和制约国际贸易进一步发展的重要因素。姜宝等[2]基于向量自回归(vector auto regression,VAR)模型的估计结果,运用脉冲响应函数和格兰杰因果关系检验进行实证分析,得出上海出口集装箱运价指数(Shanghai containerized freight index,SCFI)与出口贸易额存在负相关关系。王璐[3]应用灰色关联度分析法,得出国际干散货海运量与世界经济具有很高的关联度。刘鹏等[4]采用灰色关联度分析法,研究波罗的海干散货指数(Baltic dry index,BDI)与国内港航类上市公司股价的联动性得出,从长期看两者具有较高的相关性,且随着我国对外贸易在国民经济中的比重逐步增加,其相关性逐步上升。蒋春艳等[5]建立灰色关联度模型,分析了上海区域经济与国际航运中心的产业互动发展,结果表明区域经济发展与港口发展具有很强的关联度。王天姿等[6]运用ARMA(1,1)-GARCH(1,1)模型和事件研究法,发现中国进口干散货航运价格的波动随着中美贸易争端的升级而显著增强,且受负面冲击事件的影响比受正面冲击事件的影响大,持续时间更长。马敏等[7]运用VAR模型,得出中国干散货贸易量对BDI的影响有限,而BDI对中国干散货贸易量变动起到一定的预见作用,可以将BDI作为预测中国干散货贸易量变动趋势的一个参考指标。朱慧[8]通过典型相关分析法得出国际航运中心与国际金融中心呈典型相关关系,且为正向相关。YANG等[9]构建了基于混合互补的均衡模型,分析国际航运市场对国际铁矿石贸易的影响,得出航运市场可以略微抑制非预期的进口商预算的减少对铁矿石贸易量的负面影响,对于不同的出口商这种抑制效果因运费而异。XU等[10]通过研究全球班轮运输网络与各个国家间贸易的关联性发现,一个国家融入全球班轮运输网络的程度越大,参与国际贸易的机会就越多,它在全球班轮运输网络中的地位与其在国际贸易中的地位有关。姜宝等[11]采用DCC-GARCH模型和DY溢出指数模型实证分析出国际航运市场与我国钢铁市场间具有动态相关性,滞后一周的航运指数与钢铁股价指数存在显著的弱相关关系,两个市场之间具有微弱的波动溢出效应,其价格传导机制存在断层现象。孙司琦等[12]通过动态条件相关系数多元随机波动(dynamic conditional correlation - multiple stochastic volatility, DCC-MSV)模型得出:国际贸易市场和国际航运市场存在波动持续性强、集聚性明显的特征,两个市场之间存在负相关关系,总体相关性不高;两个市场之间的波动存在正的双向溢出效应,集装箱运价对贸易额的溢出效应较明显。
根据现有研究可知,对国际航运市场与国际贸易市场的关联性研究多基于回归模型,而研究两者波动溢出效应方面的文献还比较少。本文在现有研究的基础上,考虑数据序列尖峰厚尾的特性,并弥补DCC-MSV模型在波动溢出传递方面的缺陷,构建引入t分布的带格兰杰因果关系检验的DCC-MSV模型(记为DGC-t-MSV模型),研究国际航运市场与国际贸易市场的动态相关性和波动溢出效应,推动市场的平稳有序运行。
2 模型研究设计
2.1 数据的选取及预处理
选取2014年1月—2021年6月的海上丝绸之路指数之宁波出口集装箱运价指数(Ningbo containerized freight index,NCFI)数据和中国出口贸易总额(EXP)数据,其中,EXP数据由海关总署每月发布,NCFI数据由宁波航运交易所每周发布。NCFI通过计算和记录从宁波舟山港出发的21条国际航线的集装箱运价变动信息,客观反映国际集装箱班轮运输市场的运价走势。将NCFI转化为月度数据,与EXP数据的频率保持一致。分别取NCFI和EXP序列的对数差分值以消除时间序列的异方差,得到RNCFI和REXP序列。
上海港集装箱吞吐量位居全球第一,宁波舟山港集装箱吞吐量位居全球第三、中国第二,可以说以上海港和宁波舟山港为始发港的航线的集装箱运价均能代表中国出口集装箱航运市场情况。之所以选择NCFI,是因为从上海港和宁波舟山港出口的集装箱运价并无太大差别。以欧洲线为例,2021年8月,从上海港、宁波舟山港出口到鹿特丹港的集装箱运价均值分别为8 173和8 294美元/TEU。在市场影响力方面,2015年10月,作为习近平主席访英期间中英双方达成的重要成果之一,NCFI在波罗的海交易所官方网站正式发布,这是波罗的海交易所历史上首次发布其他机构的指数,标志着中国航运指数首次获得了国际市场的认可。
2.2 统计特征分析
RNCFI和REXP序列的波动(见图1和图2)显示,两个序列均表现出波动集聚性,RNCFI的波动集聚性更明显。
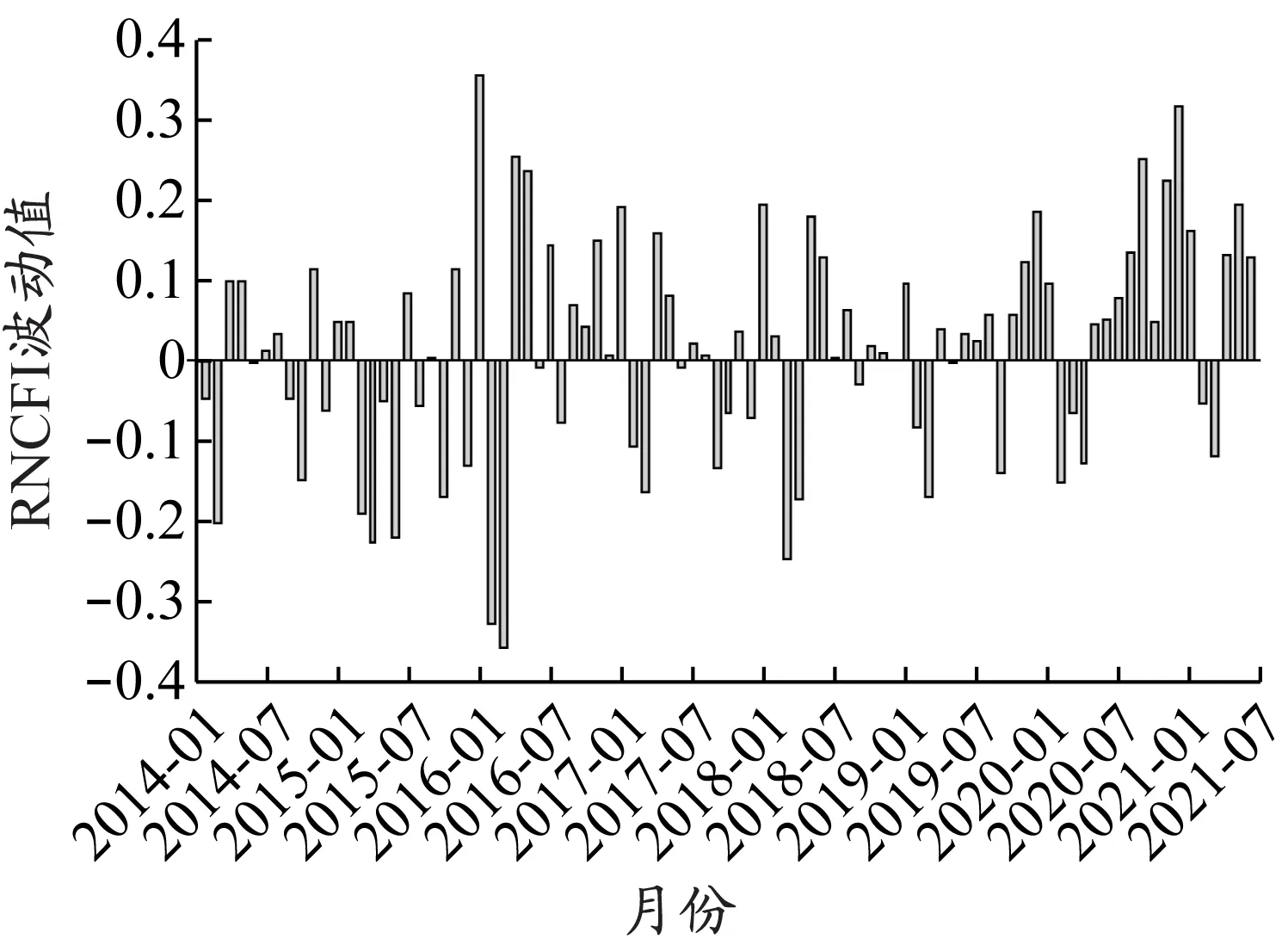
图1 RNCFI序列波动
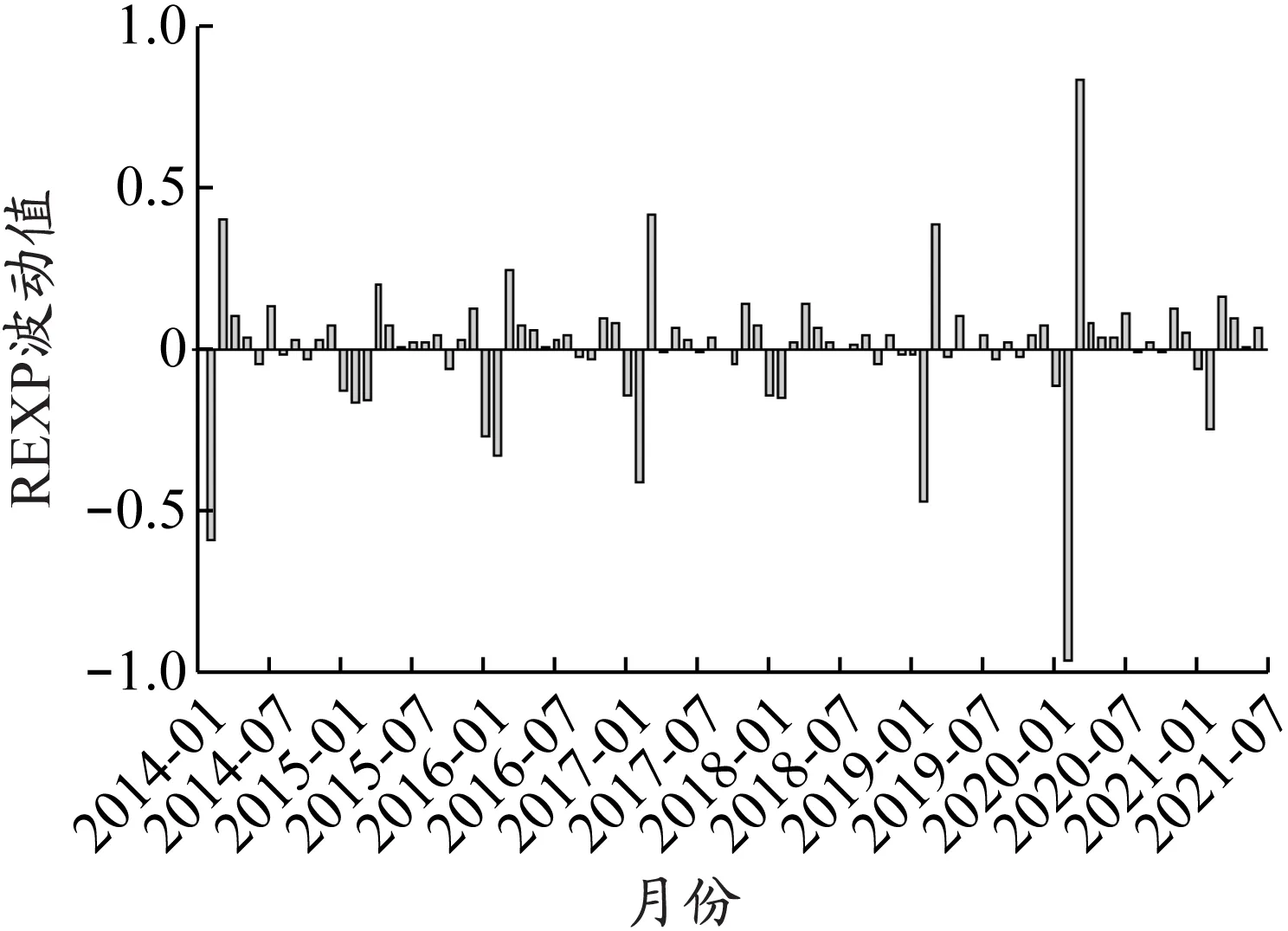
图2 REXP序列波动
RNCFI和REXP序列的描述性统计结果见表1:两个序列均值都接近0,RNCFI序列的标准差较小,说明NCFI的波动相对平稳;RNCFI序列和REXP序列的偏度都小于0,峰度均大于3,且J-B统计量都在1%显著性水平下显著,说明RNCFI和REXP序列均呈现显著的尖峰厚尾特征,两者均不服从标准正态分布。两个序列的ADF检验结果见表2:在1%显著性水平下,两个序列的P值均小于0.001,说明RNCFI序列和REXP序列均为平稳序列,可以直接进行参数估计。

表1 RNCFI和REXP序列的描述性统计
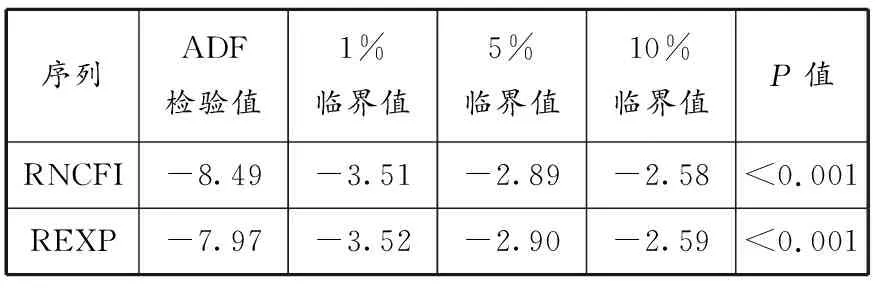
表2 RNCFI和REXP序列的ADF检验
2.3 模型构建
根据两个序列的统计特征,构造DGC-t-MSV模型,其中t分布用于刻画两个序列的尖峰厚尾特征,加入格兰杰因果关系检验用于追踪NCFI和EXP的波动溢出方向。模型基本形式如下:
ρt=(expqt-1)/(expqt+1)
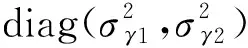
3 实证结果分析
WinBUGS软件是一款通过马尔科夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)方法分析复杂统计模型的软件,其基本原理就是通过Gibbs抽样算法和Metropolis 算法,从完全条件概率分布中抽样,从而生成马尔科夫链,通过迭代最终估计出模型参数[13]。使用WinBUGS软件对DGC-t-MSV模型进行建模,使用2条马尔科夫链共进行10万次迭代计算,舍弃前4万次预烧样本,得到参数估计结果。
3.1 模型收敛性判断
选取φ11、φ12、φ22和φ21的Brooks-Gelman-Rubin统计量图(图3)和后验密度图(图4)来判断模型的收敛性。如图3所示,Brooks-Gelman-Rubin统计量图的马尔科夫链趋近于1,且样本数据的总后验方差和内方差也趋向于1,说明基于Gibbs 抽样算法的MCMC方法可以较好地模拟模型的边缘后验分布[14]。如图4所示,后验密度图基本平滑,且只有一个尖峰,由此判断模型收敛。因此,构建的模型可以较好地分析NCFI与EXP之间的波动溢出关系。

图3 Brooks-Gelman-Rubin统计量图
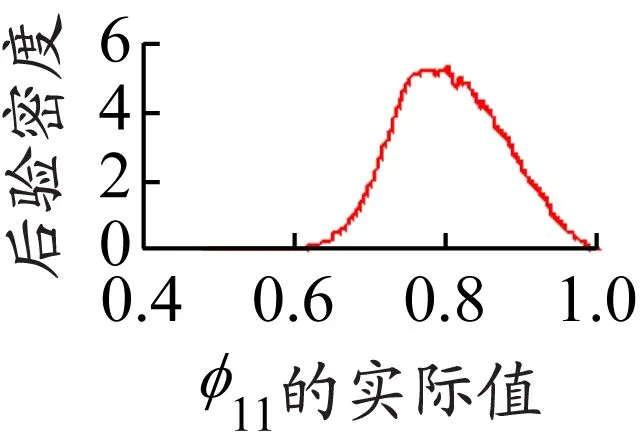
a) φ11

b) φ12
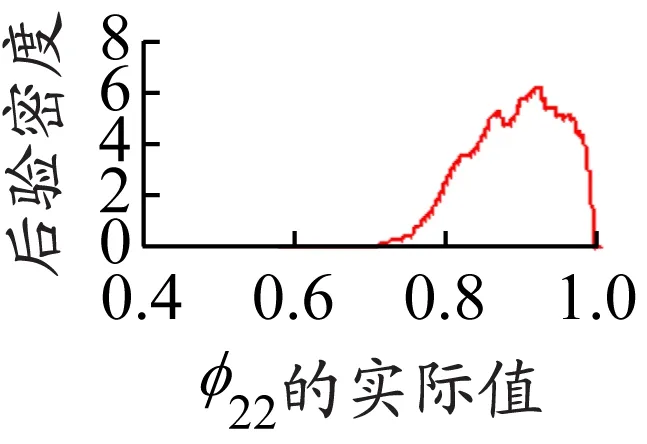
c) φ22
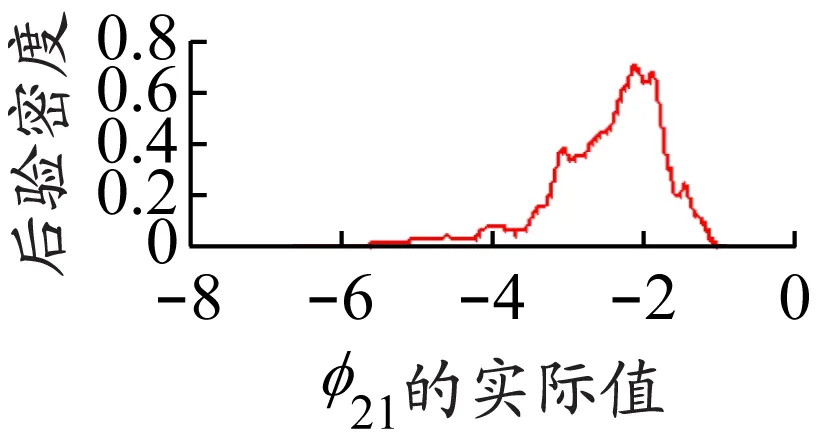
d) φ21
3.2 均值溢出效应分析
均值溢出效应主要反映NCFI与EXP之间的动态相关性和动态相关关系的持续性。由图5可知:两个序列的动态相关系数均值为0.13,总体呈现时变正相关性,虽然相关性不高,但从后期开始,动态相关系数的波动幅度开始提升。
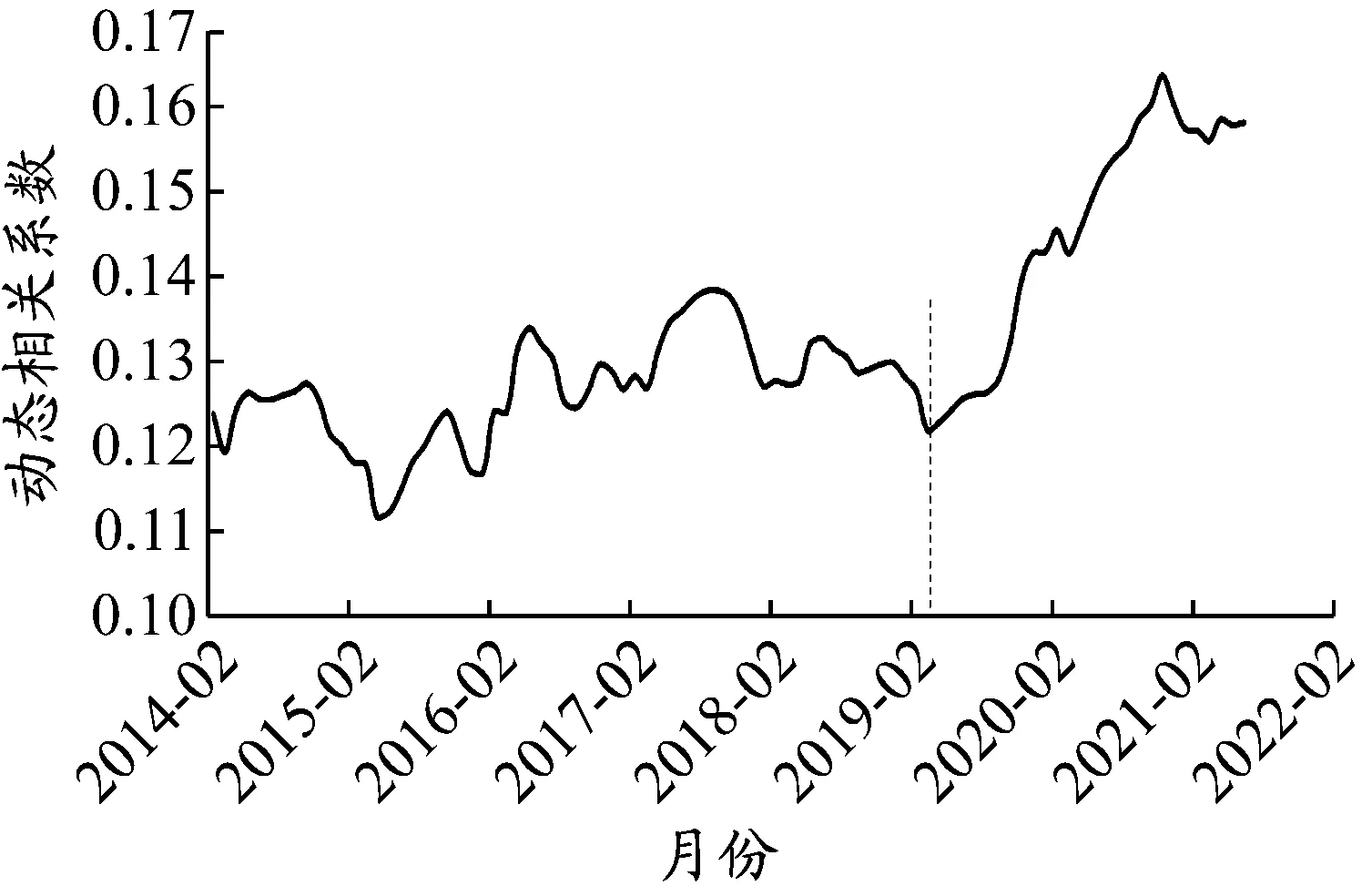
图5 RNCFI与REXP序列动态相关系数
由表3中2个序列的动态相关关系持续性系数Ψ的统计结果可知:Ψ的均值为0.84,接近1,说明两个序列自身波动持续性较强,受自身前期波动的影响较大,呈现出长期记忆特性,两个序列的波动集聚性都较显著。
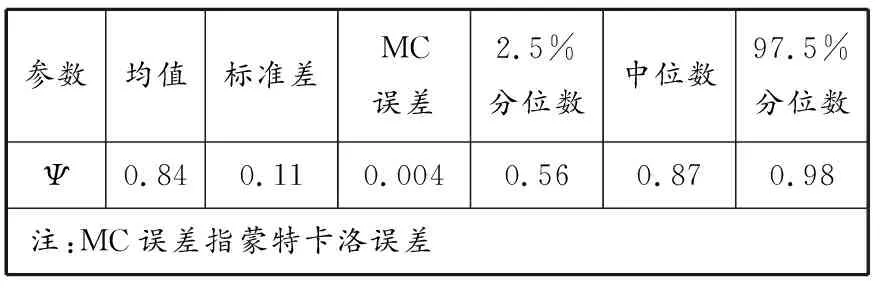
表3 RNCFI与REXP动态相关关系持续性系数Ψ的统计结果
3.3 波动溢出效应分析
波动溢出效应主要用于反映两个市场收益率之间信息传导的领先滞后关系、波动强度和波动传导方向[15],主要通过参数μ1、μ2、φ11、φ12、φ22和φ21进行判断。如表4所示:μ1的均值为-4.33,μ2的均值为-4.93,说明两个序列的波动强度相近;φ11和φ22的估计均值都大于0.8,说明NCFI和EXP的波动持续性都较强,均存在波动集聚性,且受自身前期波动的影响较大,具有长期记忆性;自由度d为6.09,显著异于0,说明这两个序列均具有尖峰厚尾特征,这与前面的统计分析结果一致。

表4 DGC-t-MSV模型参数估计结果
由表5可知:φ12的均值大于φ21的均值,说明NCFI对EXP的影响较大;在5%显著性水平下,φ12的t值为3.67,大于临界值1.96,φ21的t值为-3.04,明显拒绝原假设。由此可知,NCFI对EXP存在显著的单向格兰杰因果关系以及单向的波动溢出效应,NCFI是波动溢出的源头。
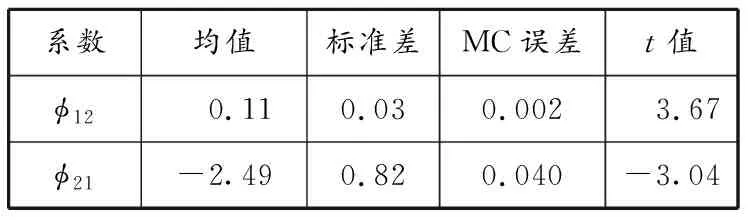
表5 波动溢出效应分析
4 总 结
本文构建了DGC-t-MSV模型,选取了宁波出口集装箱运价指数(NCFI)和中国出口贸易总额(EXP)两个数据序列,实证分析了两个市场之间的均值溢出效应和波动溢出效应,结果如下:
(1)NCFI和EXP的波动持续性较强,两个市场都对自身前期波动的依赖性较高,波动集聚性明显。即市场每一时期所产生的变化不可能被立即“熨平”,或多或少会对自身以后的发展产生影响。国际航运市场和国际贸易市场的自我调节能力较弱,目前“高运价”和“高出口贸易需求”的状态仍将持续一段时期。建议时刻监测两个市场的运行动态,适时采取合理的风险防范措施:一是通过进一步完善对外开放体制机制,落实稳外贸政策,保障国际贸易市场的稳定;二是通过加大航运资源要素的配置能力和调控力度,保障国际航运市场的平稳运行。
(2)NCFI与EXP之间呈时变正相关关系,总体相关性不高,但后期有动态上升的趋势。国际贸易是国际航运的基础,国际航运是国际贸易的主要运输方式,两个市场同进退的关系增强。疫情影响下,国外供应链基本陷入停滞,中国作为全球制造业中心的地位愈发显著。中国生产的生活用品、防疫物资、工业品等通过海运大量向海外出口,国际航运与国际贸易的关系日益紧密。
(3)NCFI对EXP存在显著的单向格兰杰因果关系和单向波动溢出效应,NCFI是波动溢出的源头,也是风险溢出的源头。国际航运市场的平稳有序波动能显著促进国际贸易市场高质量发展。从目前市场表现看,国际航运市场的波动已经对国际贸易市场产生了一定制约,国际集装箱航运市场出现了一箱难求、一舱难求的现象,运费暴涨,导致大量订单被取消或延迟。2021年8月,中国制造业采购经理人指数之新出口订单指数已经连续4个月处于荣枯线以下。换言之,国际集装箱航运市场的缺舱、缺箱现象已经减缓了出口贸易的增长。2021年1月,宁波市政府针对国际航运市场的缺舱、缺箱和运价上涨过快现象,出台了10条应对举措,其中包括安排4 000万元专项资金用于第1季度的调运力、增空箱工作。该政策取得了明显的成效:宁波地区2021年1月空箱紧缺状态明显好转,2月和3月空箱需求得到满足;宁波口岸2021年1月和2月出口额同比增长42.7%,3月同比增长17.6%,4月借助政策余温同比增长32.6%。随着政策效应的消失,宁波地区2021年5月重回空箱紧缺状态,出口额同比增速开始逐月下降。因此,作为应对举措,国家有关部门和物流链相关方应先侧重于稳航运,帮助当前国际集装箱航运市场走出缺舱、缺箱和运价持续上涨的困境,维护国际供应链的稳定,促进贸易畅通。
