需求波动下多目标多周期内陆港动态布局优化
2023-01-03赵旭黄静韵张瑶
赵旭, 黄静韵, 张瑶
(大连海事大学交通运输工程学院, 辽宁 大连 116026)
0 引 言
内陆港作为连接内陆腹地与海港的重要纽带,为货主提供订舱、报关、报检等一站式服务。内陆港将腹地货物通过铁路运输集中运至海港,从而实现规模效益[1]。优化内陆港布局,有利于缓解海港吞吐压力,降低系统总成本,减少碳排放量,增强对货主的吸引力,提高内陆运输网络的效率。
内陆港布局优化研究中,大多是关于内陆港的静态选址研究:张兆民[2]采用模糊C均值聚类算法研究内陆港选址。梁承姬等[3]分析了地理位置因素和经济因素,构建集合覆盖模型和模糊聚类模型来确定最优内陆港选址。裴健[4]研究海上丝绸之路背景下的双层内陆港布局优化,并以华东地区为例进行分析。梁承姬等[5]考虑内陆港的规模经济效应,构建了带有成本折扣系数的选址模型,并采用混合遗传算法求解宁波港的内陆港选址。汪传旭等[6]以海港收益最大为目标,考虑内陆港中转比例和服务时间约束,决策多周期内陆港选址,但未考虑内陆港的容量限制。然而,内陆港的容量将直接影响其布局规划和需求点的路径分配。常征等[7]考虑内陆港的通过能力限制,以总成本最低为目标,构建两阶段选址模型。WANG等[8]在考虑内陆港的最大容量限制的基础上,加入最小容量限制以保证基本的吞吐量,建立了以系统总成本最低为目标的选址模型。随着绿色运输理念的兴起,ROSO[9]对比了有内陆港与没有内陆港的内陆运输系统模型,研究表明开放内陆港可以减少碳排放量,缓解码头拥堵。常征等[10]建立了考虑环境约束的双目标内陆港选址模型,结果表明系统总成本和内陆港数量越小,碳排放量越大。魏海蕊等[11]考虑海港与内陆港的合作关系以及拥堵与碳排放等环境因素,构建合作成本折扣评价模型,从整体视角对内陆港进行系统规划。考虑到需求的波动,范厚明等[12]以需求情景来描述需求的不确定性,以路径失灵概率描述可靠性,建立鲁棒选址模型对内陆港进行一次性选址以降低投资风险。TSAO等[13]采用模糊多目标规划方法进行不确定环境下的内陆港布局优化,该方法降低了1.14%的系统总成本,提高了计算效率。
现有研究为内陆港的布局优化提供了较好的基础,但大多关注的是固定容量的、单周期的一次性内陆港选址布局。考虑到内陆港布局是长期的战略决策,其间需求会因经济与政策的影响而波动,本文进行需求波动下多目标多周期内陆港动态布局优化研究。
1 问题描述
内陆货运需求是动态变化的,仅考虑单周期的一次性内陆港选址布局无法兼顾较长规划期内需求的波动。当需求增长时,部分货物无法通过内陆港进行转运,需要采用公路运输的方式直达海港,这将产生较高的运输成本和碳排放量,不利于内陆运输网络的绿色可持续发展;反之,当需求减少时,部分内陆港由于竞争力不足,利用率低下,造成资源浪费,产生额外运营成本的支出。
本文研究的多周期内陆运输网络示意图见图1。从内陆需求点中筛选出内陆港备选点,设置符合备选点辐射范围、经济发展水平以及人力物力资源情况的不同备选容量,并根据内陆港容量大小和所处城市设定新建成本、关闭成本、再建成本、容量调整成本和运营成本。以包括上述成本和运输成本的系统总成本、碳排放量和客户满意度最优为目标,根据需求波动进行内陆港动态布局优化,加入容量等级选择决策,确定内陆港在不同周期的新建、关闭、再建以及容量调整方案,并对需求点进行路径分配。

2 模型构建
2.1 模型假设
内陆需求点和内陆港备选点已知;内陆需求点的货物均采用集装箱运输;需求点在不同周期内的需求量不同;内陆港的新建、关闭、再建、容量调整成本以及运营成本与其容量大小及所处城市相关;每个需求点必须从内陆港中转运输和直达海港运输中选择一种运输模式;需求点至内陆港或直达海港采用公路运输方式,内陆港至海港采用铁路运输方式;不考虑运输通道能力限制。
2.2 符号说明
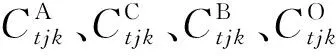
决策变量:Xtjk,若第t周期开放容量等级为k的内陆港j,则Xtjk=1,否则Xtjk=0;Ytij,若第t周期需求点i选择内陆港j中转,则Ytij=1,否则Ytij=0;Ytio,若第t周期需求点i选择直达海港o, 则Ytio=1,否则Ytio=0;Ztj,若第t周期内陆港j调整容量,则Ztj=1,否则Ztj=0。
2.3 模型建立
模型目标函数见式(1)~(3)。式(1)表示系统总成本(包括新建成本CA、关闭成本CC、再建成本CB、容量调整成本CE、运营成本CO和运输成本CT)最低;式(2)表示运输及内陆港中转过程中产生的碳排放量最小;式(3)表示客户满意度最大。
minC|C=CA+CC+CB+CE+CO+CT
(1)
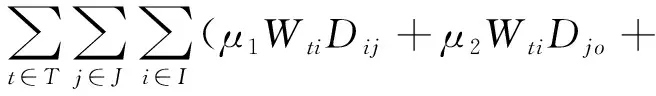
(2)
(3)
其中,

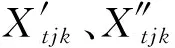
客户满意度与服务时间的关系为
模型约束条件如下:
式(4)表示只有内陆港开放时,货物才能通过该内陆港进行中转;式(5)表示每个需求点只能选择内陆港中转或直达海港中的一种运输模式;式(6)表示每个备选内陆港只能选择一种容量等级;式(7)表示内陆港的容量约束;式(8)表示海港的吞吐量约束;式(9)为0-1变量约束;式(10)为变量下标约束。
3 求解算法
带精英策略的非支配排序遗传算法(elitist non-dominated sorting genetic algorithm,NSGA Ⅱ)是基于Pareto的多目标进化算法,主要通过引入快速非支配排序方法、拥挤度计算和精英保留策略,达到降低计算复杂度、保证种群多样性和提高计算效率的目的[14]。针对模型特点,对NSGA Ⅱ进行改进:首先,染色体采用双层编码方式进行内陆港布局和路径选择决策;其次,为简化非法基因的修改操作,提升算法的求解效率,在开放的内陆港容量至少满足其所在城市的需求量的基础上,提出基于最近邻思想的交叉算子和变异算子;最后,在Pareto最优解集中,采用模糊决策选出最优解。
3.1 编码方式
染色体的双层编码方式见图2。第一层编码长度为备选内陆港数|J|与周期数|T|的乘积,可以一体化决策各周期备选内陆港的开关和容量等级。ktj=0代表第t周期内陆港j不开放;ktj=1,2,…,|K|代表第t周期内陆港j开放且其容量等级取值范围为{1,2,…,|K|}。第二层编码长度为内陆需求点数|I|与周期数|T|的乘积,Lti代表需求点选择中转的内陆港编号。

图2 染色体的双层编码方式
3.2 基于最近邻思想的改进
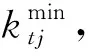
3.3 选择、交叉和变异操作
采用二元锦标赛选择法,每次从种群中选取2个个体,其中适应度更好的个体将进入子代种群。重复该操作,直到子代种群达到原种群规模。此方法有利于并行化处理,避免陷入局部最优解,且无须进行全部适应度值的排序步骤,具有更低的算法复杂度。
采用两点交叉法。在两个编码串中随机设置两个交叉点,交换两点间的部分基因。交叉后出现无法满足其所在城市需求的容量等级基因时,从“近邻城市组”中随机选取满足条件的基因进行替代。
采用基本位变异,在个体编码串中随机指定基因进行变异运算。变异后出现非法基因时,从“近邻城市组”基因中,选取出现次数较少且满足自身所在城市需求量的容量等级,增大其成为变异基因的概率。
3.4 模糊决策
采用改进的NSGA Ⅱ求得Pareto 最优解集后,决策者可以根据3个目标的重视程度来选取最优布局方案。为便于对比单周期布局与多周期动态布局对3个目标的优化程度,本文应用模糊理论的思想,选取隶属函数值Ax最大的解作为最优解,即

3.5 算法步骤
步骤1参数初始化。随机生成种群规模为m的初始种群P0,作为父代种群。
步骤2对种群P0进行快速非支配排序分层,计算每个个体的拥挤距离。
步骤3基于个体的非支配排序等级和拥挤距离,采用二元锦标赛方式从种群P0中选取个体,进行两点交叉和随机变异操作,得到种群规模为m的子代种群P1。
步骤4将父代种群P0与子代种群P1合并,生成规模为2m的新种群P2。
步骤5对种群P2进行自然选择,以η的概率淘汰劣解,生成与父代种群规模一致的新种群P3,再次返回步骤2。直到满足最大迭代次数,得到Pareto非劣解集合。
步骤6对第一非支配层进行模糊决策,得出最优解。
4 算例求解与分析
4.1 数据收集
本算例对东北地区内陆港进行多目标多周期动态布局优化。内陆港运营以5年为一个周期,周期数k=3。从28个需求点筛选出16个内陆港备选点,根据各备选点的辐射范围、经济发展水平以及人力物力资源情况,设定适合其实际情况的多个容量等级[15]。参照已建设完成的内陆港相关成本[16],估算出各备选内陆港对应不同容量等级的新建成本、关闭成本、再建成本和运营成本,见附表1。由于东北地区98.5%以上的外贸集装箱货物经由大连港出口,因此海港选为大连港。
根据式(11)将2006—2020年内28个内陆城市的出口额数据转换为运输需求量,对需求量的分布函数进行拟合,估算出2021—2035年内3个周期的运输需求量。
W=VA1A2
(11)
式中:W为出口集装箱需求量,TEU;V为出口额,万美元;A1为出口适箱货金额比重,取值为80%;A2为出口适箱货生成系数,取值为0.35 TEU/万美元。
根据原铁道部对运价的规定及《国际集装箱汽车运输费收规则》,铁路和公路运价分别为3.185元/(TEU·km)和8元/(TEU·km)。内陆港的中转费用为120元/TEU。公路运输碳排放因子μ1取3.704 kg/(TEU·km),铁路运输碳排放因子μ2取 0.158 kg/(TEU·km)[17],在内陆港中转的碳排放因子μ3取5.8 kg/TEU[18]。算法的种群规模取100,最大迭代次数取1 000,交叉概率取0.8,变异概率取0.1,接受劣解的概率取0.1。
4.2 模型求解及分析
通过MATLAB 2020a利用改进NSGA Ⅱ求解模型,得出东北地区内陆港的多周期动态布局和单周期布局及服务城市,分别见表1和2。单周期布局是根据第一周期的需求进行决策得到的,后期不再进行动态调整。在单周期布局下,若内陆港无法满足增长的需求,则部分货物只能选择公路运输直达海港;若内陆港后期货量短缺或竞争力不足,但仍继续维持原有容量规模开放,则会造成资源浪费。内陆港利用率为通过的货量总和占内陆港容量的比值,对比可以看出,多周期动态布局下的内陆港具有较高的利用率,可以有效减少资源浪费。

表1 东北地区内陆港多周期动态布局及服务城市

表2 东北地区内陆港单周期布局及服务城市
内陆港多周期动态布局优化以5年为一个周期,因此内陆港的周期容量为年容量的5倍。第一周期,在原容量分别为125万TEU、50万TEU的沈阳、哈尔滨内陆港基础上,新建鞍山、佳木斯内陆港,容量分别为50万TEU和25万TEU,原长春和牡丹江内陆港的容量由75万TEU分别缩小至50万TEU和25万TEU,关闭货源不足的吉林内陆港;第二周期,沈阳、哈尔滨内陆港容量不变,新建容量为15万TEU的朝阳内陆港,鞍山、长春内陆港的容量由50万TEU分别增大至75万TEU和100万TEU,佳木斯内陆港的容量由25万TEU增大至50万TEU,关闭牡丹江内陆港;第三周期,沈阳、朝阳、佳木斯内陆港容量不变,新建容量为50万TEU的本溪内陆港,对第一周期关闭的吉林内陆港进行再建,容量为40万TEU,哈尔滨内陆港的容量由50万TEU增大至60万TEU,鞍山、长春内陆港的容量分别由75万TEU、100万TEU缩小至50万TEU、75万TEU。
需求量随着经济发展状况和政策的变化而波动,从而对内陆港布局产生影响。首先,当沈阳、鞍山、本溪、朝阳、长春、哈尔滨、佳木斯等内陆城市需求量明显增大,而相应内陆港容量不足时,货物通过公路直达运输至海港将产生较高的碳排放量和运输成本,因此及时新建内陆港,或者扩大原有内陆港的容量,可以更好地满足增长的运输需求。其次,在需求减少时,采用关闭相应内陆港、缩小容量或更换更具有竞争力的内陆港等措施,可以保证现存内陆港的较高利用率,减少资源浪费和运营成本的支出。最后,布局调整中还存在关闭后再建的内陆港,如吉林内陆港:在第一周期,吉林内陆港附近竞争力更强、辐射范围更广的长春内陆港将容量降至最小等级后,仍足以服务吉林市的所有需求,因此关闭吉林内陆港以节省运营成本;在第二、第三周期,随着长春及其服务城市的需求逐步增大,再建吉林内陆港可以有效分担长春内陆港的货量。
与单周期布局相比,多周期动态布局根据需求波动做出动态调整,需要花费更多的新建成本、关闭成本、再建成本以及容量调整成本,但逐步优化后的内陆港布局更符合不断变动的实际需求分布,从而优化了系统总成本,具体表现为:需求增加时,货物经新建或增大容量的内陆港中转后通过铁路运输集中转运至海港,相比公路直达运输能节省更多的运输成本;需求不足时,关闭内陆港或缩小内陆港容量可以减少不必要的运营成本支出。相比全程公路运输,经内陆港中转后采用铁路运输更有利于碳排放量的优化,缓解海港拥堵情况,从而使货物在期望服务时间内送达,提升客户满意度。从表3的运行结果可以看出,在长达15年的3个周期内,东北地区内陆港的多周期动态布局比单周期布局节省了67.62亿元的系统总成本,减少了64.49亿kg的碳排放量,客户满意度提升了18.55%。

表3 东北地区内陆港多周期动态布局与单周期布局优化模型的运行结果对比
5 结 论
本文研究了需求波动下的多目标多周期内陆港动态布局优化,以系统总成本、碳排放量和客户满意度最优为目标,建立内陆港多目标多周期动态布局优化模型,确定不同周期内陆港的新建、关闭、再建以及容量调整方案,并对需求点进行路径分配。设计带有双层编码方案和由最近邻思想改进的NSGA Ⅱ求解模型。东北地区内陆港布局优化结果表明:与单周期布局相比,多周期动态布局能根据需求波动做出动态调整,通过节省运输成本与运营成本从而降低系统总成本,有效减少碳排放量,提高客户满意度和内陆港利用率,有利于内陆运输系统的绿色、高效、可持续发展,可为需求波动下的多目标多周期内陆港动态布局优化提供参考。
在内陆港布局优化问题上,与以往将内陆港最大容量设为定值不同,本文加入容量等级决策,并根据容量大小设定内陆港的新建、关闭、再建、容量调整和运营成本,使求解结果更能反映实际情况;在动态布局优化调整中,不仅考虑了新建内陆港的情况,还对原有内陆港进行关闭、再建以及容量调整决策,使逐步优化后的内陆港布局更符合不断变动的实际需求分布。下一步的研究方向是考虑多港口竞合下的内陆港多周期动态布局。
