考虑多维特征的船舶轨迹分层聚类算法
2023-01-03苏俊杰兰培真
苏俊杰, 兰培真
(1. 集美大学海上交通安全研究所, 福建 厦门 361021;2. 交通安全应急信息技术国家工程实验室, 福建 厦门 361021)
0 引 言
航运经济的发展促使船舶数量日益增加。船舶自动识别系统(automatic identification system,AIS)作为船与船、船与岸之间船舶相关信息的交换设备在船舶监管中广泛应用,产生了海量的船舶动静态信息数据,而提取特征相似的船舶运动轨迹簇是分析船舶交通规律和船舶行为模式的基础[1],因此,急需开展船舶轨迹的聚类研究。早期轨迹聚类研究[2-3]以轨迹点为样本,忽略了相邻轨迹点的时空关联,因此近期研究样本大多为由连续点构成的轨迹段。陈锦阳等[4]通过设定Hausdorff距离阈值划分轨迹类别,类似指标还有欧氏距离、最长公共子序列距离、动态时间规整(dynamic time warping,DTW)距离等,然而这些指标只考虑船位偏差,描述船舶相似运动的能力有限。刘磊等[5]考虑船位、航速和航向定义综合距离,并以K最邻近分类器划分轨迹;王维刚等[6]以8个轨迹特征度量轨迹相似性,设计了加权朴素贝叶斯分类器,证明了考虑多维特征度量相似性能更好地捕捉不同轨迹的差异[7]:这些监督分类方法在航路固定时表现较好,但要求提供准确的先验知识且难以发现隐蔽轨迹簇,无法满足多数聚类情况的需要。因此,以具有噪声的基于密度的空间聚类(density-based spatial clustering of applications with noise, DBSCAN)算法[8-11]为典型的无监督聚类方法的应用较多。然而,全局性的经验参数难以在密度不均的船舶交通环境下对各局部进行合理的聚类,为此,赵梁滨等[12]通过层次聚类获取局部密度环境的适应参数。此外,LI等[13]在K均值聚类算法的基础上提出自适应K值的多步轨迹聚类算法,但该算法直接处理整条轨迹,时空复杂度较高且丢失了轨迹的局部相似性;马文耀等[14]采用谱聚类(spectral clustering,SC)算法区分船舶在不同行为模式下的轨迹;牟军敏等[15]提出船舶轨迹的自适应SC算法,但船位偏差仍是相似性度量的唯一依据;冷泳林等[16]以线型特点衡量轨迹的相似性,并以仿射传播(affinity propagation,AP)算法进行聚类,但聚类后的船舶运动轨迹相似性较低。针对上述船舶轨迹聚类方法存在的不足,本文提出一种考虑多维特征的船舶轨迹分层聚类(multi-features hierarchical clustering, MHC)算法,主要由分层轨迹相似性度量和CFA-DBSCAN算法2部分构成,这里CFA(core firefly algorithm)指核心萤火虫算法。
1 轨迹相似性度量
船舶运动惯性大,船舶行为模式具有区域性[10],相似轨迹应为相似水域内轨迹线型特点相似且具有相似航行动态的轨迹,因此以地理网格和时段作为轨迹段的划分依据。任意轨迹可表示为T=(p1,p2,…,pN),其中:N为轨迹点数;pi为i时刻的船舶运动状态,是由经度λi、纬度φi、航速vi、航向αi和时隙Δti构成的5维特征向量,即pi=(λi,φi,vi,αi,Δti)。轨迹T的线型特点及轨迹所处水域环境可由轨迹线型图F1和水域信息图F2描述,其中:F1为各轨迹点按顺序连接而成的曲线图;F2为轨迹所处地理网格范围内的地图图像。以图1为例说明水域信息图的构建过程。为保证聚类结果的合理性,应尽量选择噪声点少的,即同类地理环境区分度低、异类地理环境区分度高的地图图像数据。因为遥感影像包含的噪声点较多,容易降低不同水域环境的辨识敏感度,所以本文研究区域的水域信息图采用如图1a所示的公开地图图像数据。地理网格的设置应使得轨迹段的点数和水域信息图采样范围合理,采用图1b所示5×5地理网格将原始轨迹划分到18个水域,即首先使由地理网格划分的各轨迹段包含轨迹点数在[500,1 000]内,其次使地理网格内的地图图像能达到粗略区分港口、沿岸和开阔水域的目的,则轨迹所处水域信息可用该水域范围内的地图图像表示。
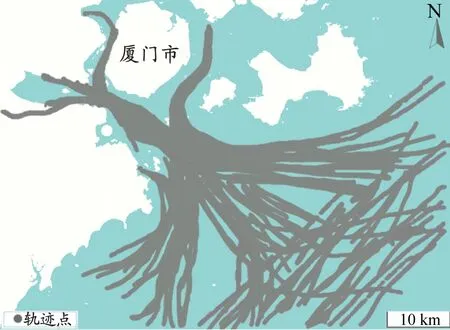
a)研究区域的船舶轨迹
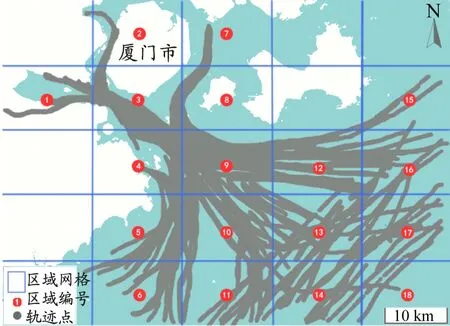
b)地理网格划分的水域
将船舶的多维特征划分为静态图像上层和动态数值下层,对不同层分别建立不同的轨迹相似性度量指标,经两次递进聚类逐步放大轨迹簇间的差异,最终实现隐蔽轨迹簇的辨识。MHC基本框架见图2,其中,SIFT(scale-invariant feature transform)指尺度不变特征变换算法。
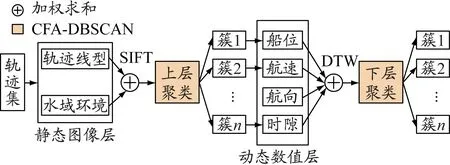
图2 MHC基本框架
1.1 静态图像上层
上层聚类特征为轨迹线型图和水域信息图,轨迹线型图和水域信息图均为64×64的灰度图像,各像素点取值区间为[0,255]。SIFT算法[17]鲁棒性强,在光照、旋转、视点和仿射变换条件下均能保持优良的稳定性,故采用SIFT算法建立上层相似性的度量指标。如图3所示,SIFT算法本质上是将图像相似性转换为2张图像所有匹配特征点的相似性,因此,需要检测图像包含的所有特征点,并为每个特征点生成描述符。
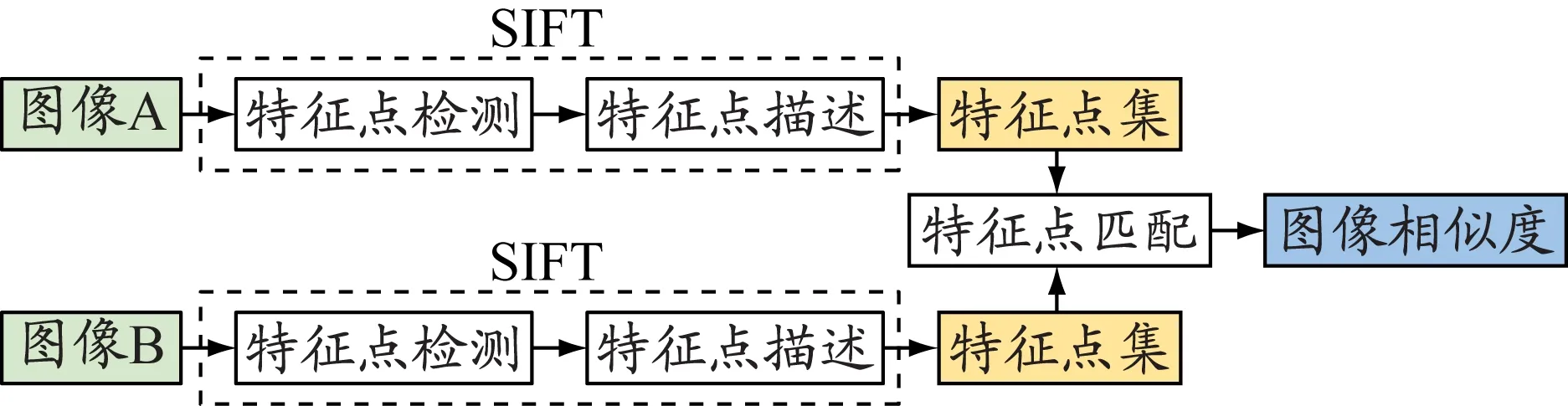
图3 SIFT算法基本框架
特征点检测阶段需要确定特征点所在的尺度和位置。以图4为例说明图像特征点的检测过程。给定图像I(x,y)和尺度高斯变换函数G(x,y,σ)(σ为采样尺度),可构建图像的尺度空间L(x,y,σ)。尺度空间是由不同分辨率图像构成的高斯金字塔,用于描述图像的尺度不变性。
(1)
L(x,y,σ)=G(x,y,σ)*I(x,y)
(2)
式中:σ取1.6;*为卷积运算。
高斯差分尺度空间D(x,y,σ)为相邻尺度的高斯差分与原图像的卷积,特征点由高斯差分尺度空间的局部极值点构成。为寻找局部极值点,一个像素点要与其所有的相邻点比较,看该像素点是否比其图像域和尺度域的相邻点大或者小。如图4c所示,检测点需要与26个点(与检测点同尺度图像域的8个相邻点+与检测点上下相邻尺度图像域的9×2个点)进行比较,以确保在尺度空间和图像空间都检测到极值点。
D(x,y,σ)=
(G(x,y,kσ)-G(x,y,σ))*I(x,y)
(3)
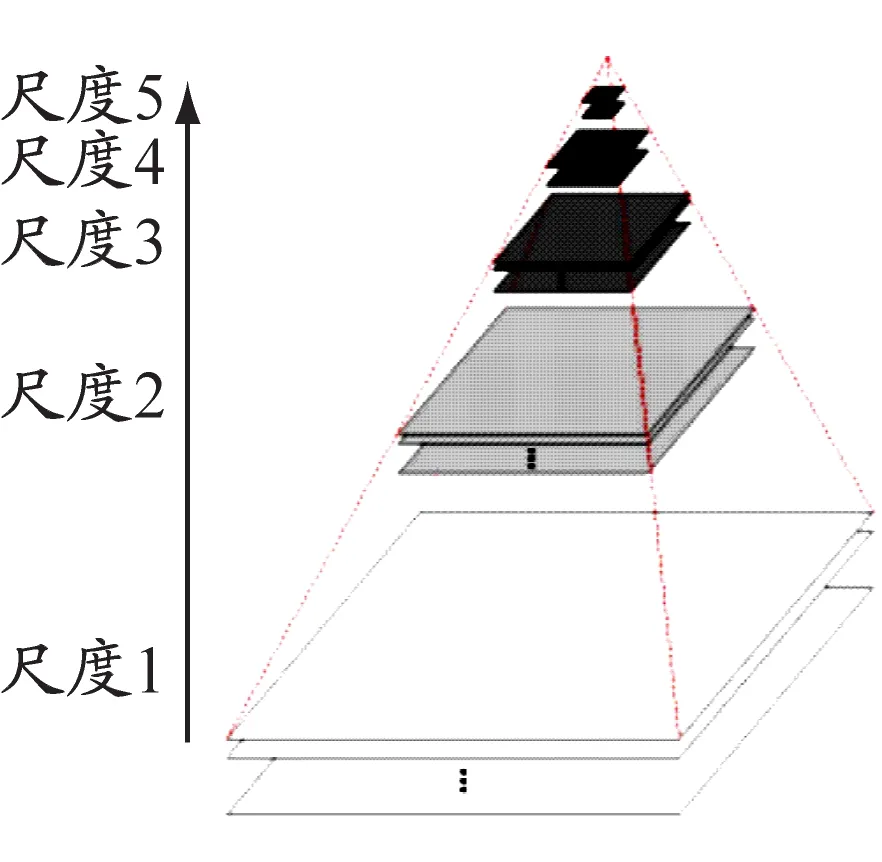
a)高斯金字塔
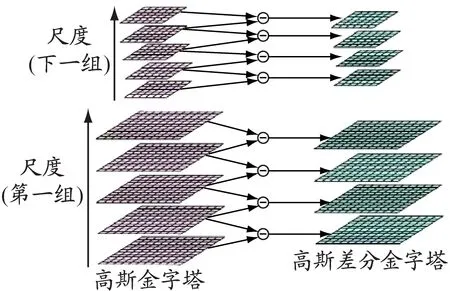
b)高斯差分金字塔
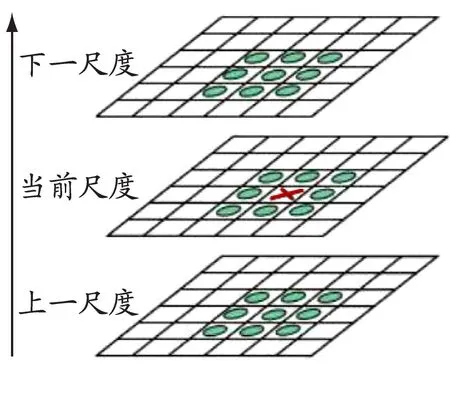
c)特征点
特征点描述阶段需要为每个特征点生成对应的特征描述符,即以特征点邻域像素的梯度方向分布赋予特征点方向信息,L尺度下(x,y)处的梯度值m(x,y)和方向θ(x,y)分别为
m(x,y)=((L(x+1,y)-L(x-1,y))2+
(L(x,y+1)-L(x,y-1))2)1/2
(4)
(5)
以图5为例说明特征描述符在实际应用中的构建。首先将特征点的邻域像素划分为2×2的区块,每个区块由4×4子域构成,计算每个子域的梯度并统计各区块内8个方向(每个方向的范围为0~45°)的梯度方向直方图,其中,纵轴为每个梯度方向的梯度累计值,则每个区块可描述为一个8维的向量,该特征点的特征描述符为一个2×2×8维的向量。
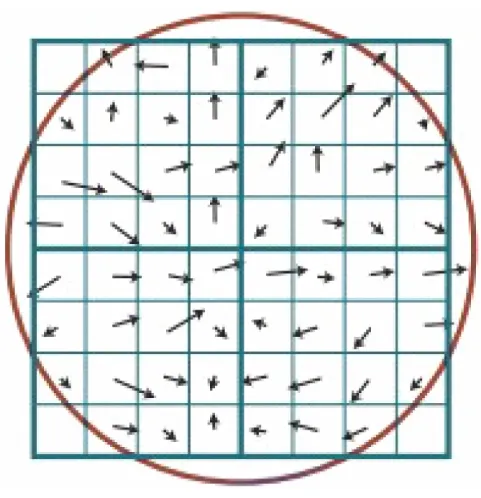
a)图像梯度
b)统计直方图
c)关键点描述
特征点匹配旨在寻找两张图像匹配的特征点对,匹配度量为特征描述符的余弦距离。匹配特征点对的查找方法:检索某图像特征点在另一图像中的最邻近和次邻近特征点,若最近距离与次近距离的比值小于给定阈值(通常取0.6~0.8[18]),则该特征点与最邻近特征点匹配。图像距离为所有匹配特征点对余弦距离的平均值。上层船舶轨迹相似性可用轨迹线型图和水域信息图图像距离的均值Dimg度量。
(6)
式中:d1为轨迹线型图的图像距离;d2为水域信息图的图像距离。
1.2 动态数值下层
下层聚类特征为船位、航速、航向和时隙,轨迹相似性即轨迹运动特征的相似性。船舶轨迹是不等长的时序数据,因此,采用DTW[10]算法建立下层轨迹相似性的度量指标。以图6为例说明下层轨迹相似性的计算过程:给定任意两条船舶轨迹TA和TB,构建初始距离矩阵,该矩阵的元素d(i,j)为对应两轨迹点特征向量的余弦距离。余弦距离按式(7)计算,计算前需将各特征分量进行归一化以消除不同量纲的影响。按式(8)计算初始距离矩阵的累积距离矩阵,即累积距离矩阵中Mc(i,j)的值等于其左、上和左上位置数值中的最小值与初始距离矩阵对应位置之和。下层轨迹的相似性可由遍历轨迹TA和TB所有轨迹点的最小累积距离Mc衡量。
(7)
Mc(i,j)=d(i,j)+min(Mc(i-1,j-1),
Mc(i,j-1),Mc(i-1,j))
(8)
式中:xik和xjk分别为点pi和pj的第k个特征分量。通常d(i,j)越小,pi与pj越相似。假设pi=(1,1,0,0,1),pj=(1,1,1,0,1),则根据式(7)有
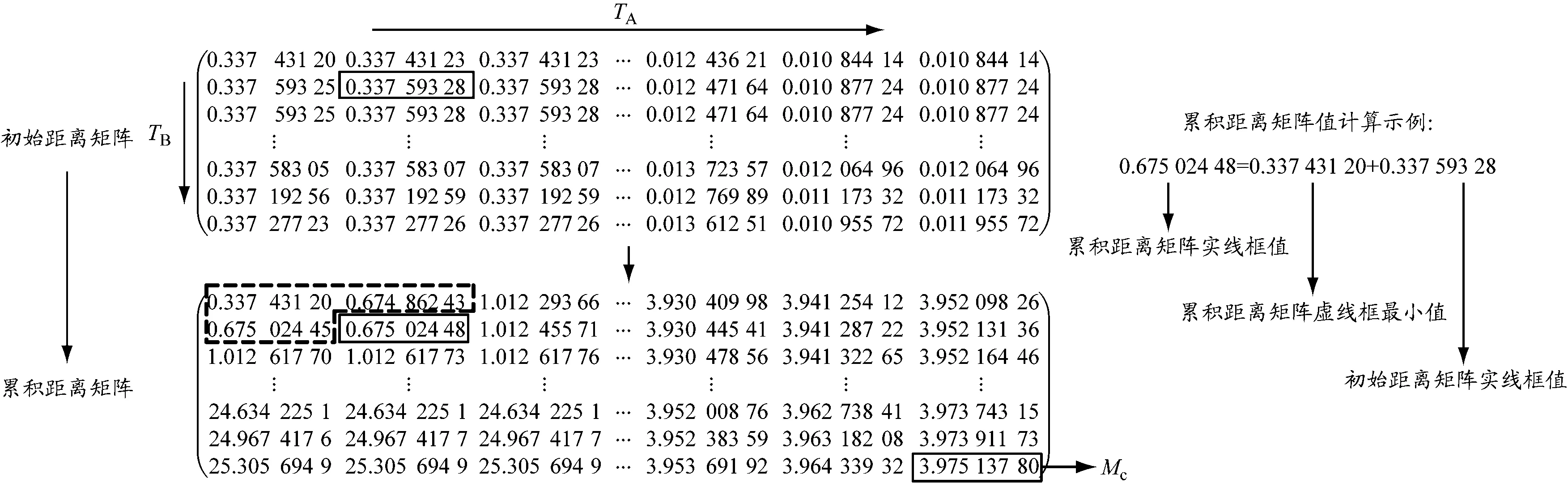
图6 累积距离矩阵计算
2 CFA-DBSCAN算法
2.1 改进DBSCAN算法
DBSCAN算法是基于密度的无监督聚类算法[19],辨识隐蔽簇的能力强且无须设定簇的数量,适用于船舶轨迹数据噪声点多、船舶行为模式不确定性高的情况,相关定义如下:
定义1核心样本:对某样本li,若在给定距离半径r的邻域ε(li)中样本的数量不低于给定阈值δ,则该样本为核心样本。
定义2密度直达:某核心样本可密度直达其邻域包含的所有样本。
定义3密度可达:若li密度直达lk,lk密度直达lj,则li密度可达lj,即若某核心样本li密度直达的样本lk为核心样本,则样本li密度可达lk邻域的所有样本,密度可达具有传递性。
定义4密度相连:若核心样本lk密度可达li和lj,则li与lj密度相连,即由密度可达的所有核心样本的邻域构成的区域内的样本都密度相连。
DBSCAN算法旨在将密度相连的样本聚成同簇,而在实际聚类过程中,样本邻域通常存在交集。为避免DBSCAN的重复查询,仅聚类核心样本,对同簇的核心样本集对应的邻域样本集取并集来进行簇的扩充。
2.2 CFA
改进的DBSCAN算法同样对参数的设置比较敏感,因此,基于萤火虫算法(firefly algorithm,FA)[20]来优化参数。FA是新兴的群智能优化算法,概念简单、优化性能好,在参数调优问题上应用广泛。FA基本步骤[21]如下:
步骤1初始化萤火虫数量N,最大吸引度β0,光吸收系数γ,步长因子ρ,ρ∈[0,1],最大迭代次数tmax和搜索精度ξ。
步骤2随机初始化萤火虫位置,计算目标函数值S作为萤火虫各自的最大荧光亮度I0。
步骤3计算群体中萤火虫的相对亮度I和吸引度β,相对亮度决定萤火虫的移动方向。
(9)
式中:rij表示萤火虫i与j的距离;β0为最大吸引度,即rij=0时的吸引度。
步骤4更新萤火虫被吸引后的位置。
xi(t+1)=xi(t)+β(xj-xi)+ρ(μ-0.5)
(10)
式中:t为迭代次数;μ为[0,1]内均匀分布的随机因子。
步骤5更新萤火虫的亮度。
步骤6若达到最大迭代次数或满足搜索精度,则转下一步;否则重复步骤3~6。
步骤7输出全局极值点和个体最优亮度值。
FA缺乏全局随机性,易陷入局部最优[20]且萤火虫群位置的频繁更新使得算法时空复杂度较高,因此,提出CFA。区别于FA,CFA只选取亮度排在前20%的萤火虫作为核心萤火虫进行位置更新,并随机分配其余萤火虫的位置来确保全局随机性;在没有局部更亮的个体时,核心萤火虫会向种群的全局最优点移动,最优位置即核心萤火虫的收敛位置。为避免随着迭代次数增加,核心萤火虫围绕最优位置振荡,按式(11)分段设置步长因子。
(11)
式中:ρ0为初始步长因子,ρ0∈[0,1];lij为萤火虫i与j在不同维度上的距离。
2.3 CFA-DBSCAN算法
CFA-DBSCAN算法为改进DBSCAN算法与CFA参数寻优算法的结合,即采用CFA优化改进DBSCAN算法的参数r和δ以获取当前最优的轨迹聚类效果。为寻求参数r和δ的最优值,定义参数优化的目标函数为轨迹聚类的总轮廓系数S[22],即使得同簇内样本相似度最大,不同簇间的相似度最小[23]。其中,S取值越接近1说明算法聚类性能越好。
式中:s(i)为轨迹的轮廓系数;a(i)为样本i与同簇内其他样本的平均距离;b(i)为样本i与不同样本的平均距离;NS为样本总数。
3 检验分析
以厦门港及其附近水域的AIS数据来验证MHC算法的有效性。AIS数据集包含船舶轨迹2 364条。为确保检验分析结果的准确性,参考ZHAO等[24]提供的方法对采集的AIS轨迹数据进行预处理,先用地理网格划分船舶轨迹,再按小时时段划分船舶轨迹,得到有效轨迹段共5 006条。该轨迹数据集的时间跨度为20190815T114425—20190820T114425,地理跨度为东经117°54′37″~118°36′39″,北纬24°06′38″~24°31′37″,航速范围为0~14 kn,航向范围为0°~359.9°。
为检验MHC算法的性能,以异常轨迹数、簇数、簇内DTW距离均值、簇间DTW距离均值和准确率为评价指标,对比分析MHC算法与CFA-DBSCAN、DBSCAN[25]、AP[16]、SC[14]、K均值聚类[13]等5种其他常用船舶轨迹聚类算法的评价指标值,见表1。5种其他常用算法均以船舶轨迹的DTW距离作为算法的样本距离;CFA-DBSCAN算法的参数按萤火虫种群规模N=100,最大迭代次数tmax=200,初始步长因子ρ0=0.8,光吸收系数γ=1设置;设定SC和K均值聚类算法的聚类簇数与MHC算法的聚类簇数相同。由表1可见,在无须事先设定簇数的聚类算法(MHC、DBSCAN和CFA-DBSCAN)中,MHC算法将轨迹聚为9簇,而DBSCAN算法和CFA-DBSCAN算法均只将轨迹聚为3簇,表明MHC算法能更好地辨识隐蔽轨迹簇。在将轨迹聚为3簇的算法中,CFA-DBSCAN算法的各指标均优于AP算法和DBSCAN算法,这表明根据经验设置的DBSCAN算法参数不足以区分复杂的船舶轨迹,而通过CFA确定的最优参数能在一定程度上提高DBSCAN算法的性能。在将轨迹聚为9簇的算法中,MHC算法在各评价指标上都优于SC算法和K均值聚类算法,簇内DTW距离均值为5.199,簇间DTW距离均值为18.032,准确率为91.50%,表明MHC算法能更好地辨识轨迹间的异同,从而实现船舶轨迹的准确聚类。
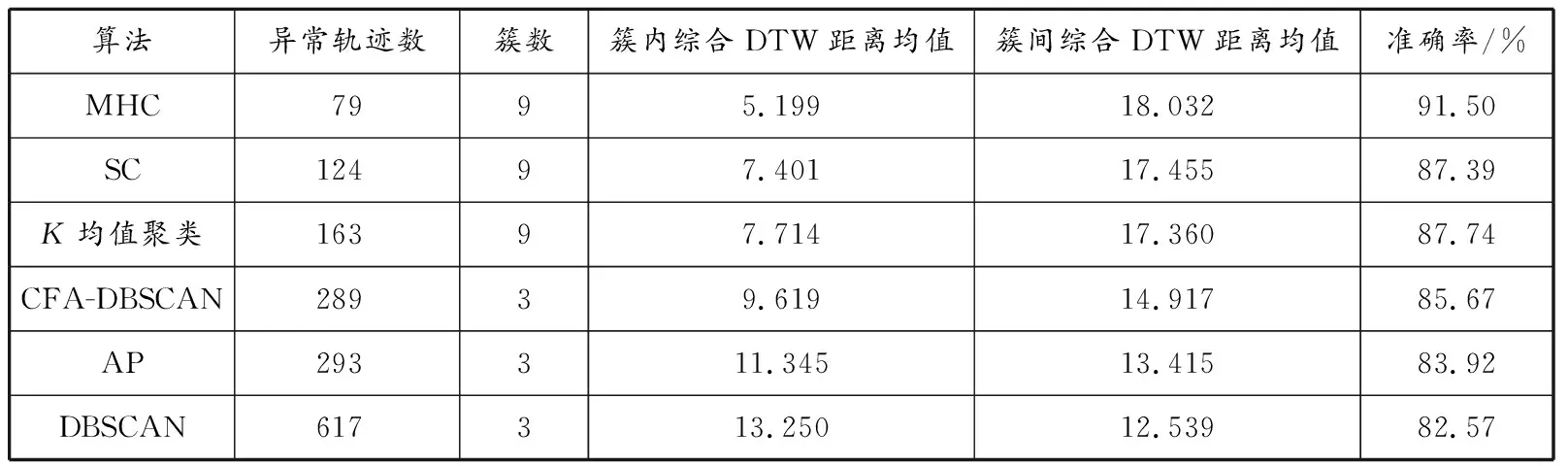
表1 各轨迹聚类算法的评价指标值
为分析MHC算法各模块在轨迹聚类过程中的影响,设置3组并行实验:第一组作为对照实验,仅考虑船位、航速和航向特征,并用DBSCAN算法对轨迹进行聚类;第二组实验将DBSCAN算法替换为CFA-DBSCAN算法;第三组实验在第二组实验的基础上引入水域环境、轨迹线型和时隙特征对船舶轨迹进行分层聚类。如图7所示:DBSCAN算法将船舶轨迹划分为3簇,基本对应着港区和外海的船舶,但局部轨迹分类明显不符合实际,如外海船舶被归到港区的船舶簇,且异常轨迹较多,聚类效果较差。这表明在较大水域环境范围内船舶轨迹通常密度不均,DBSCAN算法全局性经验参数的设置难以获取局部密度环境下的合理聚类,且在区分船舶行为多变的轨迹方面存在局限性。CFA-DBSCAN算法同样将船舶轨迹划分为3簇,但异常轨迹数明显减少,表明DBSCAN算法对参数的选取敏感,而通过CFA确定的参数能在一定程度上提高算法的质量。MHC算法通过上层聚类后得到3簇轨迹,基本对应着沿岸和外海曲度不同的船舶轨迹,异常轨迹相对较少,异常轨迹基本集中在水上交通环境复杂的港区;通过下层聚类后,船舶轨迹被划分为9簇,基本对应船舶进出港区的轨迹汇聚和轨迹分流,与目前厦门的船舶交通状况基本吻合,且异常轨迹明显减少。这表明MHC算法通过上层和下层递进聚类的方式能更好获取局部密度环境的适应参数。
表2为算法的运行指标。由表2可见:CFA-DBSCAN算法的邻域查询次数比DBSCAN的少,表明邻域查询部分的改进减少了聚类过程中的重复操作;CFA-DBSCAN算法聚类时间比DBSCAN算法的多,这是由于DBSCAN算法参数是事先设定的,不需要通过多次迭代更新,节省了聚类时间,而CFA-DBSCAN算法需要通过多次迭代使得轨迹聚类结果的轮廓系数收敛于全局最优;MHC算法需要的聚类时间比前两种算法的多,这主要是因为在传统船舶轨迹相似性考虑标准的基础上引入了水域环境、轨迹线型和时隙特征,增加了轨迹相似性度量复杂度,而图像相似度的计算和上下层递进聚类增加了轨迹相似性度量的时间和邻域查询次数,但也正是这些原因使得MHC算法更容易发现隐蔽轨迹簇,在聚类结果和准确度方面较优。
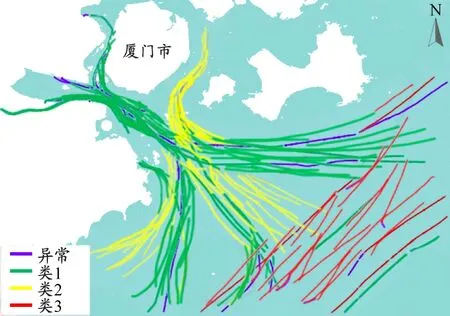
a)DBSCAN
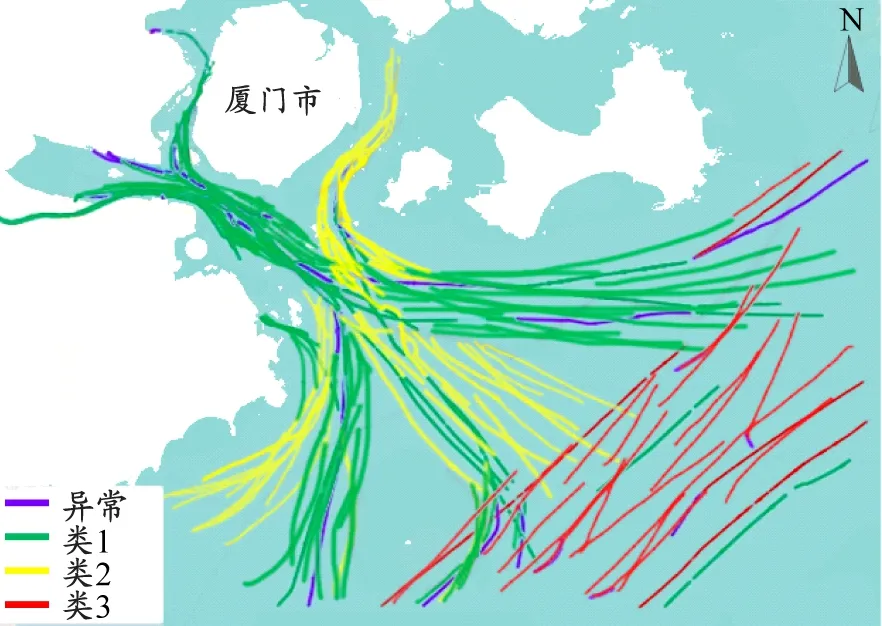
b)CFA-DBSCAN
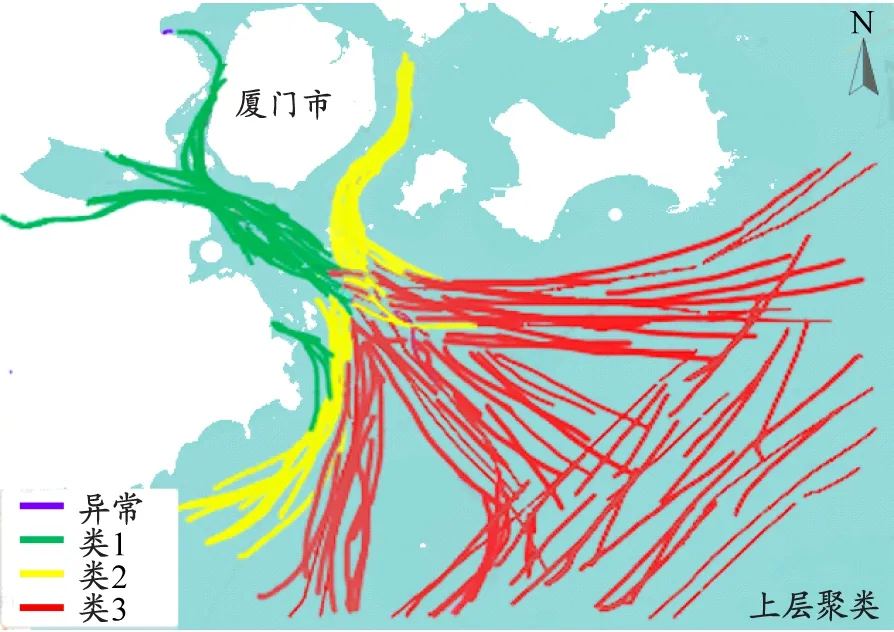
c)MHC上层聚类
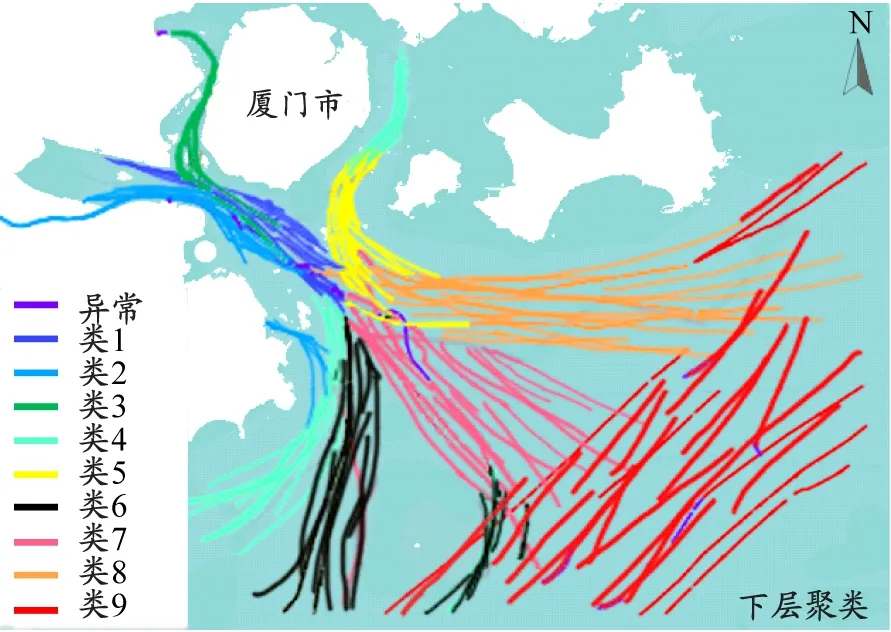
d)MHC下层聚类
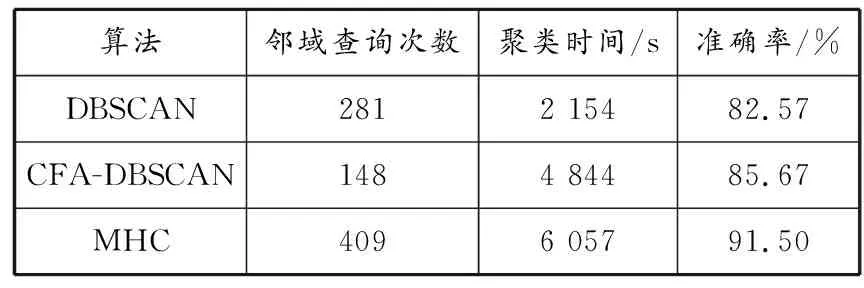
表2 轨迹聚类算法的运行指标
4 结 论
为准确聚类复杂的船舶轨迹和辨识隐蔽轨迹簇,本文提出考虑多维特征的船舶轨迹分层聚类(MHC)算法。在传统船舶轨迹聚类特征的基础上引入水域环境、轨迹线型和时隙特征分层建立轨迹相似性度量指标并以CFA-DBSCAN算法递进聚类各层轨迹,以厦门港及其附近水域AIS数据验证了MHC算法的有效性。检验结果表明,MHC算法相较于常用的聚类算法能更准确地区分船舶轨迹并发现隐蔽轨迹簇,聚类后同簇内轨迹的船舶运动特性更相似,而不同簇轨迹的船舶运动特性差异更明显。聚类结果可为船舶交通流特性分析和船舶行为模式识别提供精确的样本支持。MHC算法的聚类时间较长,因此,如何兼顾MHC算法聚类性能并优化聚类时间将是后续研究的重点。
