基于无序量测粒子滤波的无人船导航

古毅杰， 张闯， 康凯航

(大连海事大学航海学院， 辽宁 大连 116026)

0 引 言

无人船是能够在海洋、河流等环境中自主完成任务的平台，是自动驾驶技术在水面环境中应用的最主要体现[1]。全球导航卫星系统(global navigation satellite system，GNSS)作为现今船舶定位导航的关键手段之一，能够为无人船提供连续实时的导航解，但导航解的精度容易因卫星信号衰减等因素的影响而降低。船舶定位一般通过滤波技术递归计算后验概率密度，然后将其作为贝叶斯估计的近似值来解决。在实践中，经常会出现偏离真实状态的错误估计，如果无法恢复到正确的轨迹，则称这样的偏离为发散。众所周知，发散或者不可靠的估计是由建模误差引起的，包括非线性、偏差或者缺乏统计模型知识[2-4]。为解决非线性系统的估计问题，众多学者提出一些改进算法，如扩展卡尔曼滤波(extended Kalman filter，EKF)[5]、无迹卡尔曼滤波[6]和容积卡尔曼滤波[7]。这些方法提高了卡尔曼滤波算法求解非线性估计问题的能力，但都局限于高斯噪声的假设，因此对非高斯噪声的估计仍需进一步改进。粒子滤波(particle filter，PF)在非线性和非高斯滤波应用中被验证是有效的[8]，它是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法。它对过程噪声和量测噪声没有任何限制。PF的本质是用由有限个加权样本或粒子组成的离散随机样本近似表示概率分布。理论上，当样本量足够大时，PF可以逼近任何形式的状态变量的后验概率密度函数，因此，适用于任何可用状态空间模型表示的非线性非高斯随机系统。

常用的PF算法还存在一些严重的问题。当似然函数位于系统状态转移概率密度的尾部时，从重要性概率密度得到的样本与从真实后验概率密度得到的样本相差很大，从而导致粒子权重集中在少数粒子上，无法表示实际的后验概率分布。这称为PF的退化问题。解决此退化问题的主要方法是选取重要度较高的后验概率密度函数以及采用重采样方法。文献[9]利用无迹粒子滤波器(unscented particle filter，UPF)得到PF的重要性采样密度。常用的重采样技术包括多项式重采样、系统重采样和剩余重采样[10-11]。采用重采样方法虽然可以减少退化现象的发生，但会导致粒子多样性的损失。为保证粒子的多样性，学者们提出辅助变量PF[12]、重采样移动算法[13]、正则化PF[14]和基于智能优化的PF[15]。

PF也存在发散现象。作为发散监测的手段，Kullback-Liebler散度、非标准化权重和新息序列[16]被用来将观测结果与粒子云进行比较。如果检测到发散，通常利用最后一次可靠估计重新启动滤波器。特别是在含有坡度曲线标志变化拐点的非线性量测模型中，量测的模糊性被认为是导致滤波器退化和发散的重要原因，而且模糊量测更新会导致后验密度的发散。文献[17]研究了基于有序滤波框架的H∞滤波实现无序量测的更新，能够解决单步延迟的无序量测问题，但是无法解决非线性条件下的无序量测问题。文献[18]提出一种基于无序量测更新估计的信息滤波算法，通过对选择阈值与固定阈值的比较，丢弃无用的无序量测，从而在不影响滤波精度的条件下减少计算量。文献[19]针对非线性条件下的无序量测问题，讨论了快速边缘PF算法，采用无序处理思想分别估计线性和非线性目标运动状态矢量。PF中的多重模态分布使用混合粒子滤波(mixture particle filter，MPF)处理全局定位问题[20]，并且在初始位置不确定性较大时采用MPF。本文主要解决模糊量测更新的问题，模糊量测更新定义为导致粒子协方差增加的量测更新，进而模糊量测更新会导致粒子分散并提供不可靠的估计解。

本文主要研究取决于粒子先验分布量测模糊度的量测量。为获得精确的位置估计值，提出一种基于无序量测的PF(out-of-sequence measurement based PF, OOSMPF)算法，当量测量模糊或不足时跳过该时间步长的量测更新，而后用无序量测解弥补跳过的量测更新。最终，将本文提出的算法在无人船航行条件下与EKF、PF、MPF等方法进行比较，通过均方根误差估计证明本文提出的方法具有更优越的性能。

1 PF及模糊量测更新

1.1 PF

非线性随机系统可以用离散过程模型和量测模型[18-19]表示：

(1)

式中：xt和zt分别为t时刻的系统状态矢量和量测矢量；f(·)和h(·)分别为状态转移函数和观测函数；bt和vt分别为t时刻的过程噪声矢量和量测噪声矢量。

基于贝叶斯理论观点，状态估计问题是基于后验知识递归计算出当前时刻(t时刻)的状态后验分布p(xt|zi,i=1, 2,…,t)的。预测过程是利用先验分布p(xt|xt-1)预测系统模型的状态的，而更新过程中使用最新的量测量校正先验分布，从而得到后验分布。首先，假设系统的状态转移服从一阶马尔科夫模型，即当前时刻的状态xt仅与t-1时刻的状态xt-1相关。根据贝叶斯公式，可以推导出式(2)为预测，式(3)为更新[19]。

p(xt|zi,i=1,2,…,t-1)=

(2)

p(xt|zi,i=1,2,…,t)=

(3)

式中：p(zt|xt)为t时刻给定x的数据后的似然函数。

对于一般的非线性或非高斯系统，很难从上式中获得后验分布的解。因此，引入蒙特卡罗采样来解决这一问题。PF将后验分布近似为一组随机采样的粒子及其相关权重的集合，并且将计算出的数学期望作为状态估计。序列重要性重采样(sequential importance resampling，SIR)通常用于PF算法中，以克服PF的退化问题。根据文献[19]，后验分布可以通过狄拉克混合近似技术近似表示为

(4)

式中：δ为狄拉克函数；N为粒子数；wt,i为t时刻第i个粒子的重要性权值；xt,i为t时刻第i个粒子的状态。引入重要性分布函数q(xt,i|xt-1,i,zt)，则重要性权值可以表示为

(5)

(6)

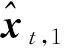
1.2 模糊量测更新

在量测更新阶段之后，如果估计量测值与真实状态量测值在相同条件下存在模糊点，则粒子协方差会增加。这种现象通常发生在式(1)中非线性函数h(xt)的拐点附近[22]。因为拐点附近的函数值在另一侧具有相同的对应值，所以量测更新可能导致分散的后验分布。

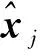
根据量测模型的形状和误差统计可知，如果量测模型在拐点附近更陡或具有更小的误差方差，则图4中的离散后验分布具有更明显的多模态分布。PF中的多模态分布可以使用混合表示法来处理，其中多模态分布占用的比例较大。Cramer-Rao界理论[23]表明：因为量测对Fisher信息矩阵是半正定的，所以协方差的下界不会因量测更新而增加；只有当量测模型的观测函数h(x)的梯度为零时，量测才为零，此时最优滤波的后验协方差小于或等于先验协方差。在估计状态时并没有较好地结合来自量测的附加信息，为得到最优滤波器，最好利用模糊度来求取真实状态信息。本文将模糊量测更新定义为导致粒子协方差增加的量测更新。模糊量测更新会引起较严重的粒子分散，因此估计的可信度较低，并且可能会对递归滤波器的后续步骤造成连锁效应。因此，提出基于无序量测的模糊更新来解决此问题。

2 基于无序量测的模糊更新

根据上文分析可知，模糊量测更新会导致分散的后验分布以及不可靠的位置估计。本算法的目的是，当发生模糊量测更新时，获得更优的当前估计置信度，从而获得更好的滤波性能。该算法的核心思想是，在先验分布适合量测更新的条件下，保存模糊量测并后续使用，本质上等同于量测到达延迟的情况。图5给出了延迟量测超时序列的量测关系。量测zt-1对应于t-1时刻的系统状态xt-1。假设t-1时刻zt-1的量测更新是模糊的，在zt的量测更新之后该滤波器使用zt-1，如同zt-1正好在t时刻zt之后到达。

以SIR-PF算法为基础，提出无序量测算法：

(7)

其中

(8)

式中：Qa,b表示从a时刻到b时刻的协方差矩阵；Ft,a和Qt,a分别表示从a时刻到t时刻的状态转移矩阵和相应的协方差矩阵；Fa,s和Qa,s分别表示从a时刻到s时刻的状态转移矩阵和相应的协方差矩阵；u为一个白噪声向量。新的重要性权重表示为ωr,i(i=1,2，…,N)(r≤t，其中r为正整数)，此权重是通过当前粒子状态值和非归一化权重计算得到的，其中包含当前的量测zt。根据新的权重对产生的粒子进行重采样，以获得包含无序量测信息的粒子状态值xr,i(i=1,2，…,N)。

(3)根据式(5)计算权重，并归一化权重。

(4)计算累积分布函数的协方差。

在初始化滤波后，以离散时间形式迭代地执行SIR。如果后验粒子协方差矩阵的行列式|st,2|大于相应的先验粒子协方差矩阵的行列式|st,1|，则认为更新是一个模糊量测更新，将先验粒子作为时间步长的解，即只执行预测步骤。如果更新被认为是模糊的，则跳过量测更新，跳过的量测值存储在集合A中；否则，认为此更新为一个正确的更新，并且检测集合A是否为空。如果集合A非空，则执行无序量测，并按先进先出的顺序利用每个量测值。在无序量测模糊量测更新之后，为了生成xr,i需要权重被重采样。如果新获得粒子的协方差矩阵的行列式小于当前的后验粒子的协方差矩阵的行列式|st,2|，算法以xr,i作为解。而后，将上一次成功更新的粒子状态值xt,i(i=1,2，…,N)存储到xs,i(i=1,2，…,N)中，用作无序量测的输入。与标准PF算法相比，该算法需要额外的计算来处理模糊量测更新，并且通过比较先验密度和后验密度的大小来确定模糊量测更新，后验协方差可以在量测更新之后求取。

3 实船实验结果分析

在GPS失锁期间，利用无人船上的测深仪给出海底深度测量值，并将其与电子海图显示与信息系统数据进行比较，以估计出无人船的位置。如图6所示，船舶测深仪是通过测量超声波信号自水底反射至接收的时间间隔来确定水深的一种仪器设备，测深仪提供的深度量测模型为

zt=h(xt)+vt

(9)

式中：xt表示无人船位置，是一个由经纬度表示的二维向量；h(xt)表示在xt处估计的深度量测信息；vt表示附加的量测噪声。无人船运动模型由马尔科夫过程建模：

xt+1=xt+ut+bt

(10)

式中：ut和bt分别表示相对运动信息和附加的过程噪声。船舶的相对运动信息由惯性导航系统(inertial navigation system，INS)估计。

图6 无人船测深原理示意图

实验中，无人船以5 kn的速度沿着图7所示的路径航行，船舶在凌水港附近航行约1 500 s。船舶配备的测深仪、INS等设备的参数见表1。测深仪设定为每隔1 s给出1次深度信息。

图7 船舶航行路径

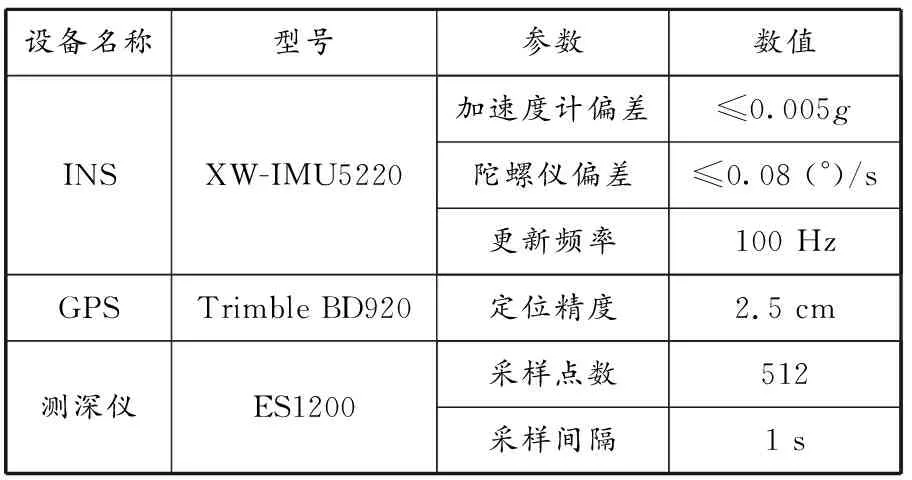
表1 实验用设备参数

在相同条件下分别对EKF[6]、PF[8]、MPF[19]和OOSMPF进行比较分析。3种基于PF的算法都是基于1 000个粒子的SIR框架实现的。对于每一种方法，都进行了100次蒙特卡罗模拟，得到了均方根误差(root mean square error，RMSE)和估计误差协方差的平均值。每个时间步长的RMSE由下式计算：

(11)

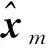
(12)

实验过程中对各种误差统计进行了测试，表2给出了各种标准差下不同场景的统计表，其中：过程噪声和量测噪声分别从标准差为σb和σv的高斯分布中采样；INS的偏差从标准差为σu的高斯分布中采样，在不同场景下保持不变，0.4 m相当于船用级INS允许范围内的位置漂移。

表2 各种标准差下的不同场景统计 m

场景1为过程噪声相对较小的情况。图8给出了场景1下基于时间的各滤波算法的RMSE曲线，图9给出了场景1下基于时间的协方差曲线。表3给出了0～1 500 s内所有算法的平均RMSE。在过程噪声较小的情况下，PF、MPF和OOSMPF的RMSE没有明显的区别，只是OOSMPF的结果略优于其他算法。然而，EKF具有更小的协方差，这是因为基于卡尔曼滤波的线性化量测模型未能逼近周围包含很多拐点的地形。因此，EKF提供了退化的状态估计。与EKF相比，3种PF的算法的协方差较大，这是因为先验密度覆盖的地形轮廓具有较少的量测更新。

图8 场景1下不同算法的RMSE曲线

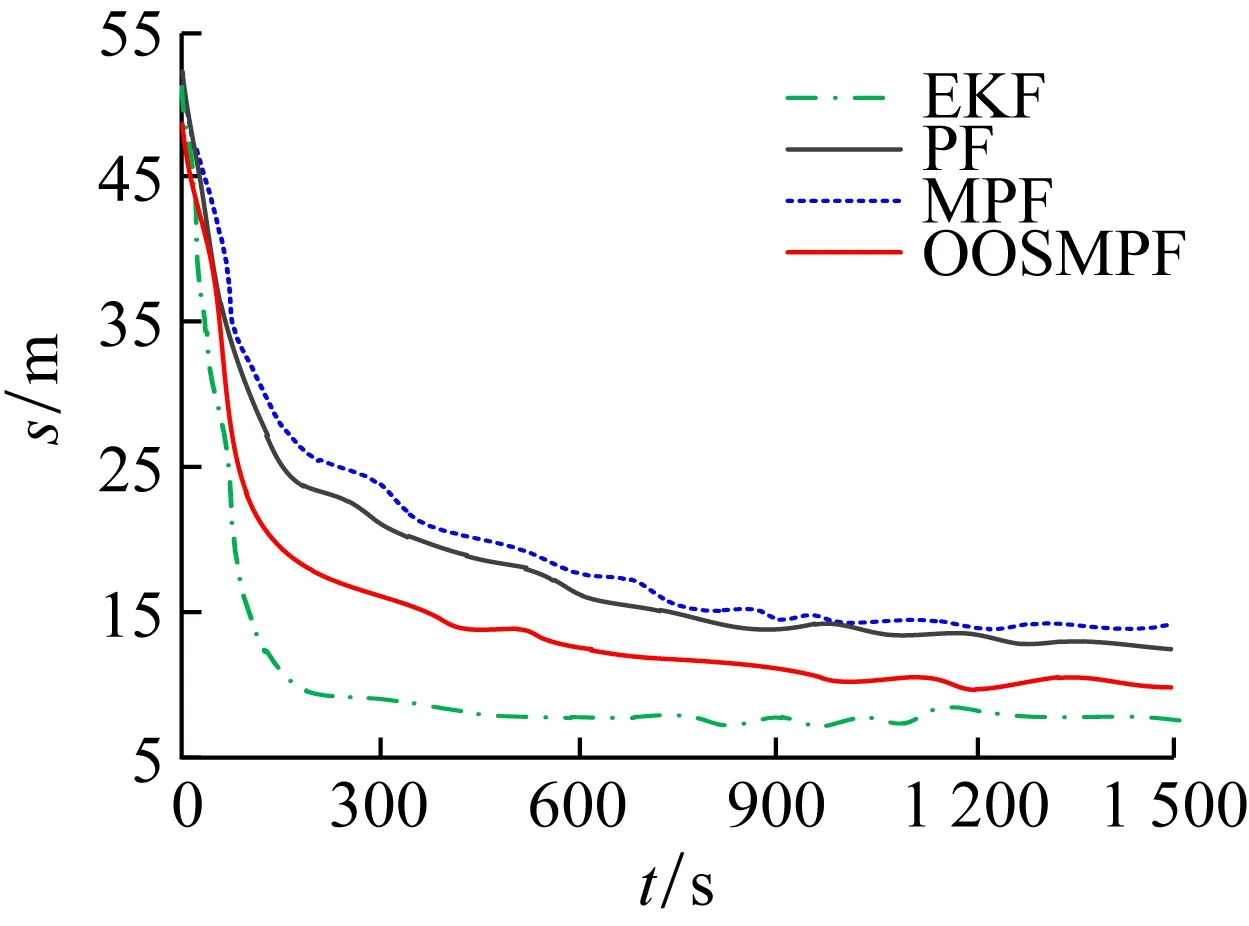
图9 场景1下不同算法的协方差曲线

场景2为过程噪声相对较大的情况。图10和11分别给出了基于时间的RMSE和协方差曲线。在所有的滤波算法中，OOSMPF的滤波性能最好。

表3 不同滤波算法RMSE的平均值 m

如表3所示，EKF的平均RMSE并不大，但模型的非线性导致滤波器不太稳定。当PF算法的协方差更小时，其性能下降(主要是因为不能很好地表征先验分布)，因此，在这种情况下使用PF会导致性能较差。OOSMPF成功地处理了模糊的量测量，并提供了更可靠、准确的状态估计。就RMSE和协方差而言，MPF在所有情况下都表现出与PF相似的特点，这是因为由于局部模糊性，偶尔会发生模糊量测更新。

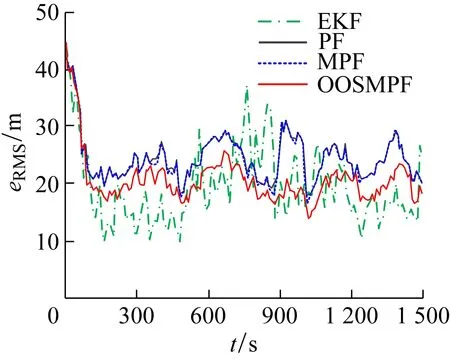
图10 场景2下不同算法的RMSE曲线

图11 场景2下不同算法的协方差曲线

场景3为过程模型和量测模型存在偏差并且过程噪声较大的情况。图12和13分别给出了基于时间的RMSE和协方差曲线。EKF的结果往往取决于其先前的轨迹，早期轨迹中大的误差对后续时间步长移动窗口中的预测阶段有不利影响。运行100次可以观察到1次轨迹发散，在这种情况下，窗口大小为1的EKF的轨迹发散得更加频繁，而PF呈现出较强的鲁棒性，OOSMPF的滤波性能最好，而且OOSMPF提供了比PF和MPF更可靠的估计值。

图12 场景3下不同算法的RMSE曲线

图13 场景3下不同算法的协方差曲线

4 结 论

本文设计了一种基于无序量测的粒子滤波算法处理模糊的量测更新，进而解决滤波器退化的问题。由于导致离散后验分布的模糊量测更新受到先验分布的影响，本文将模糊量测更新定义为导致粒子协方差增加的量测更新，并通过重塑先验分布来控制粒子的协方差。在SIR-PF的框架下，当先验分布足以用于量测更新时，针对无序量测问题利用模糊量测给出一个优化解。在无人船框架下对滤波结果进行了实船验证。与EKF、PF以及MPF等其他算法相比，本文设计的算法取得了更好的位置估计均方根误差性能。