基于Speedgoat的半主动悬架模糊PID控制研究
2023-01-02姚行艳胡力月
姚行艳, 胡力月
(重庆工商大学 检测控制集成系统重庆市工程实验室,重庆 400067)
0 引 言
汽车的悬架系统可以有效减少汽车行驶时的颠簸、冲击,增加乘客乘坐舒适性。因为被动悬架具有不可控制弹簧和固定的参数的阻尼器,只适用于特定工况,主动悬架则克服了问题可适应各种工况但是主动悬架通常需要较大的电流。半主动悬架结合了两者的优点既能有效规避被动悬架系统刚度,阻尼不变的弊端,还能取得与主动悬架系统相媲美的控制性能,而且其结构简单、能耗低、易实现,因此成为汽车悬架领域中的研究热点之一[1-3]。
要充分发挥半主动悬架系统的性能,需要合适的控制策略。庞辉等[9]提出将神经网络和粒子群优化相结合设计了一种变域模糊控制方案。Yang等[10]在提出新型半主动悬架系统模型基础上,提出了一种基于MPC控制策略的两级递阶控制方案但未将系统的可靠性和稳定性考虑在内。模糊控制是将相关领域的专家经验或知识用自然语言表达形成控制决策表,它不需要建立精准的数学模型、鲁棒性强,其具备勿需构建准确的数学系统、鲁棒性突出等优势。但若模糊控制域和隶属度函数划分不当会影响控制结果的准确性以及对系统稳定效果造成干扰,PID控制器积分模块能够有效地消除误差提高,微分模块可以提高系统的稳定性[2],模糊PID控制结合两者的优点根据系统误差的变化实时对参数进行调整可以实现在线对被控对象的有效控制。结合车辆二自由度1/4半主动悬架系统的动力学模型以及Speedgoat开发了一款半主动悬架模糊PID控制器,利用Speedgoat进行了半实物仿真试验,同时和应用被动悬架与经典PID控制的半主动悬架运行效果展开对比研究。
1 半主动悬架系统数学模型
1.1 车辆二自由度1/4动力学模型
为了更好地对汽车悬架系统进行研究,需要建立一个理想的动力学模型。对汽车模型进行性能研究时,越精简的模型涉及的参量越少,也更便于控制。二自由度1/4动力学模型结构简单但保留能体系了汽车在行驶中性能的参数因此本文对整车模型做出如下假设:簧上质量和簧下质量均视为刚体,忽略各组件之间的摩擦;车辆左右轮胎所遇到的路面激励一样,汽车无侧倾和横摆运动;车身相对地面只做z轴方向上运动。
根据上述的假设,可以将复杂的半主动悬架系统简化成如图1所示的动力学模型。表1列出了与悬架运动特征相关的一些系统参数值。
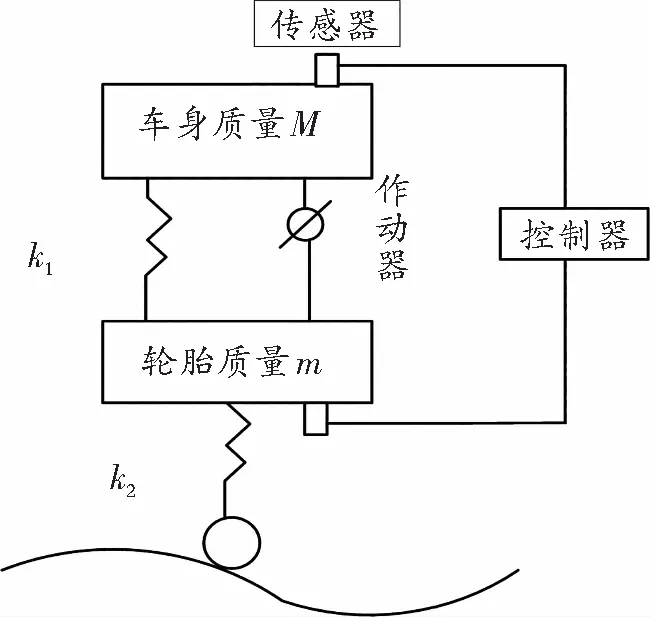
图1 半主动悬架系统动力学模型

表1 车身模型主要参数
1.2 随机路面输入模型
路面输入模型是分析受控车辆系统性能的重要基础之一,合适的路面输入模型能提高整个系统仿真结果的准确性。为了更好地模拟汽车在行驶时所受到的路面激励情况,采用滤波白噪声作为路面模型的输入。
(1)
其中,x0(t)、f0、GP(n0)、u、w(t)分别指代里层不平度移动;下截止频率,即0.1;路面的不定度指标;车速以及均值是零的高斯白噪声。
1.3 汽车半主动悬架系统数学模型
根据半主动悬架系统的运动特性,由半主动悬架系统动力系统,构建了图1的数学系统。
结合牛顿第二定律,可获得二自由度1/4半主动悬架动力学方程即:
(2)
(3)

图2 半主动悬架数学模型
整理可得:
(4)
(5)
其中,fx为为阻尼力。根据式(2)和式(3)将系统运动方程表示为系统的状态空间方程,如下所示:

(6)
y(t)=Cx(t)+Du(t)
(7)
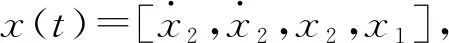
(8)
2 半主动悬架系统模糊PID控制
2.1 汽车半主动悬架模糊PID控制
模糊PID控制实际上就是将模糊算法应用到PID参数的选择上,本文选择二维输入的模糊控制器,将车身在Z轴加速度偏差e以及加速度的偏差变化率ec当作模糊控制器的输入。为了达到更好的控制效果,模糊控制器输出的PID参数会时刻随着输入的变化而改变。
(9)
其中,KP0、KI0、KD0是经典PID控制模块的t=0时刻的值,KP、KI、KD则是模糊PID控制组件的输出值。
想要得到最终的PID控制参数,要经历以下3个步骤:第一先将精确的输入量通过隶属度函数模糊化得到模糊子集;第二步根据采集到的模糊输入计算出相应的隶属度然后在控制规则中找到输出值的隶属度;第三步将得到模糊化输出通过隶属度函数结模糊化得到精确的输出参数。将初始时刻的PID参数与输出的参数相加即为模糊控制PID的输出量。
2.2 半主动悬架模糊PID控制器设计
输入以及输出参量的模糊论域都为[-3,-2,-1, 0, 1, 2, 3]划定成7个语言参量,分别是负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)。由此获得Kp、Ki、Kd的模糊控制机制,如表2。
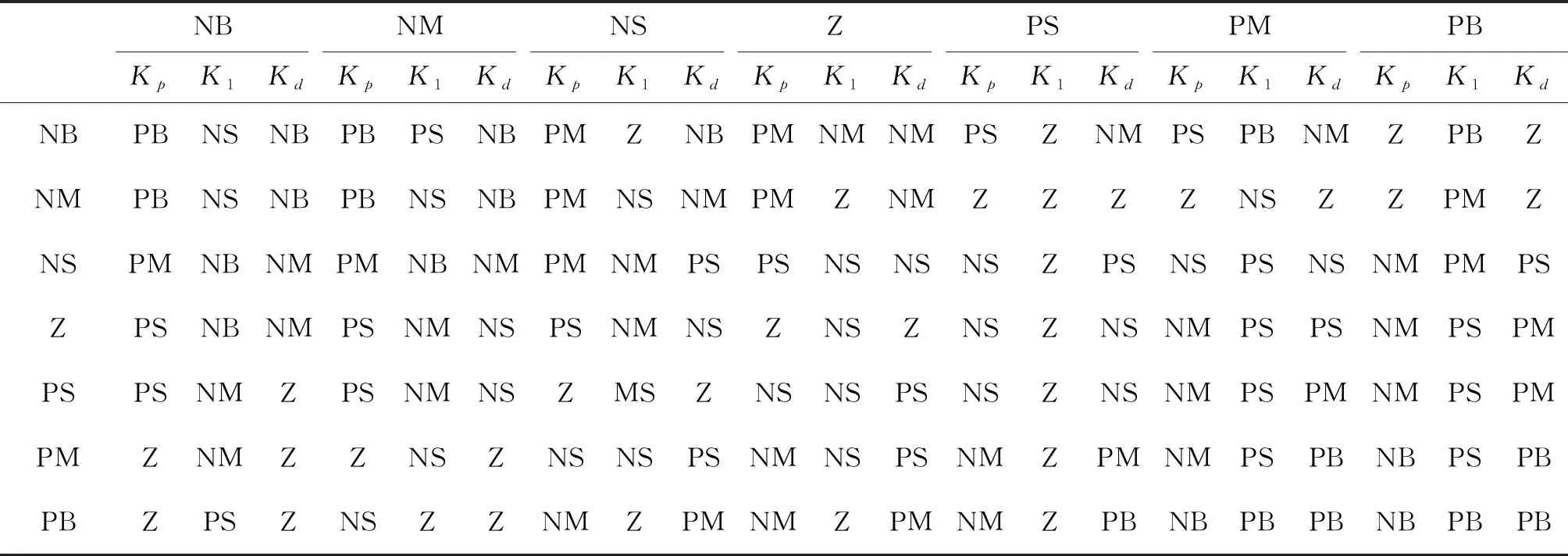
表2 模糊控制规则
明确这一模糊器的模糊化因子,即ke、kec分别为1和0.2;解模糊化因子为K1、K2、K3分别为0.2、1、1。
确定高斯方程为输入方程的隶属函数。三角形函数为输出变量的隶属函数。解模糊的方法是面积重心法[7]。模糊控制的制定规则即:当偏差出现过高情况下主要以提升KP、KI的值尽快消除偏差为目的;如若误差不大的情况下,可适当减小KP、KI从而避免系统超调,提升稳定效果。
3 半主动悬架系统硬件设计及实现
基于Speedgoat的半实物仿真与Matlab/Simulink可以实现无缝连接。采用车身加速度作为输出信号控制对象,以尽可能降低车身加速度为目的来建立模糊PID控制系统。
Speedgoat输出加速度信号经过IO102板卡传输到功率放大器并控制激振器振动,从而模拟车身加速度的上下振动,振动信号通过加速度传感器输入到示波器中,示波器就能实时显示加速度波形并能采集到经激振器仿真的数据。所搭建的实验平台如图3所示。

图3 Speedgoat仿真实验平台
在Matlab/Simulink模拟环境下,以Speedgoat为基础搭建的半主动悬架系统模糊PID控制的模拟模型框图如图4所示。
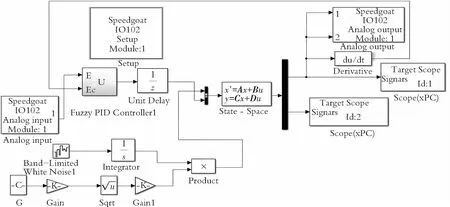
图4 半主动悬架模糊PID控制模型框图
4 半实物仿真结果与分析
结合Matlab/Simulink以及Speedgoat对半主动悬架系统予以半实物模型,同时把模拟的结果和应用被动悬架,经典的PID管控的半主动悬架模拟结果予以对比。
假定车辆于B级路面情况下,按照20 km/h、40 km/h、60 km/h的速率运行,在此种情况下,被动悬架模型、PID控制模型和模糊PID控制模型的车身垂向速度分别如图5所示。

(a) 20 km/h (b) 40 km/h (c) 60 km/h
同理,假定汽车在C、D、E级路面输入下以20 km/h、40 km/h、60 km/h的速度行驶,在此种情况下,被动悬架模型、PID控制模型和模糊PID控制模型的车身垂向加速度分别如图6、图7、图8所示。

(a)20 km/h (b) 40 km/h (c) 60 km/h

(a) 20 km/h (b) 40 km/h (c) 60 km/h

(a) 20 km/h (b) 40 km/h (c) 60 km/h
从图6—图8中可知,在不同路面等级、不同速率情况下,在模糊PID控制策略下和经典的PID控制策略下的半主动悬架系统的垂向加速度与相同控制策略下的被动悬架相比要小得多,其中模糊PID控制下的加速度减小得更多,控制效果更为理想。表明了设计的模糊PID算法可以更为理想地保证车子的平稳运行,提升车的乘用舒适度。
为更好地论证模糊PID算法下的半主动悬架表现,结合车身的垂向加速度均方值为评估参量,对比分析在不同等级路面输入下模糊PID控制相较于经典PID控制和被动控制的有效性,其结果如表3所示。
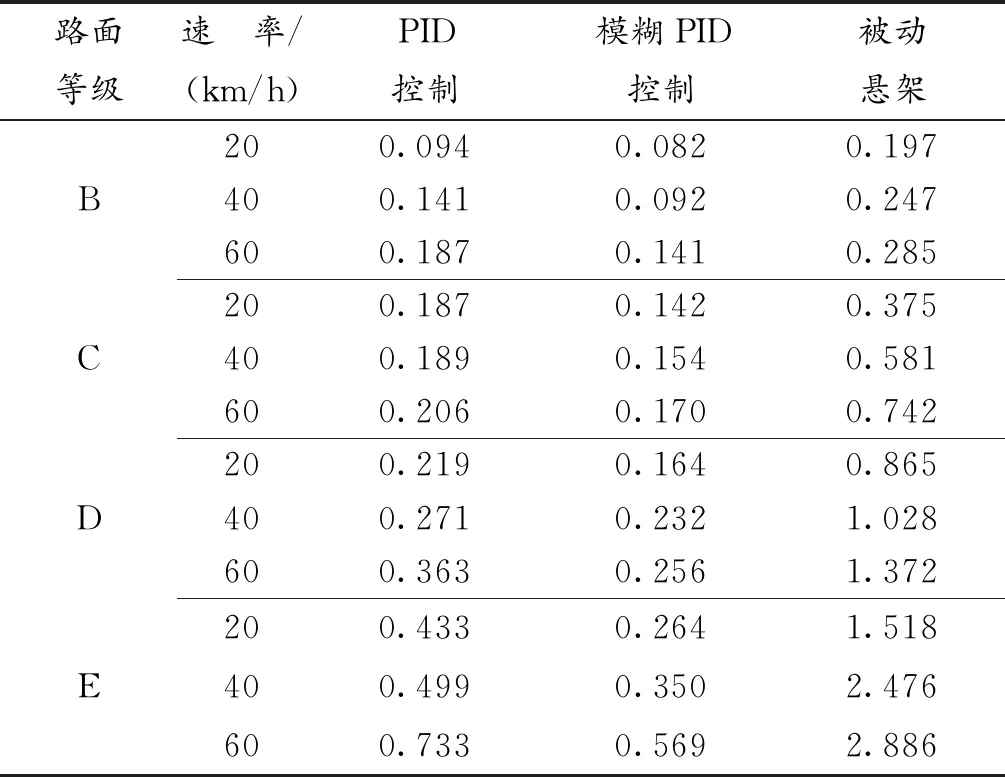
表3 仿真结果均方根值对比
仿真结果表明:在不同路面等级、不同速率情况下选择模糊PID以及经典PID两类控制算法的半主动悬架系统垂向加速度均方值都比选择被动悬架下的值有明显下降,而采用模糊PID控制下的垂向加速度均方根值降低幅度更大。当车速为20 km/h时,在B、C、D、E级路面输入下,模糊PID算法对比于被动悬架垂向加速度均方值结果依次降低了41.7%、37.9%、19.0%、17.4%。当车速为40 km/h时,在B、C、D、E级路面输入下,模糊PID控制相较于被动悬架垂向加速度均方根值分别减少了37.3%、26.6%、22.6%、14.1%。当车速为60 km/h时,在B、C、D、E级路面输入下,模糊PID控制相较于被动悬架垂向加速度均方根值分别减少了49.6%、23.0%、18.7%、19.7%。
5 结 论
采用鲁棒性较强的模糊PID控制策略,搭建了汽车二自由度1/4主动悬架系统,引入Speedgoat予以半实物模拟,最终可得以结合了Speedgoat的半主动悬架模糊PID控制器,在不同条件下都能有效降低整车的垂向加速度,且优于经典PID控制。由此说明,所设计的基于Speedgoat的半主动悬架模糊PID控制机制有着突出的操控性,大大提升了车辆运行的稳定性以及舒适度。
