基于因子分析的因果推断研究
2023-01-02付举望孔新兵
付举望, 孔新兵
(南京审计大学 统计与数据科学学院,南京 211815)
0 引 言
统计学中,相关关系能够通过相关系数进行度量,而因果关系却很难有一个明确的度量指标,由此衍生出的因果推断(Causal Inference)问题成为统计学者们关注的焦点。Rubin[1]在反事实理论基础上构建了潜在结果模型(Rubin Causal Model),其核心是比较同一个研究对象在接受干预和不接受干预时的结果差异,即该干预的因果效应(Causal Effects)。在该反事实框架下,因果推断问题转变为反事实值的估计问题。目前,关于受数据限制较小,能够服务于高维数据,且估计效果更好的因果推断方法,还有待进一步研究。
Rubin关注单个协变量情形下平均处理效应的估计问题,通过处理组与控制组的分离与再匹配估计反事实值; Heckman等[2-3]使用双重差分法(Difference-in-Difference) 估计反事实值,并将其应用于社会公共政策评估;Abadie 等[4]提出合成控制法(Synthetic Control Method),将控制组个体加权,合成一个与处理组相似的虚拟组,通过比较干预前后的处理组和虚拟组的变量变化,得出平均处理效应, 改进了双重差分法的内生性问题;Zheng 等[5]又在此基础上,使用机器学习二次规划法来确定控制组的权重并重构虚拟组,以预测反事实值;Doudchenko 等[6]比较了双重差分法、合成控制法、约束回归法、最优子集选择法对于估计参数的不同限制条件,并使用弹性网法(Elastic Net)设置惩罚项,以此筛选控制变量构造模型,获得反事实值预测。这些方法都是基于观测到的面板数据特点进行模型假设,导致其受限于所得观测数据,在面对具有不同特征的数据时稳健性较弱。
因子分析作为常见的宏观经济变量预测方法,面对高维数据表现优异且能应用于不同特征的数据。因此在反事实框架下,学者们通过非随机观测数据,在因子分析的视角下进行因果推断,提出了新的反事实值估计方法。Xiong 等[7]提出带有缺失值情况下的潜在因子模型,其通过行列调整后的协方差矩阵估计获得公共因子与因子载荷,由此得到反事实值估计;Bai 等[8]提出TW算法(Tall-Wide algorithm),其假设面板数据具有强因子结构,并将数据划分为bal、tall、wide、miss 4块(block),分别利用tall-block 估计公共因子、wide-block估计旋转后的因子载荷,从而得到平均处理效应的估计。这些方法都是在因子分析前对面板数据进行调整,将缺失值所在行、列或是周围一整块数据丢弃,导致已有观测数据信息无法完全利用。
本文从优化的角度提出L2因子分析方法,获得平均处理效应估计,且避免了信息丢失问题。与Xiong 等不同,该优化方法的显著优势在于勿需调整面板数据的行和列,也勿需为了构造满足奇异值分解的子矩阵而整行或整列地丢弃数据;而与Bai等的区别在于:该优化方法将除缺失值以外的所有数据作为整体进行因子分析,而非将整个面板数据划分后根据特定数据块分别进行潜在因子与因子载荷估计,勿需舍弃未使用数据块的信息。该方法仅需舍弃面板中的缺失值,即可通过优化一步得到潜在数据生成效应,即潜在结果,从而提高估计效率。另外,与上述文献关心平均处理效应不同,本文还通过引入L1损失函数并优化L1风险,得到中位数处理效应的估计。
1 处理效应模型
本文以政策评估为例,简述反事实框架与随机对照实验。假设某个城市(i)在某个时刻(t)被政策介入,在该地区对感兴趣的某项指标yI,t进行研究。考虑拥有关于该城市以及其他未被政策介入的城市的面板数据Y∈RN×T,其中在政策实施前的数据一共有a年,实施后的数据一共有b年,共计T年(T=a+b)。
借鉴已有因果模型变量设置方法,记城市i=1,2,…,n1为被政策介入的城市,作为实验组(treat unit);城市j=1,2,…,n2为未被政策介入的城市,作为控制组(control unit),共计N个城市(N=n1+n2)。时间t=T1,T2,…,Ta,Ta+1,…,Ta+b,其中t=T1,T2,…,Ta为介入前,t=Ta+1,Ta+2,…,Ta+b为介入后,将面板数据YN×T划分为4个部分,具体变量设置如表1所示。

表1 变量设置
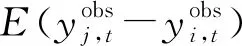
(1)
由式(1)可以看出:只需要多次进行实验估计反事实值,将其与真实观测值的差求期望即可得到政策的因果效应。Rubin(1973)提出了一般化的估计方法框架:
(2)
即实验组的值可以表示为控制组值的线性组合。由此一来,就可以通过对处理前实验组和控制组进行回归,得到参数ω=(ω1,ω2,…,ωn2)和μ,再使用估计出的参数和处理后控制组的值估计处理后实验组的反事实预测值。这样一来,问题就由求反事实估计值变为求回归估计参数θ=(μ,ω)。一个简单的想法是利用简单最小二乘法最小化以下目标函数Q0,来得到参数ω和μ的估计:
但当θ=(μ,ω)的维数较高时,最小二乘法将导致较大的预测误差,使得政策效应的估计变得非常不稳定。因此,在这基础上还需要一些假设条件对参数θ=(μ,ω)加以限制。而目前的各种方法,均是基于已有面板数据设立模型假设,在该假设下对参数θ=(μ,ω)施加条件,以获得更好的估计效果。
2 基于因子分析的反事实值估计
2.1 因子模型及其估计
近年来,因子模型的理论和应用已经得到了很大的完善和发展,动态因子模型常被应用于宏观经济政策的评估、经济指数的构建和经济指标的预测。统计学中,学者们关注因子个数的确定研究以及公共因子与因子载荷的估计方法研究。Bai[9]提出确定静态因子个数的信息准则,该准则在保证因子模型的拟合优度前提下,通过面板数据结构特征得到因子个数的无偏估计;Fan等[10]讨论具有条件稀疏结构的高维协方差估计问题,通过引入POET(Principal Orthogonal compl Ement Thresholding)方法来探索这种近似因子结构;Kong[11]提出一种局部主成分分析方法,用高频数据确定具有时变因子载荷的连续时间因子模型的公共因子数,该模型采用离散时间因子模型在收缩块上进行局部近似。

(3)
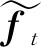
通常,一个数据集总是由若干随机变量的若干观测组成。因子分析的目标就是将原始数据集进行降维,将这些观测投射到一个低维因子空间中。这样的投射有无数种,主成分方法希望找到这样一种投射,可以使得数据在低维空间的投影拥有最大的方差。而L2因子分析问题则可以表述为目标函数Q1的最小化问题:
其中:Λ=(λ1,…,λn1,λn1+1,…,λN)T,F=(f1,…,fa,fa+1,…,fT)。对于目标函数Q1的最小化问题,常用方法为对协方差矩阵YTY进行奇异值分解(SVD),寻找最大的r个特征值,再用其对应的r个特征向量构成的矩阵做低维投影降维。
2.2 L2范数因子分析
在对带有大量缺失值的面板数据进行因子分析时,基于最小二乘法的经典方法会遇到稳健性问题,难以得到满意的公共因子与因子载荷。对于缺失值处理,Xiong 等提出带有缺失值情况下的潜在因子模型,在协方差矩阵估计时,对所有个体重加权,删除缺失值所在的行和列,从而将面板数据调整为满足奇异值分解的子矩阵,再根据所得矩阵的特征向量进行潜在因子与因子载荷的估计; Bai 等将面板数据划分为4块(block),分别利用tall-block 估计公共因子、wide-block 估计旋转后的因子载荷;而本文则从优化的角度直接舍弃目标函数中对应缺失的累加项,此时的目标函数Q2改写为
s.t.ΛTΛ/N=IN,FFT/T为对角阵。
使用该方法的优点是勿需对面板数据的行列进行拼凑和删减操作,且使用了所有未缺失数据的信息。
2.3 L1范数因子分析
L2因子分析的缺陷是对离群值十分敏感,为了解决该问题,本文使用更具有稳健性的L1因子分析进行研究。
将目标函数Q2更换为使用L1范数,即可得目标函数Q3:
s.t.ΛTΛ/N=IN,FFT/T为对角阵。
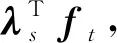
2.4 交替凸优化算法
目标函数Q1、Q2与Q3的最小化问题实质为无约束最优化问题。其中Q1为均值插补后的因子分析,可使用奇异值分解进行直接计算;Q2与Q3则需要使用优化算法解决。
一种经典的方法是使用交替凸优化算法求解该问题。该算法的思想是:当面临一个两维变量的优化问题,而该问题不是凸优化问题因此无法求其最优解时,可以采用交替迭代的方法,每一步将其中一维未知变量的值看作是常数(使用该变量上次迭代的取值),来求解另一维未知量。由目标函数Q2与Q3给出式(4)、式(5):
(4)
(5)
改写目标函数Q2与Q3,有
Q2(Λ,F)=‖Y-Λ(m-1)F‖L2=
Q3(Λ,F)=‖Y-Λ(m-1)F‖L1=

(6)
(7)
同理将式(5)转化为下面的N个独立的子优化问题:
(8)
(9)
其中:λs是Λ的第s行。式(6)—式(9)都可以采用线性规划问题求解。在带有缺失值的情况下,直接舍弃目标函数中的对应累加项,在上述算法中对应的做法就是直接删除一个约束条件。
需要注意的是,交替凸优化算法只能保证在每一步求得当前最优解,并不能保证最后得到全局最优解。具体算法步骤如下(以L2因子分析为例):
Step1 初始化参数:给出Λ、Σ的初始值Λ(0)、Σ(0)。
Step2 交替凸优化:对于迭代次数m(m=1,2,…,M),有
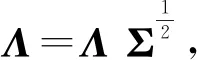
将算法中L2范数改为L1范数即为交替凸优化求解L1因子分析。关于初始值的选取,Σ为对角矩阵,使用单位矩阵作为初始值Σ(0);而Λ可以采用简单随机数进行初始化,这里为了加快收敛速度,使用均值插补后通过奇异值分解(SVD)算法得到的因子载荷矩阵作为初始值Λ(0)。
2.5 预测效果评价
由于反事实值永远无法得到真实的观测值,所以在随机对照实验中无法获得预测误差,从而无法比较各个方法的预测效果。常用的解决方法是Abadie提出的安慰剂检验法,其在因果研究中用于检验反事实估计量是否具有稳健性。安慰剂(placebo)源于医学上的随机实验。研究者为检验药物是否有效,将实验人群随机分为服用真药的实验组与服用安慰剂的控制组,通过不让实验者知道自己服用的是真药还是安慰剂,来避免主观心理作用的影响。以此为基础的安慰剂检验,其核心思想在于从控制组中选取伪实验组,并用相同的方法估计虚拟的“反事实值”,这样能同时获得真实的观测值与估计的预测值,即可对预测结果进行评价。由此得到的安慰剂效应(即真实值与虚拟反事实值之差)越趋于0,说明其与该政策的因果效应差距越大,也就说明估计方法越稳健。在实证研究中,安慰剂检验受到了广泛使用。Abadie通过假定控制组城市受到政策影响估计安慰剂效应,并作图比较,说明合成控制法的稳健性;Athey等[13]则分别假设虚拟实验组与虚拟政策实施时间,对双重差分、带惩罚项的横向递减法(horizontal regression)、矩阵补全方法(Matrix Completion Methods)等多种方法进行了比较。
本文具体考虑以下两种情况:
(1) 随机选取控制组城市j*,假设其在t=Ta+1,Ta+2,…,Ta+b时间段中受到政策介入影响,成为伪实验组(pseudo-treat unit)。其余控制组城市(j(.))仍然为控制组,政策介入时间不变。具体变量设置由表2所示。

表2 伪实验组假设
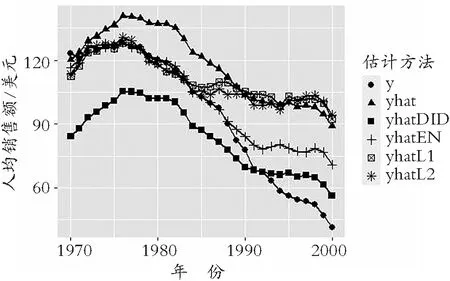
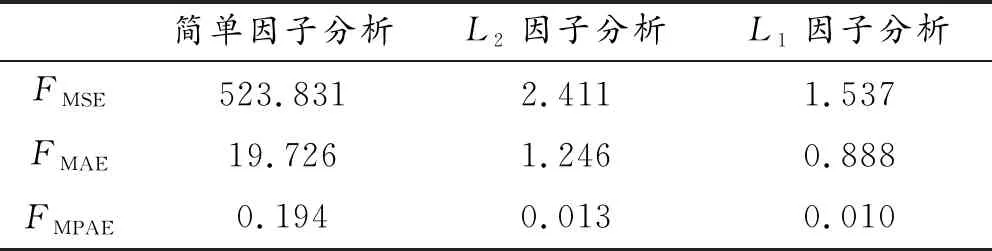
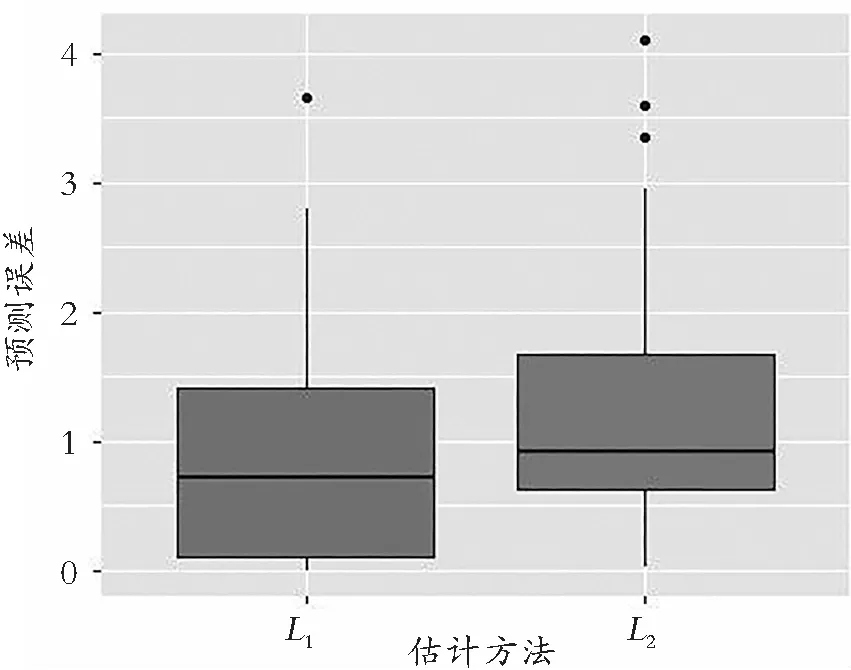
(2) 随机选取时刻Ta+c与Ta+d(其中Ta+c满足时间顺序Ta+1,Ta+2,…,Ta+c,…,Ta+d;1 表3 伪时间假设 在以上两种情形中,同样地将“介入后”的“实验组”数据视作缺失值,用上节的方法进行因子分析,并将得到的L1因子和L2因子以及对应因子载荷建立预测模型,预测“反事实值”。在安慰剂检验中,能同时获得真实的观测值与估计的预测值,对预测结果进行评价。下面选取3种指标:FMSE、FMAE和FMPAE,并由这3种指标比较各方法的预测精度。计算方法如式(10)所示(eit为实验组城市i在t时刻的预测误差): (10) 本文选取因果推断研究中部分学者使用的关于加利福尼亚州限制吸烟政策的数据(Abadie等,2010; Doudchenko等,2016; Athey等,2021)。使用该数据的优势在于:可以通过本文使用方法得出的结果与以往已有估计方法得到的结果进行比较,对因果效应是否存在进行基本验证。在该数据中,加利福尼亚州于1988年被限制吸烟政策介入,作为实验组;选取另外38个未被任何吸烟管控政策介入的州作为控制组。同时选取了1970—2000年共计31a间各州的烟草销量数据,并设定1988年为政策介入时刻(Ta),该政策于1989年(Ta+1)起对烟草销量产生因果效应。 实证研究中,面板数据Y为39行、31列的矩阵。在具体因子分析模型中,N=39,n1=1,n2=38;T=31,a=16,b=15。采用Bai等提出的信息准则确定静态因子个数。在该信息准则下,因子个数需要最小化: 其中,V(Λ,F)为因子残差平方和,G(N,T)为惩罚函数,其使得在N,T→∞时,G(N,T)→0,且min(N,T)G(N,T)→∞。参考Bai&Ng(2002)建议,本文在实证研究中选择式(11)作为惩罚函数: (11) 之后对目标函数Q2与Q3利用交替凸优化算法进行迭代,分别得到对应的潜在因子Ft与因子载荷Λs;再通过Ft与Λs进行估计,获得加州在没有被政策介入情况下的反事实预测值;最后由式(1)得到加州限制吸烟政策在不同方法下计算出的政策效应。 实证研究中,除了本文因子分析相关的3种方法外,使用因果推断中常见的双重差分法(Difference-in-Difference,DID)以及Doudchenko(2016)使用的弹性网络法(Elastic Networks)作为比较,由式(4)计算所得的政策效应(表4)。 表4 政策效应估计 表4给出了用不同方法得到的限制吸烟政策对于烟草价格的因果效应。可以看出政策效应均为正,且本文所使用的3种方法效应更显著。具体每年的预测值如图1所示。 图1 各方法每年预测值 其中,线y为加州烟草销售额的实际变化。由图1可以看出,双重差分法(线yhatDID)全时间段估计效果均较差,不能说明政策效应是否显著。经过均值插补后的简单因子分析(线yhat)虽然在1989年政策介入后的估计与实际值有显著差异,能够说明政策的因果效应,但在政策介入前的时间段(1970—1988)与实际值相差较大。而L1因子分析(线yhatL1)、L2因子分析(线yhatL2)以及弹性网络方法(线yhatEN)均能在政策介入前与实际值保持一致,且在介入后与实际值表现出显著差距。 伪实验组假设中,随机抽取5个原控制组州作为伪实验组,其余33个州仍为控制组。政策介入时刻、介入前后总时间不变,由式(10)计算所得误差如表5所示。 表5 伪实验组假设预测误差 由表5可以看出:通过均值插补后的简单因子分析得出的结果误差较大,而L1、L2因子分析的效果均不错,且L1范数较L2范数具有更小的平均预测误差。具体到每个伪实验组的平均预测误差,L1、L2因子分析所得的箱线图如图2所示。 图2 伪实验组假设预测误差 由图2可以看出:L1因子分析离群值点更少,最大值也更小,总体而言预测误差也小于L2因子分析,可以认为该情况下,L1范数预测效果略好于L2范数。 伪时间假设情况中,将1999年作为伪政策伪介入时刻(Ta+c),该政策于2000年(Ta+c+1)起对烟草销量产生因果效应。控制组与实验组不变,选取1989—2019年共计31a间各州的烟草销量数据,由式(10)计算所得误差如表6所示。 表6 伪时间假设预测误差 由表6可以看出:通过均值插补后的简单因子分析得出的结果误差较大,而L1、L2因子分析的效果均不错,且L1范数与伪实验组假设一样具有更小的预测误差。具体到实验组每年的预测误差,L1、L2因子分析所得的箱线图如图3所示。 图3 伪时间假设预测误差 由图3可以看出:L1因子分析离群值点情况与L2因子分析相差无几,而总体预测误差明显小于L2因子分析,可以认为该情况下L1范数预测效果同样好于L2范数。综上所述,经均值插补后的简单因子分析表现较差,各个误差显著大于另外两种方法。而L1、L2因子分析的预测效果在不同情况下表现优秀,且L1因子分析在两种假设下效果均略好于L2因子分析。通过比较,可以认为L2因子分析在进行因果推断时,虽然具有一定稳健性,但较之于L1因子分析仍有所欠缺。 首先简要介绍了因果推断的提出与发展历程。通过已有文献,概述了因果推断的相关模型,确定其最终目的是反事实值估计,并介绍了已有的估计反事实值的方法与理论模型;之后引入因子模型的基础理论,包括基本概念和模型参数的估计方法:正交因子模型主要通过主成分分析法来估计,而主成分估计得出的因子得分可以很好地应用于宏观经济变量预测;由此,结合因果推断与正交因子模型,将因果推断反事实值估计转变为带有缺失值的潜在因子模型估计。 基于以上理论依据,舍弃面板数据中的缺失值,通过优化一步得到潜在结果与平均处理效应;并采用L1因子分析代替L2因子分析来估计模型,做出稳健性上的改进,获得中位数处理效应;通过对L1因子分析的问题进行表述,介绍了一种交替凸优化算法并给出其实现步骤。 最后,为了验证L1因子分析能否代替L2因子分析作为因子模型的估计,基于加利福尼亚州限制烟草政策案例作了实证研究,将两种不同的主成分估计应用在反事实值的预测上。实证研究的结果表明:因子模型的L1估计量同样适用于宏观经济变量预测。后又通过伪实验组与伪介入的假设,分析比较了L1、L2因子分析的预测效果,结果表明L1因子分析较之其他方法具有更稳健的预测效果。
3 实证分析
3.1 数据选取与变量设置
3.2 模型设置
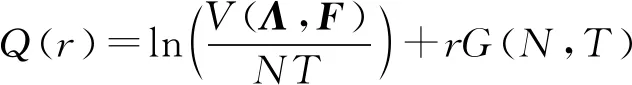
3.3 预测结果分析

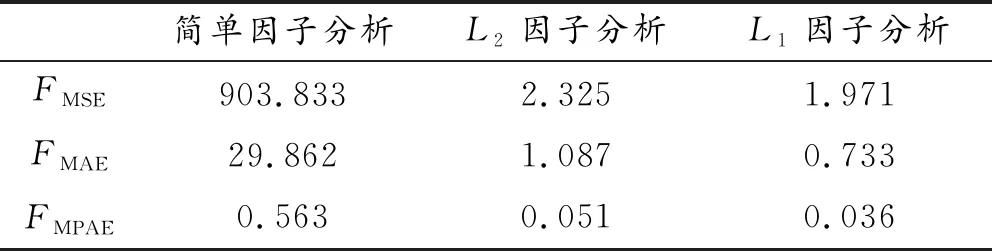
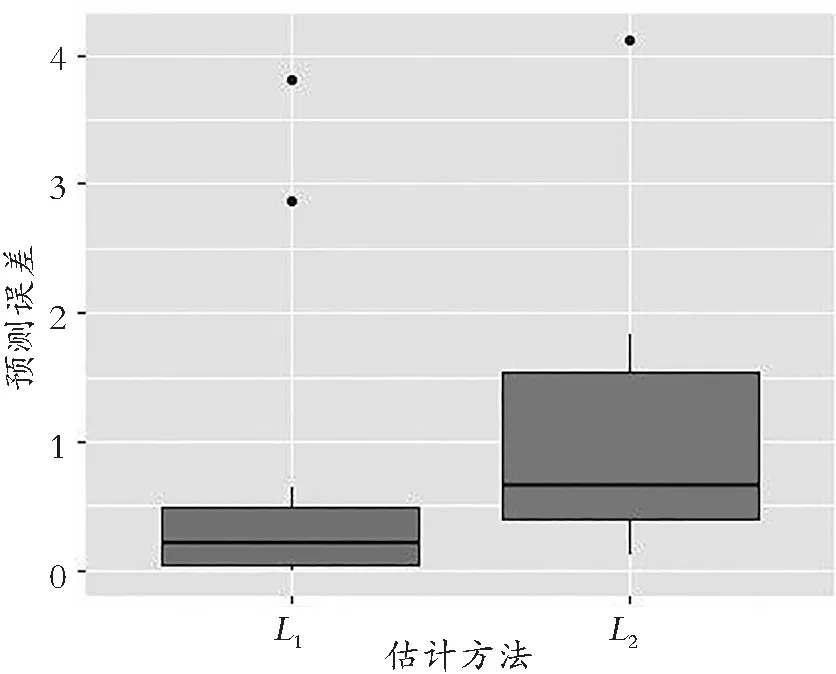
3.4 预测误差分析
4 总 结
