一种带有灾难和伯努利机制的M/M/1队列
2023-01-02刘力维闫俊娜
陈 潜, 刘力维, 闫俊娜
(1. 南京理工大学 理学院,南京 210094;2. 安阳学院 数理学院,河南 安阳 455000)
0 引 言
日常生活中到处都可看见队列的身影,小到面包店,大到火车站、飞机场,排队模型都发挥着不可或缺的作用。现今,工业、互联网、通讯、高新科技等发展迅速,灾难类排队模型的应用也越发普及。系统的运行不是一帆风顺的,灾难发生会使系统失去工作能力,所有顾客从系统中永远离开。Yang等[1]考虑一个带有清除机制的系统,首次将清除机制命名为“灾难”,求出系统队长的分布;Sudhesh等[2]在文献[1]的基础上研究了一类具有系统灾难的离散时间G/G/1队列,导出系统中顾客人数的瞬态概率和稳态概率。文献[1,2]对于灾难类排队模型的发展和应用起到了重要作用,但是对于系统发生灾难后需要维修的情况考虑不全面。
灾难的发生意味着系统需要被维修。Economou等[3]研究了一个可修的M/M/1队列,文中工作台发生故障勿需等待就会得到维修,维修后会恢复其工作能力,使得维修在排队模型中被广泛研究。实际情况下,修理工到达后才可维修系统,即延迟维修;Yu等[4]在文献[3]的基础上考虑带有延迟维修的M/M/1队列,证明了稳态存在的充要条件,使得维修状态更加贴合实际;Rao等[5]研究两阶段马尔可夫延迟维修排队模型,服务器在服务的任何阶段均可能出现故障,求出系统不同状态下队列长度的均值和损失率,扩充故障和延迟维修在系统中的范围。但上述文献对于工作人员休假情况研究不深入。
系统的工作必须由人指挥,注定需要安排工作人员休息。Keilson等[6]引入Bernoulli GI/G/1休假模型,证明穷举服务的分解结果可扩展到伯努利休假模型中;Arivudainambi等[7]研究了带有伯努利休假的重试队列,给出稳态的充要条件,在模型求解过程中借用辅助变量法,使得模型求解更加便捷;徐金萍等[8]研究了带有伯努利休假的M/M/1队列,借助拟生灭理论,得出相关的概率表达式,为休假模型中拟生灭理论的应用作出了推广。
工作人员出错或系统卡顿会使当前的服务出现问题,这时就需要反馈机制发挥作用。反馈指顾客经过一次服务后没有离去,而是回到队首等待下次服务。潘致锋等[9]分析一个带有伯努利反馈机制的队列,借助马氏链方法,求解了稳态下系统中顾客数的表达式,给出了逗留时间的LST(拉普拉斯变换),推广了马氏链的应用;Bouchentouf等[10]分析一个伯努利反馈队列,导出了工作台处于忙期时系统队长的显式表达式;Shweta[11]研究离散时间下带有反馈的队列,使用生成函数法求出了系统和重试轨道的队列长度;Ye等[12]在文献[1,3,6]的基础上研究了伯努利休假下具有灾难和维修的单服务台队列,求出了稳态队长的分布和一些性能指标,但模型仍然不够完善,还需补充。
综上所述,为了使带有灾难的排队模型更加完善贴合现实;本文在带有灾难和伯努利机制的队列中加入了延迟维修和反馈状态;利用马氏链方法和强马尔可夫性,求出相应的性能指标,使其具有更广泛的意义和应用价值。
1 模型描述
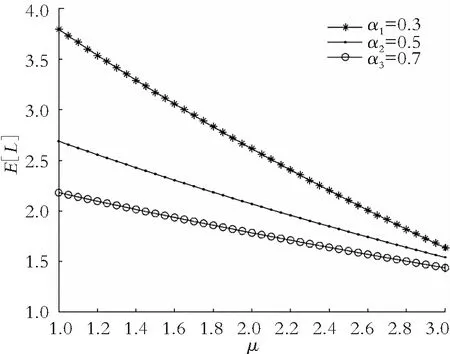
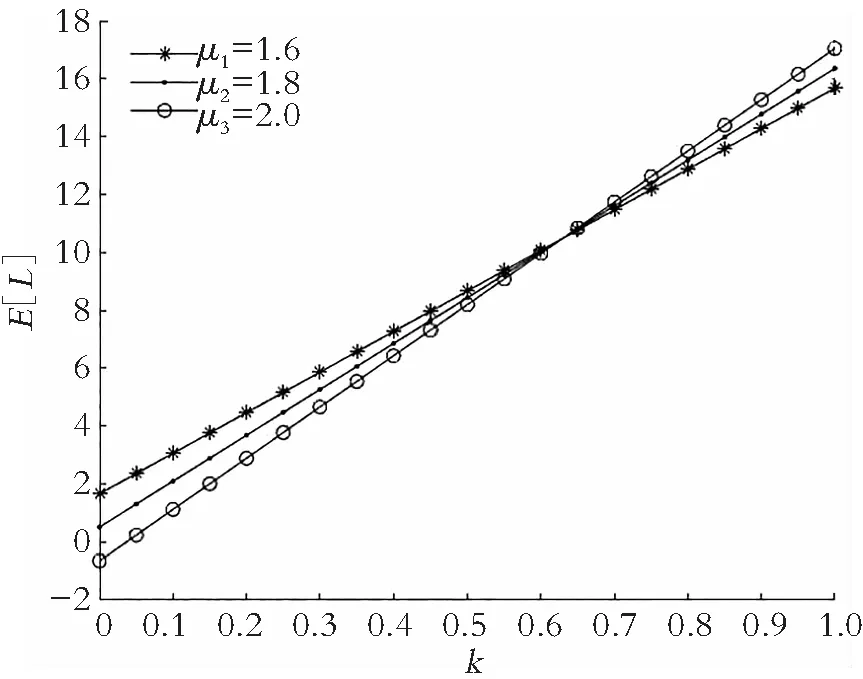
研究一个伯努利机制下具有灾难、延迟维修、反馈和休假的M/M/1队列。顾客按强度为λ的泊松流到达,工作人员对系统最前端的顾客完成一次服务时,休假的概率为q(0 t时刻系统工作人员的状态和人数分别用I(t)和N(t)表示,对上述排队系统可构建二维连续时间的马尔可夫链{(I(t),N(t),t≥0)}。状态空间Ω={{(i,n)}∪{(1,j)}∪{(4,0)},i=0,2,3;j=1,2,3,…;n=0,1,2,…},其中 状态转移率图如图1所示,(4,0)对应空闲状态。 图1 状态转移率图 系统稳态存在可由灾难的性质分析得出,故定义稳态概率: 可得出平衡方程,如式(1)—式(9)所示。 (λ+η)π0,0=μqmπ1,1 (1) (λ+η)π0,n=μqmπ1,n+1+μqkπ1,n+λπ0,n-1,n≥1 (2) λπ4,0=μpmπ1,1+ηπ0,0+γπ3,0 (3) (λ+μ+α)π1,1= μpmπ1,2+μpkπ1,1+ηπ0,1+γπ3,1+λπ4,0 (4) (λ+μ+α)π1,n= μpmπ1,n+1+μpkπ1,n+ηπ0,n+γπ3,n+λπ1,n-1,n≥2 (5) (6) (λ+β)π2,n=λπ2,n-1,n≥1 (7) (λ+γ)π3,0=βπ2,0 (8) (λ+γ)π3,n=λπ3,n-1+βπ2,n,n≥1 (9) 由正则化条件式(10): (10) 定义一些母函数: 故式(10)可表示为式(11): G0(1)+G1(1)+G2(1)+G3(1)+π4,0=1 (11) 将式(2)乘以zn,并对n从1到∞求和,再加上式(1)可得式(12): (12) 由式(6)、式(7)可得式(13): (13) 由式(8)、式(9)可得式(14): (14) 对式(5)乘以zn,并对n从2到∞求和,再加上式(2)、式(4)、式(12)和z×式(3),可得式(15): (15) 由f″(z)在0 f′(0)(η+λ)2= [α+μ(1-pk)+λ](η+λ)2-μqη(λ+kη)= (α+μp-μpk+λ)(η+λ)2+μq(η2+λ2+ηλ)-μqkη2= (α+μpm+λ)(η+λ)2+μq(mη2+λ2+ηλ) 因系统稳态存在,在0 γz*G3(z*)-λz*(1-z*)π4,0=0 即如式(16)所示: (16) 结合式(12)、式(13)、式(14)和式(16),代入式(11)可得式(17): (17) 式(17)中: A=λ(1-z*)[γ+λ(1-z*)][β+λ(1-z*)] 由式(17)代入式(16)可得式(18): (18) 由式(17)代入式(13)可得式(19): (19) 由式(17)代入式(14)可得式(20): (20) 式(20)中:y(z)=[γ+λ(1-z)][β+λ(1-z)]。结合式(18)和式(20),代入式(15)可得式(21): (21) 由式(21)代入式(12)可得式(22): (22) 定理2 该队列中,系统中顾客数的PGF(概率生成函数): G(z)=G0(z)+G1(z)+G2(z)+G3(z)+π4,0 该式中各值已由式(18)—式(22)给出。 令系统中的队列长度为L,则系统的平均队长为 工作人员处于休假期的概率: Pv=G0(1)= 工作人员处于忙期的概率: Pw=G1(1)= 工作人员处于延迟期的概率: Pd=G2(1)= 工作人员处于维修期的概率: Pm=G3(1)= 工作人员处于空闲状态的概率: Pi=π4,0= 假设系统原来队长为n,标记顾客到来为队伍中的第n+1个顾客,标记顾客在系统中消耗的时长即为顾客在系统中的逗留时间,用W来表示,W*(s)就是W的拉普拉斯变换(LST)。 定理3 队列中顾客逗留时间的LST: W*(s)= 其中: 证明由强马尔可夫性对5种状态下的标记顾客进行分析。 (23) (24) (25) (26) (27) (28) (29) (30) (31) 对式(23)—式(31)求解,可得式(32)—式(39): (32) (33) (34) (35) (36) (37) (38) (39) 由式(31)—式(34)得式(40): (40) 由式(33)、式(35)和式(40)可得式(41): (41) 由式(32)、式(33)和式(41)可得式(42): (42) 由式(38)、式(39)和式(41)可得式(43): (43) 由式(36)、式(37)和式(43)可得式(44): (44) 队列中顾客逗留时间的LST即为 (45) 将式(31)、式(41)—式(44)代入式(45)。证毕。 本部分通过数值实验解释各参数对系统中平均顾客人数的影响。 令λ=1,η=1.2,β=1.3,r=1.4,q=0.4,p=0.6,k=0.3,m=0.7,得到α和μ对于平均顾客人数E[L]的影响。如图2所示,E[L]随着μ的增长而降低;当保持μ为定值时,α的增长会导致E[L]的降低。由曲线的倾斜程度可知,α的增大会导致μ对E[L]的影响越来越小。这是符合客观实际的,灾难的暴发,会导致所有顾客离开。 图2 α和μ对E[L]的影响 令λ=1,μ=1.6,η=1.2,r=1.4,q=0.4,p=0.6,k=0.3,m=0.7,得到α和β对于平均顾客人数E[L]的影响。如图3所示,E[L]随着β的增长而降低;当保持β为定值时,α的增长会导致E[L]的降低。由曲线的倾斜程度可知,α的增大会导致β对E[L]的影响越来越大。故当灾难爆发的概率较高时,需要提高修理工的到达速度,以加快系统的维修。 图3 α和β对E[L]的影响 令λ=1,η=1.2,β=1.3,r=1.4,α=0.1,q=0.4,p=0.6,得到k和μ对于平均顾客人数E[L]的影响。如图4所示,k趋于0时,服务速率越低,E[L]越大;k趋于1时,服务速率越低,E[L]越小。故当反馈发生频率已知时,需合理选择服务速率,以达到最大的效益。 图4 k和μ对E[L]的影响 本部分对其他带有灾难和伯努利机制的队列中已有的服务效率、灾难发生频率、维修效率进行模拟实验,表明本模型的有效性,在此基础上对反馈部分进行模拟实验,得出相应建议。若社会管理者想要利益最大化,在保证工作台质量和维修效率的基础上还应当根据反馈频率合理选择服务效率。 本文研究了伯努利机制下具有灾难、延迟维修、反馈和休假的单工作台队列,利用马氏链方法和概率母函数技术对系统中顾客人数的稳态概率分布进行分析,给出若干稳态指标,最后利用数值模拟得出建议。在工业、互联网、通讯和高新科技应用中意义重大。本模型还可推广到多服务台、多阶段服务等继续进行研究。

2 稳态分布与系统队长
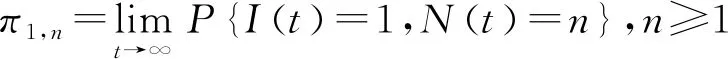
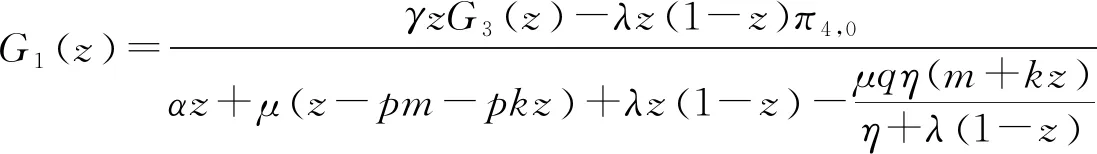

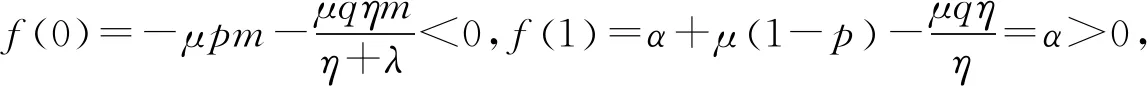
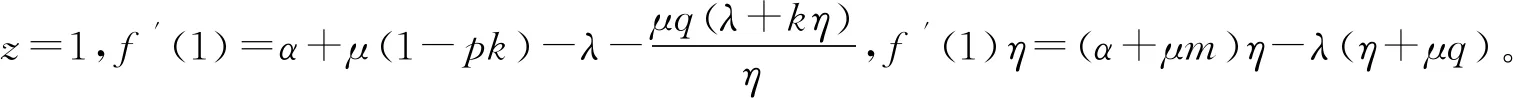
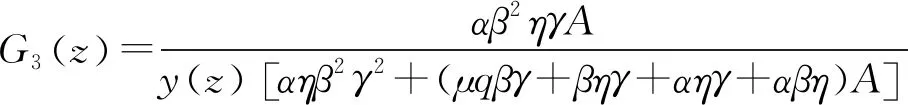
3 性能指标分析
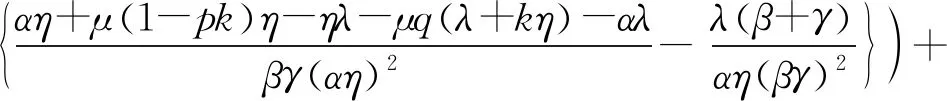
4 稳态逗留时间的LST
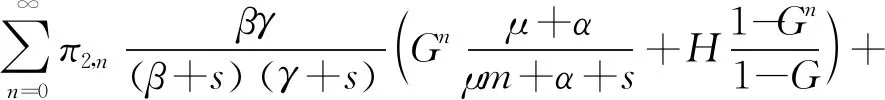
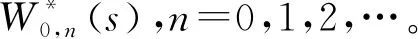
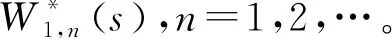
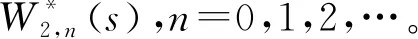
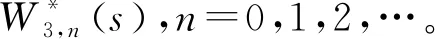
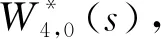
5 数值模拟

6 结 论
