高频数据下基于LSTM的协方差矩阵预测模型

包 悦 妍

(南京审计大学 统计与数据科学学院，南京 211815)

0 引 言

协方差矩阵建模在风险管理、投资组合管理和资产定价方面有着重要的应用。同时，马科维茨[1]投资组合理论的提出进一步推动了协方差矩阵的一系列研究。新时代下大量数据带来了更多新的挑战，比如维数问题导致的估计的一致性、预测的精度等。目前，使用高频日内数据获得更可靠的低频收益率协方差矩阵是较为主流的方法。

Merton[2]最早提出基于日内收益平方和估计波动率的方法——已实现方差(Realized Variance，RV)。随后“已实现”方法也被运用到协方差估计上，得到了已实现协方差；Dong等[3]基于HAR思想和Engle(2002)的动态条件相关系数模型(Dynamic Conditional Correlation，DCC)方法，构造了HAR-DRD波动率矩阵预测模型；Callot等[4]提出VAR-LASSO模型，他们对波动率矩阵做了对数化处理，然后使用向量自回归模型建模，结合LASSO方法对系数矩阵进行降维，估计出具有稀疏特性的系数矩阵；Bollerslev等[5]在已实现协方差矩阵的基础上，将其分解成3部分：正部、负部和混合已实现半协方差矩阵，结果表明半协方差方法对经济信息反应更敏锐，有效提升了投资组合波动率的预测精度。深度学习因为其能处理更多种类的信息被广泛应用于波动率的预测上，如长短记忆神经网络模型(LSTM)、循环神经网络模型(RNN)、卷积神经网络(CNN)等方法。现有的研究一般将深度学习用来预测股票指数的波动率，如Zhou等[6]使用CSI300和百度每日28个搜索关键词作为LSTM模型的输入来预测指数波动率。另外，还有一些学者尝试将深度学习方法和传统时间序列方法结合来预测波动率，如Psaradellis等[7]提出一种将异质自回归模型(HAR)[8]和遗传算法支持向量机模型(GASVR)相结合的方法(HAR-GASVR)对波动率进行预测。许多研究表明深度学习模型在波动率预测与应用方面有着优秀的表现，但仅限于一维情况，对于预测多维协方差矩阵方面的研究几乎没有，深度学习模型的运行过程是个“黑匣子”，模型的解释度差。与深度学习模型相反，时间序列模型虽然对高维数据的处理能力差，但它能够对波动率特有的性质，如长期记忆性、聚集性、杠杆性进行刻画，因此模型的可解释性强。

针对以上问题，提出了基于LSTM模型、DRD分解、半协方差思想和HAR模型的协方差矩阵预测模型(LSTM-SDRD-HAR)。半协方差方法和HAR模型可以反映协方差矩阵存在的长期记忆性和杠杆性，让模型更好理解，LSTM模型则可以提高预测精度，通过模型结合实现预测模型的强解释性和高预测准确度。本文先介绍了关于模型LSTM-SDRD-HAR的构建原理，然后对其进行统计评价和经济效益评价，结果表明协方差矩阵预测模型LSTM-SDRD-HAR的预测精度高，在投资组合中表现优秀。

1 模型与方法

1.1 已实现协方差矩阵与已实现半协方差矩阵

Andersen等[9]于1998年提出了已实现波动率的概念，使得波动率变成“可观测值”，就有了已实现协方差的定义：

其中，RCOVij,t是第i个资产与第j个资产在第t天的已实现协方差，ri,t,k/M为第i个资产第t天的第k个对数收益率，则n个资产的已实现协方差矩阵为

∑t=(RCOVij,t)n×n

Bollerslev等在2020年进一步提出了已实现半协方差的概念。首先，定义函数p(x)≡max {x,0}，n(x)≡min {x,0},然后将已实现协方差矩阵分成3个部分，分别是正部、负部和混合部，假设考虑n个资产，定义分别如下：

1.2 HAR模型

HAR模型可用于描述波动率的长期记忆性，鉴于该模型结构简单且预测效果好，被广泛使用。Chiriac等[10]将HAR模型从一维情形推广到高维情形，得到向量形式的HAR。他们对已实现协方差矩阵∑t进行拉直向量化，由于∑t为对称矩阵，可只将其下三角部分进行向量化Ht=vech(∑t)，则Ht为n*=n(n+1)/2维向量，向量形式HAR模型为

Ht=θ0+θ1Ht-1+θ2Ht-5|t-1+θ3Ht-22|t-1+εt

1.3 LSTM模型

LSTM网络是一种特殊的循环神经网络(RNN)，它与RNN的区别在于中间状态的更新方式不同，这让LSTM能够解决梯度消失和梯度爆炸问题。不仅如此，在处理一些需要长期记忆问题，即当研究的序列较长时，LSTM的表现优于RNN。因此，LSTM模型十分适合用来预测波动率，LSTM模型构建如下：

ft=σ(Wf·[ht-1,xt]+bf)

it=σ(Wi·[ht-1,xt]+bi)

Ot=σ(WO·[ht-1,xt]+bO)

ht=Ot°tanh(Ct)。

1.4 LSTM-SDRD-HAR模型的构建

LSTM-SDRD-HAR模型就是通过整合DRD分解、半协方差、LSTM模型和HAR模型来构建的，具体实施步骤:

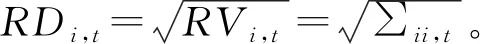
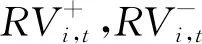
步骤2 对Rt作拉直向量化处理,由于Rt为对称矩阵且主对角线恒为1，只需对其下三角矩阵进行拉直向量化，令yt=vech(Rt)，利用HAR模型对yt进行建模，再返回至矩阵形式。

LSTM-SDRD-HAR模型通过LSTM模型和HAR模型刻画数据的长期记忆性，半协方差方法刻画数据的杠杆性，让模型更容易挖掘数据的特征，并且针对波动规律不同的部分Dt和Rt分别建模，具体问题具体分析，有利于找寻各自规律，提高模型的预测精度。

2 实证分析

实证采用上证50成分股中10只股票的5 min交易数据，这10只股票的选取方法是将成分股的股票代码从小到大排序，取排在前10的股票。5 min高频收益率数据来源于锐思数据库，时间跨度为2004-01-02—2019-12-31，将整个数据样本分为样本内数据和样本外数据，样本内数据为2004-01-02—2016-02-05期间数据，共2 850个交易日，样本外数据为2016-02-06—2019-12-31期间数据，共943个交易日。

2.1 数据处理

根据10只股票的5 min高频收益率计算已实现协方差矩阵。计算已实现协方差矩阵时，若某只股票缺失数据很多，将会出现已实现协方差矩阵不正定的情况，会给估计和预测带来较大误差，所以对交易日进行剔除处理，删去数据缺失率达到25%的交易日，剔除后剩余3 793个交易日。对于数据缺失量少于25%的交易日内数据，进行缺失值填补，填补规则为采用上一个时间段的收盘价价格，作为该时间段的收盘价格，计算出该5 min收益率。

表1展示了分解后10只股票已实现波动率Dt的均值与标准差，还有相关系数矩阵Rt的平均水平。从表1可知：10只股票的已实现波动率均值在0.02附近，且不同股票的已实现波动率相对差异较大，体现了已实现波动率的相对独立特性。此外，这10只股票对应的已实现波动率标准差相近，一定程度上反应了10只股票的流动性和上证50市场的特性，即当市场报价集中在一个共同价格水平附近，市场的买方和卖方都愿意在当前价格附近，以较小的价差执行股票交易，波动率会较低且保持稳定。流动性强的市场会有更多的机遇，投资者通过合理制定投资策略就可以实现获利。在研究相关关系时，相关系数大于等于0.3，就可以认为数据存在相关关系，从表1相关系数矩阵Rt的均值可以看出，同一市场内一些股票之间的相关性很小，但其他股票之间有相关关系，研究清楚其中的关系，有利于对已实现协方差矩阵更准确地预测并做出投资计划。在此，研究上证50的这10只股票是有意义和价值的。

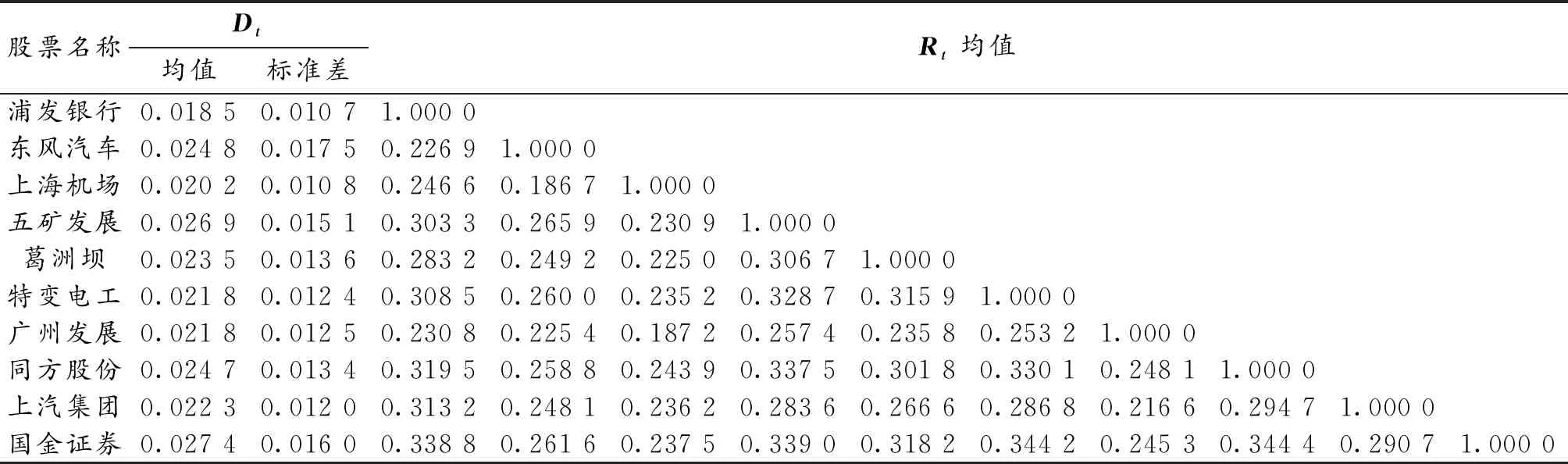
表1 描述性统计

经过比较每一只股票的已实现波动率RDi,t和已实现相关系数Rt(i,j)时间序列图，发现已实现波动率RDi,t和已实现相关系数Rt(i,j)的变化规律不同，限于篇幅，下文仅以浦发银行为例。图1描绘的是第一只股票浦发银行的已实现波动率RD1,t，大致在2008年和2016年，RD1,t波动得比较剧烈，整体上波动幅度不大，较为稳定；图2描绘的是浦发银行与第二只股票东风汽车的已实现相关系数Rt(1,2)，其波动幅度大，说明已实现相关系数Rt(1,2)反映了一定时间内市场情况的变化。比较图1和图2，可以直观地看到：已实现波动率Dt和相关系数Rt两者的形态是不同的，已实现波动率Dt的时间序列图有明显的波峰，变化值小且稳定；而相关系数Rt波峰不明显，波动大且频繁，因此有必要对Dt和Rt分别进行研究。

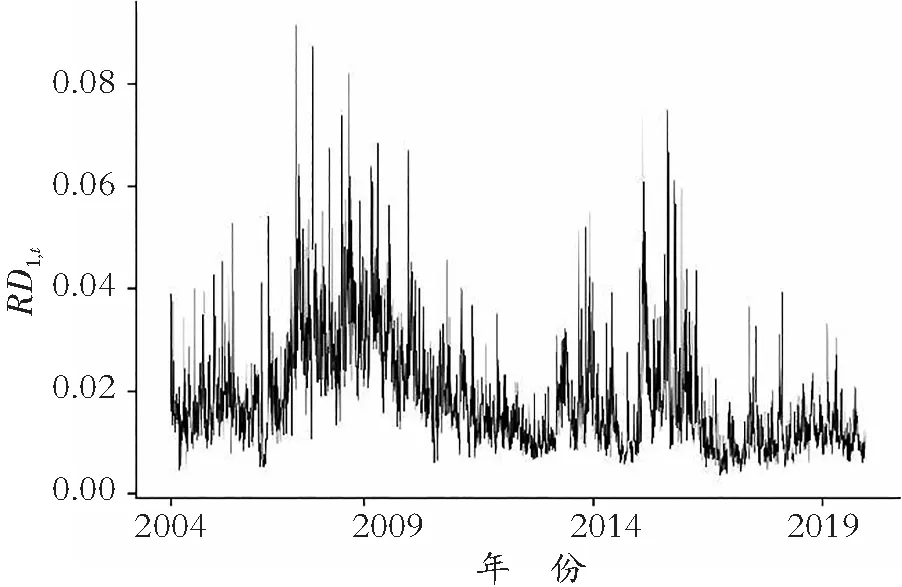
图1 已实现波动率RD1,t时间序列图

图2 相关系数Rt(1,2)时间序列图

2.2 预测评价

选取均方根误差，FRMSE和均方误差FMAE这两个指标来评价已实现协方差矩阵预测模型的预测能力，指标定义如下：

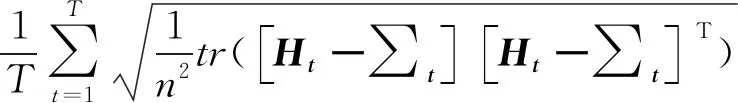
在实证研究中,n=10，T=943。

为了展示构建的已实现协方差矩阵的预测效果，在此将其与HAR、EWMAQ、HAR-DRD、LASSO-VAR、LASSO-DRD、LSTM-DRD-HAR模型进行比较。

表2展示了7个模型在样本外的预测误差，可以看到HAR模型存在的明显问题就是预测效果差。EWMAQ模型是在指数移动平均模型(EWMA)的基础上将估计误差考虑进模型的调参过程，结果显示这个做法确实带来了预测效果的提升，结果与HAR-DRD模型相差无几，但EWMAQ在计算过程中会涉及四阶矩，计算较为复杂且耗时久。与EWMAQ相比，剩下6个模型的计算过程简便且耗时短。表2结论主要如下：对比HAR和HAR-DRD、LASSO-VAR和LASSO-DRD模型发现，经过DRD分解再建模比不分解直接建模预测结果更准确，这说明事先进行DRD分解是有必要的，它将不同结构的组成部分分离开来，对不同部分建模找寻各自的规律可以提高准确性，所以考虑的模型中大部分都采用了DRD分解；表中预测效果最好的是LSTM类模型，LSTM算法比LASSO算法的模型精度提升至少8%，LSTM-SDRD-HAR的样本外预测结果仅次于LSTM-DRD-HAR。总体来说，DRD分解和LSTM模型能有效改进模型预测精度，并且不会增加计算复杂度。

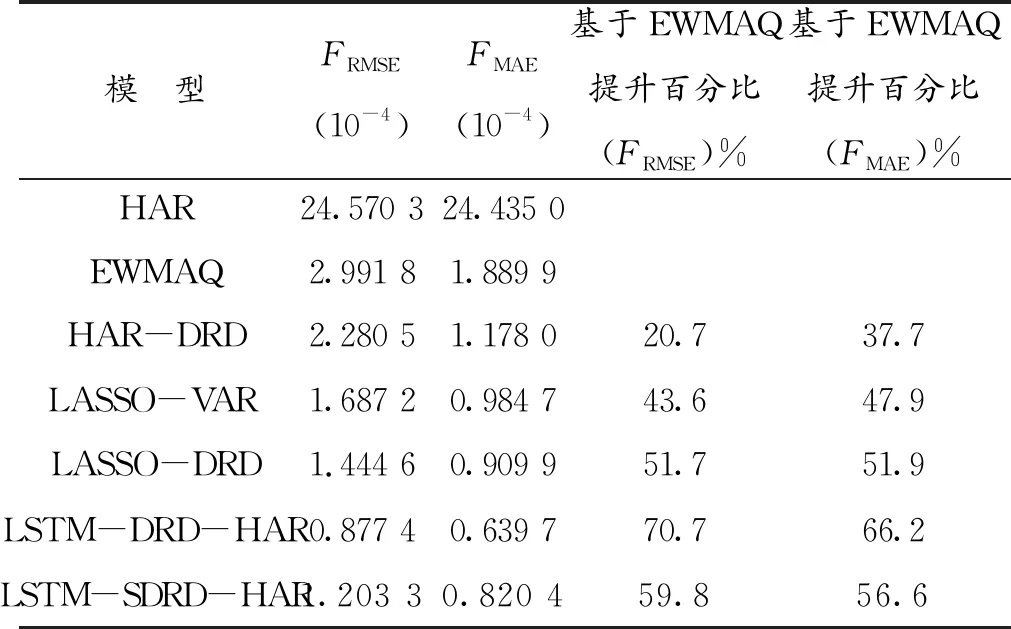
表2 已实现协方差矩阵样本外预测结果

2.3 经济评估

为了评估波动率矩阵预测的经济价值，考虑马科维茨有效前沿。假定投资者是风险厌恶型的，则在相同的年化预期收益率μp下，他们会选择风险更小的资产；同样地，如果风险水平相同，投资者们就会选择高收益资产。在这里，最优投资组合就是下面这个问题的解：

图3中“Oracle”代表的是理想情况，在所有有效前沿的上方，很明显它是最优的。星标的位置表示全局最小方差组合，从图3可以看出：HAR模型的全局最小方差组合风险最大，收益仅高于EWMAQ模型；而EWMAQ模型的全局最小方差组合的收益最低。在经济评价中也有着和统计评价相一致的结果：LSTM类模型的全局最小方差组合风险最小，因为模型LSTM-DRD-HAR精准的预测，所以其有效前沿曲线与理想情况相近，而模型LSTM-SDRD-HAR因为对重大事件敏感，所以能有效规避风险，在同等的风险水平下获得更高的收益；LSTM类优于LASSO类模型，LASSO类又优于HAR、EWMAQ和HAR-DRD类；考虑DRD分解的模型，它们的有效前沿曲线在没有考虑DRD分解模型的上方，说明DRD分解也有利于改善经济评价。综上，LSTM算法和DRD分解不仅可以提高预测精度，在投资组合优化方面也起到了积极作用，其中模型LSTM-SDRD-HAR的综合评价最高。

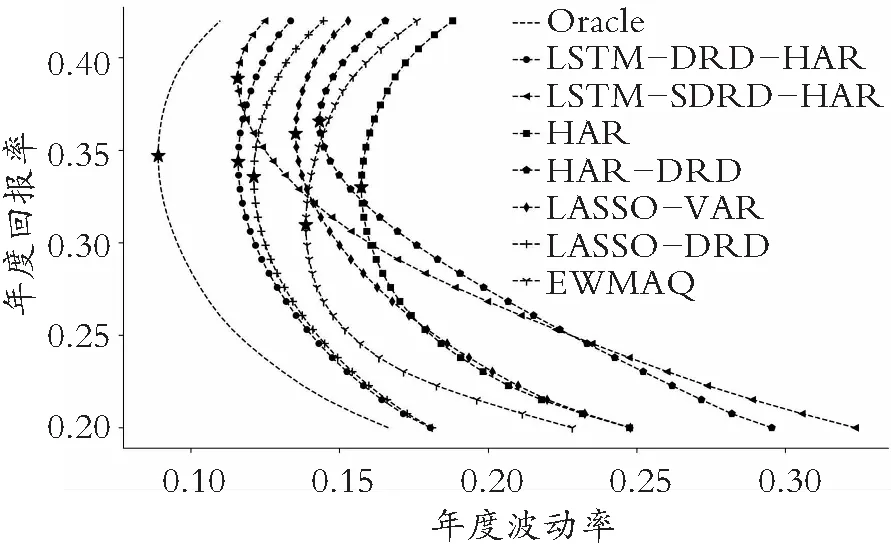
图3 马科维茨有效前沿图

3 结 论

近年来，深度学习在预测低维时间序列时表现出很好的预测效果，如何利用深度学习预测优势，结合传统时间序列模型的特征优势，从而提升协方差矩阵的预测能力，值得深入分析与研究。