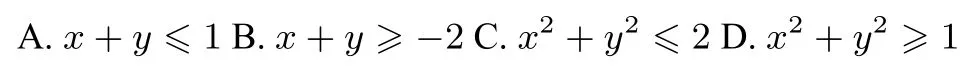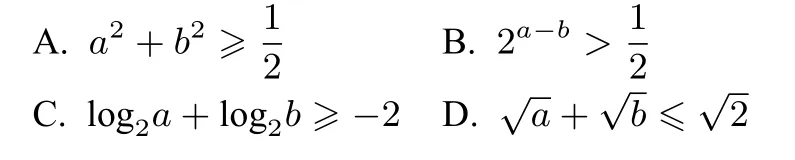一道清华大学新领军TACA 试题背景揭示与多解
2023-01-02山东省宁阳县复圣中学271400张志刚
山东省宁阳县复圣中学(271400) 张志刚
二元方程约束条件下的最值问题解法灵动多变,饱含数学思想,备受命题专家的青睐,成为历年高考考查的热点,近三年就有2020 年新高考全国I 卷第11 题、新高考全国II 卷第12 题、天津卷第14 题、江苏卷第12 题,2022 年新高考全国II 卷第12 题等进行了独立考查.近年,此类问题也逐渐进入竞赛、高校强基计划测试等选拔性考试,增添了一道靓丽的风景线.与高考试题相比,题目涉及知识点更多,思维跨度更大,呈现出更强的综合性与选拔性.
1 试题呈现
题目(2022 年清华大学新领军TACA 数学二试题第2题)已知正实数a,b满足a+2b=1,I为的最小值,则[I]=____.
注: 若实数a满足n≤a 本题设计简洁凝练,构思别具匠心,考查方程条件下的二元函数最值问题,突出考查数学抽象、逻辑推理、数学运算等核心素养. 本题命制的背景是应用拉格朗日乘数法求极值问题.其原理是: 给定二元函数z=f(x,y) 和附加条件φ(x,y)=0,为了探求z=f(x,y) 在附加条件下的极值点,先构造拉格朗日函数L(x,y)=f(x,y)+λφ(x,y)(λ为参数),计算L(x,y)对x,y的一阶偏导数,令它们分别为零,并与附加条件联立,即 图1 应用拉格朗日乘数法本题解答如下: 由于a >0,b >0,且a+2b=1,令 拉格朗日乘数法在理论上是经济便捷的,但在实际解题过程中,中学生却面临不小的挑战: 首先,学生理解拉格朗日乘数法的原理需要较长的过程;其次,求偏导运算对于高中学生而言也是陌生的;此外,求解方程组需要较强的运算求解能力,等等.那么,如何用初等数学方法解决呢? 在高中阶段,解决此类问题可从方程有解、不等式放缩、函数最值等视角尝试解答.减元思想是贯穿解题过程的一条主线,即把双变量问题转化为一元函数或方程问题,再辅以换元法、构造法、放缩法、配方法及函数与方程、转化与化归、数形结合、分类讨论等数学思想方法,实现消元、降幂、化简之目的. 思路一 转化为二次方程有解问题 判别式的符号与二次方程解的个数息息相关,利用判别式成为处理二次方程问题的常规操作.本题中令=z,借助条件a+2b=1 消元得(1+2z)b2−(z+2)b+3=0.当1+20 时,利用二次方程有解判别式∆≥0 建立关于z的不等式. 解法1 判别式法 评注“二次方程有解则判别式大于等于0”是学生最早接触、最为熟悉、最易掌握的方法.美中不足的是,上述解答在得到方程(1+2z)b2−(z+2)b+3=0 后,需对二次项系数分类讨论,如何规避分类讨论简化问题呢? 由于“三个二次”紧密相联,可转而讨论相应不等式成立的情况. 思路二 转化为不等式恒成立问题 解法2 (解法1 优化)判别式法 思路三 运用不等式放缩求解最值 解法3 基本不等式法 因为a>0,b>0,由基本不等式得 评注以上通过典型的“1”的代换,将目标函数的分子化为关于a,b的二次齐次式,进而借助基本不等式求得最值.此外,利用基本不等式要注意验证等号能否成立. 思路四 通过消元转化为一元函数最值 通过哪些渠道将本题的二元函数转化为学生熟悉的一元函数呢? 由题设得a=1−2b,代入目标函数有,即转化为关于b的一元函数,此时可考虑导数方法(解法4)、齐次化消元(解法5)等讨论最值;由a+2b=1 联想到等差中项,通过构造等差数列也可实现减元(解法6). 解法4 导数法 导数是关于瞬时变化率的数学表达,定量刻画了函数的局部变化规律,利用导数可以精确地研究函数的单调性、最值、增长(衰减)率、增长(减少)快慢等性质. 评注通过以上过程,我们可进一步体会导数讨论函数(含高次多项式函数、分式函数、三角函数、数列等)单调性的普适性,体会知识之间的有机衔接与融合. 解法5 齐次化消元 解法6 构造等差数列减元 思路五 利用实数域内平方式的非负性 配方是一种以“出现平方式”为思维指向的恒等变形,因而,配方法既具有一般恒等变形的功能,又具有“平方式”,从而在实数范围内产生非负数的特殊功能.至于配方法的更多作用,如配方消去一次项、配方分离分母等,都可以分解成这两个基本功能的组合与派生[1]. 解法7 配方法 体现出配方变形的靶向性、不唯一性、灵活性. 追根溯源可以直击命题意图,横跨纵联也利于培养学生的发散思维等创新性思维.以拉格朗日乘数法为背景的二元方程条件下的最值问题意蕴丰富,包含函数、方程、不等式、三角代换等高中数学主干知识.对于此类问题,教师要充分挖掘其意境高深悠远、再生能力强、探究空间大的优势,引导学生捕捉信息,挖掘本质,抓住关键,寻求联系,构建方案.学生在感知确认、抽象概括、合情推理、操作运算等思维活动中,全方位、多角度、多层次地思考问题,综合运用各种方法,提出新视角、新观点、新设想,逐步学会有逻辑地思考数学问题. 最后再给出几题,供读者练习. (1)(2022 年新高考全国Ⅱ卷第12 题)对任意x,y,满足x2+y2−xy=1,则() (2)(2020 年新高考全国I 卷第11 题)已知实数a >0,b>0,且a+b=1,则() (3) (2017 年清华大学领军计划测试第6 题) 已知x2+xy+y2=1,则()2 命制背景

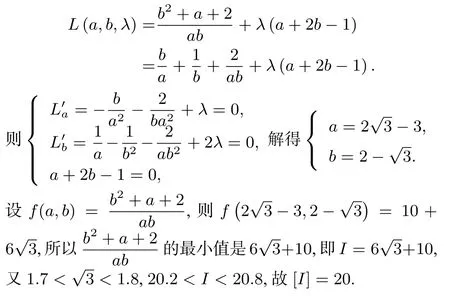
3 试题解答








4 结束语