高中数学中的常见不等式及其应用

广东省中山纪念中学(528454) 邓启龙

均值不等式,柯西不等式等一系列不等式,是证明不等式的重要依据和方法,是研究最值问题的强有力的工具,这些高中数学中的常见不等式在解题中具有广泛的应用.

首先给出高中数学中的常见不等式.

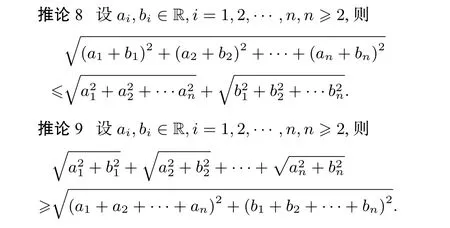
以上这些常见不等式和推论在证明不等式和求最值中具有广泛的应用.

一、运用常见不等式证明不等式

二、构造函数证明不等式

三、换元后证明不等式和求最值

注证法一通过整体换元后利用伯努利不等式来证明结论,思路非常巧妙.证法二根据题目的结构特点进行配凑,然后利用杨氏不等式证明结论,直接有效.

3.已知a,b,c≥ 0,证明:a(a −c)2+b(b −c)2≥(a −c)(b −c)(a+b −c).

证明令x=a −c,y=b −c,则c≥0,c≥−x,c≥−y,且a=c+x,b=c+y.于是

注若题目中出现两个变量的差,可考虑将差值换元,简化表达式.

四、配凑和拆分

注根据题目的结构特点引入参数,将1 拆成λ+1−λ,然后利用柯西不等式,并由系数的比例关系求出参数,进而解决问题.

5.已知∆ABC的三边分别为a,b,c,2a+7b+11c=120,求∆ABC的面积的最大值?

解由海伦公式得∆ABC的面积

五、反证法

六、配对