探究圆锥曲线关于切线长的统一恒等式

广东省中山市桂山中学(528463) 谭天众

1 背景

文[1]给出以下结论:

性质1已知O为坐标原点,点T(x0,y0)为圆锥曲线C上一点,C在点T处的切线为l,点P是l上的任意一点(和点T不重合),过点P作OT的平行线交圆锥曲线于不同的两点A,B,则λ=为定值.

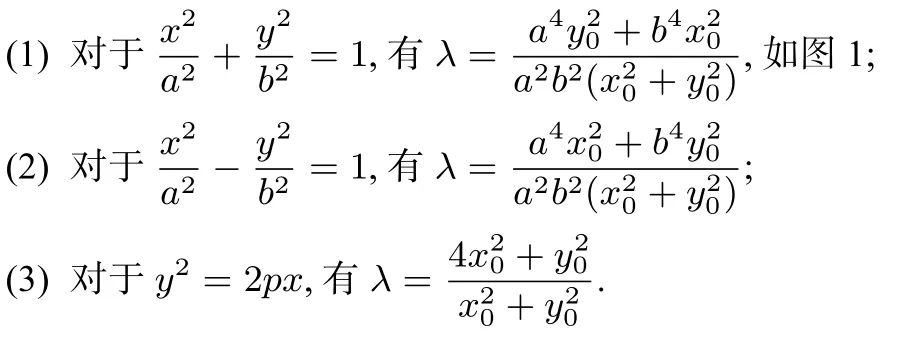
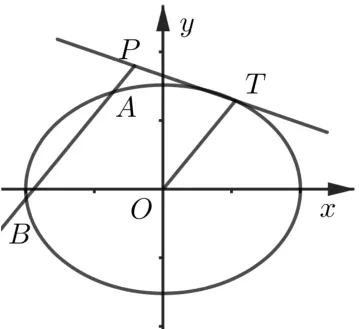
图1

文[2]给出以下结论:

性质2 (1)如图2,已知点P在椭圆C:=1上,点Q(m,n)不在椭圆C上,过点Q作平行于OP的直线

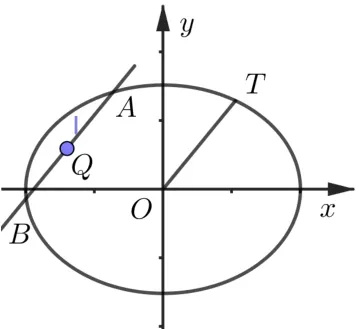
图2

我们发现两个结论之间有联系,并思考能否将两个结论结合起来得到更优美的结论呢?

2 探究与结论

证明已知O为坐标原点,点T(x0,y0)为椭圆C上一点,C在点T处的切线为l,点P(xp,yp)是l上的任意一点(和点T不重合),过点P作OT的平行线交椭圆于不同的两点A,B,则由性质1(1)得到,

与椭圆的情形类似,我们可以得到双曲线的如下等式,因其证明与椭圆的情形相似,不再赘述.

再研究抛物线y2=2px的情形.

引理2 已知T(x0,y0)是抛物线C:y2=2px上的非顶点的点,点P(xp,yp)不在抛物线C上,过点P作平行于OT的直线抛物线C于A,B两点,则

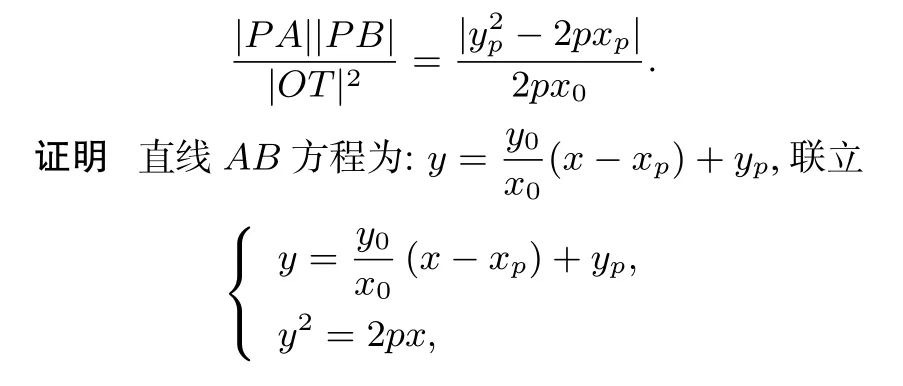
恒等式3 过点P(xp,yp)作抛物线y2=2px的两条切线,T,Q的两分别为切点,F为抛物线的焦点,则

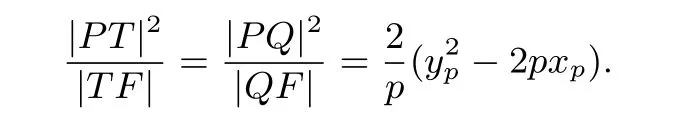
证明设O为坐标原点,点T(x0,y0)(非原点)为抛物线C上一点,C在点T处的切线为l,点P(xP,yP)是l上的任意一点(和点T不重合),过点P作OT的平行线交抛物线于不同的两点A,B,由性质1(3)得到

以上三个恒等式如果用语言表述,可以表述为“过圆锥曲线外一点作圆锥曲线的两条切线,则切线长平方与切点的焦半径的乘积之比相等”,统一简洁优美.