基于Simulink车辆独立悬挂空间运动特性建模分析

2022-12-30陈小龙韦超毅梁雪梅

机械设计与制造 2022年12期

陈小龙，韦超毅，梁雪梅

（1.广西工业职业技术学院车辆工程学院，广西南宁 530001；2.广西大学机械工程学院，广西南宁 530004）

1 引言

悬挂系统一端承载车架，另一端与车轮相连，传递二者之间的力和力矩，同时通过阻尼和刚度变化衰减来自路面激励的冲击和振动，使得整车可以平稳运行。同时，悬挂系统有效保证车辆在不同的激励和承载条件，整车运行的平稳性，使得整车保持良好的操纵稳定性[1]。当车辆从满载变化到空载时，因簧上载荷的变化，悬挂的弹性伸缩，车轮的定位参数将发生变动，而当车轮上下跳动或车身侧倾时也亦将如此。而在车轮定位参数变动时，因转向系统与悬挂导向机构的运动耦合，前轮将产生附加转向效应，即前轮摆动误差。悬挂系统的运动变化将引起车辆转向性能的优劣，因此对悬挂系统进行运动学特性分析，对车辆转向系统研究具有重要意义。

国内外学者开展了一定的研究：文献[2]采用多体动力学模型，对转向工况下，车辆悬挂主销倾角随转向角变化规律进行分析；文献[3]采用振动台架，对周期性激励下，悬挂系统的垂向加速度变化规律进行分析；文献[4]分析不同的承载工况下，车轮的轮跳对侧向加速度的影响规律，以此作为设计的依据；文献[5]搭建四分之一车辆模型，对轮胎参数变化对悬挂系统的振动特性进行分析，以此设计连接减振结构。学者们的研究对空间运动特性分析较少，承载变化的影响较少涉及，这都是影响转向系统的重要因素，针对此开展研究。

根据纵横复合连杆式独立悬挂的空间结构特点，对其进行简化；依据多刚体系统运动学的相关理论，在考虑悬挂缸的动刚度特性的前提下，对车轮定位参数变化、车轮跳动时摆动误差及滑移量等进行分析，建立悬挂系统的空间运动数学模型；基于Simulink 建立悬挂系统空间运动分析模型，获取空载和满载工况下，车辆发生转向，轮胎跳动时，车轮跳动的摆动误差及滑移量变化规律。

基于实车测试，获取整车满载工况，30km∕h运行时，实车和仿真模型的悬挂系统竖直方向跳动加速度和功率谱，以此验证数学模型、仿真模型和分析结果的准确性。

2 悬挂系统空间运动特性分析

所研究的纵横复合连杆式独立悬挂的空间结构图，如图1所示。右侧轮悬挂机构简图，如图2所示。该悬挂主要包括横向连杆、纵向斜连杆、油气悬挂缸筒及其活塞杆，其横连杆、斜连杆通过关节轴承直接连接车架和油气悬挂活塞杆，而油气悬挂缸筒也通过关节轴承直接与车架相连，一起承受行驶过程中轮胎传递来的力和力矩[6]。油气悬挂缸筒和活塞杆之间充高压油液和气体，共同起到弹簧、阻尼的作用。

图1 独立悬挂三维实体Fig.1 Independent Hanging 3D Solid

图2中，E、F、G、H和I处都为球副，O1为圆柱副，O1F之间为滑移副，同时E、H、G、I点为横向连杆、纵向斜连杆的各球副中心，F点为油气悬挂缸筒的球副中心。在悬挂数学建模时，假设车辆在满载工况下为其模型的初始状态，同时全部铰接点为无间隙配合，且各杆件均为刚体[7]。

图2 右侧轮悬挂机构简图Fig.2 Schematic Diagram of Right Wheel Linkage

设各个铰接点在基础坐标系O-xyz的初始坐标：E（xF，yF+Y，Z1−Z），F（xF，yF，Z1），O1（0，yO1，0），H（xH，yH，zH），I（xI，yI，zI），G（xF+X，yG，zI）。根据车架及车身高度的设计要求，初始时，设定Y表示为E、F两点间横向距离，Z表示为E、F两点间垂向距离，Z1表示为O1、F两点间垂向距离，X表示为E、G两点间纵向距离，L1H表示为O1H的长度，L1I表示为O1I的长度。同时，根据机构的连接，则有关系式：

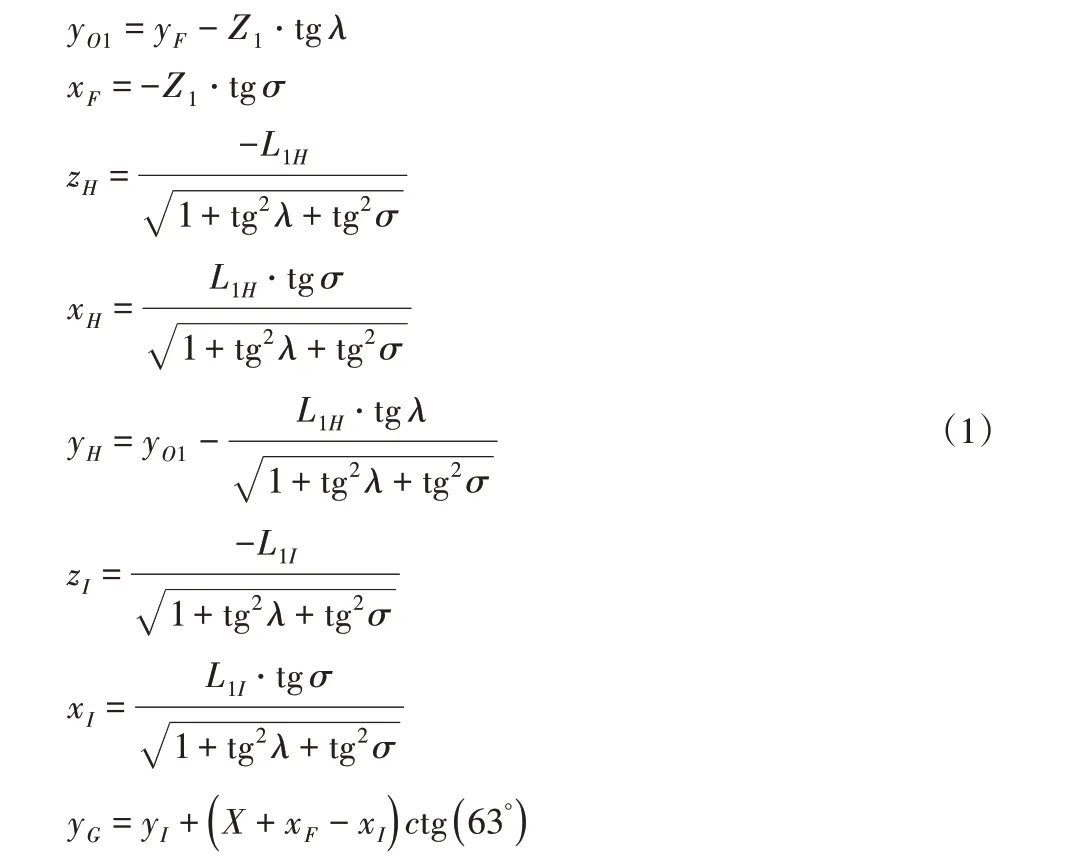
其中，63°角为设计纵向斜拉杆时的限制要求。

当簧上质量从满载到空载变化时，假设车身相对大地不动，基础坐标系O-xyz保持不动，则由于悬挂缸的伸长，使得悬挂缸的一端与横向连杆、纵向斜连杆铰接连接的点H、I，在向下运动的同时，绕着E、G点旋转，从而主销倾角发生变动；由于横拉杆AB，CD的长度一定，簧上载荷变化过程中，转向节臂O1A，O3D杆绕主销转动，带动两侧车轮绕主销转动，引起转向轮的偏转，使得车轮外倾角、前束值也随前轮载荷的不同而变化[8]。

2.1 主销倾角变化

设定簧上质量从满载变化到空载时，悬挂缸的伸长量为L，设此时点O1k、Hk、Ik的坐标变为：O1k（xO1k，yO1k，zO1k），Hk（xHk，yHk，zHk），Ik（xIk，yIk，zIk），主销内倾角变为λk，主销后倾角变为σk，有关系式：

联合求解，可得内倾角λk、主销后倾角σk及点O1k、Hk、Ik坐标，由此即可得到车辆从满载到空载变化时，内倾角及主销后倾角的变化。

2.2 前束值变化

对于转向机构球头A，设其在悬挂缸伸长L时，前束角变为δk，坐标变为Ak（xAk，yAk，zAk）。由于点O1上的辅助坐标系O1−x1’y1’z1’在主销倾角变动时，随着主销倾角的变化的旋转[9]，因此球头A，在变化前后，其相对于点O1上的辅助坐标系O1−x1’y1’z1’的坐标一直保持不变，即则有：

2.3 外倾角变化

同理，对于车轮外倾角的变化，当前束角变为δk时，设车轮的法向矢量变为SMδk（SMδkx，SMδky，SMδkz），则有：

联合求解，可得外倾角ηk，由此即可得到车辆从满载到空载变化时，车轮外倾角的变化。

3 基于Simulink运动特性分析

根据数学模型分析，基于Simulink建立悬挂系统空间运动分析模型，如图3所示。

图3 悬挂系统运动分析模型Fig.3 Motion Analysis Model of Suspension System

分别获取空载和满载工况下，车辆发生转向，轮胎发生跳动时，车轮跳动的摆动误差及滑移量变化曲线，如图4所示。

图4 满载轮跳时变化曲面Fig.4 Change Surface of Full Load Wheel Jump

整车的设计参数需要满足，跳动控制在90mm范围内，摆角误差控制在1°内，滑移量不得超过20mm。由图中结果可知，满载工况下，车轮跳动达到90mm、内侧轮胎转角达到40°时，摆动误差为0.39°，车轮跳动达到−90mm、内侧轮胎转角达到6°时，滑移量达最大为11.3°；空载工况下，车轮跳动达到90mm、内侧轮胎转角达到−30°时，摆动误差为0.16°，车轮跳动达到−90mm、内侧轮胎转角达到3°时，滑移量达最大为16.3°，均满足设计要求。