基于小波变换的双阈值水下焊缝图像边缘检测研究

李盛前，张小帆

(1.广东机电职业技术学院电气技术学院，广东广州 510550；2.广东技术师范大学汽车与交通工程学院，广东广州 510665)

0 前言

图像处理是水下焊接机器人视觉伺服自动跟踪焊缝系统的关键技术之一，视觉伺服水下焊接机器人利用视觉传感器感知外界事物，通过视觉传感器获取外界图像并进行图像加工处理，识别出物体特征，即实现对外界事物的理解，其中图像的边缘作为物体在图像中特征信息的反映,它是识别物体的重要依据,是图像的最基本特征[1]。通过对图像边缘的检测提取可以对目标进行识别、图像分析等，所以图像边缘检测是图像处理和计算机视觉技术的一个热点研究课题。

目前，随着相关科研人员的不断探索，形成了一些典型的图像边缘检测算法[2]，如Roberts算法、Sobel算法、Prewitt算法、Laplace算法、Kirsch算法、LOG算法。这些算法普遍利用平滑函数处理后的图像寻找一阶导数局部极大值点来检测边缘，但是它们对噪声非常敏感，以致边缘检测结果不是很理想。1986年CANNY[3]应用最优算子，较好地确定了图像灰度突变位置，这就是被人们公认的对图像边缘检测效果较好的Canny算法。虽然该算法完全可以胜任噪声污染不是很严重的图像边缘检测，但对水下焊接环境中获取焊缝图像后进行边缘检测显得无能为力，主要原因为Canny算法都是在同一个尺度中检测的，无法进行多尺度抑制污染噪声，对图像边缘由粗到细检测。1992年，MALLAT首次使用二次B样条小波对图像边缘进行检测，检测结果较好，这为小波边缘检测奠定了基础[4]，后来专家们根据此法，主要对小波函数构造、阈值设置、多尺度分解改进，提出了各种算法[5-9]。

综述现有文献，本文作者基于Canny算法思想，结合小波变换，对Canny算法非极大值抑制、高低阈值设置进行改进，提出基于小波变换的自适应双阈值边缘检测算法，并应用该方法对水下焊缝图像边缘进行检测，解决抑制噪声和边缘由粗到细检测的矛盾，提高水下焊缝边缘检测的精度和完整性。

1 问题描述

图像处理是水下焊接机器人视觉伺服跟踪焊缝控制系统的重要环节，系统组成如图1所示。可以看出，要实现机器人对焊缝自动跟踪，必须给焊接机器人实时提供水下焊缝的位姿信息，将CCD采集的焊缝图像进行去噪处理，根据摄像机成像原理计算得到焊缝空间三维位姿信息。其中，焊缝图像边缘检测是最底层，也是最重要的任务，焊缝边缘检测的质量决定了焊接机器人自动跟踪系统工作的性能及焊接跟踪精度。

图1 水下焊接机器人视觉伺服跟踪系统组成框图

2 基于多尺度小波变换的改进Canny算法

近几年，小波变换在图像处理领域中应用非常活跃，由于小波变换[10-11]通过压缩和平移等处理功能，能够对图像或信号进行多尺度详细分析检测，小波变换成为图像处理的一种新兴技术手段[12-14]。由于水下的环境特殊，CCD获取的焊缝图像受到的噪声影响非常大，经过试验验证，Canny算法无法胜任对水下焊缝图像边缘的检测。因此，本文作者提出一种利用多尺度小波变换和Canny算法相结合对图像边缘检测的算法，解决上述问题，并对受高噪声影响的水下焊缝进行焊缝边缘检测，验证所提算法的实效性和可行性，确保对水下焊缝图像边缘检测提取的准确性和完整性。

2.1 小波变换定义

小波定义：设φ∈L2(R)∩L1(R)，且满足条件：

(1)

对二维连续小波函数进行二进变换离散化得到二进小波函数：

(2)

设二元平滑函数θ(x,y)，设：

(3)

(4)

所以转换为二进小波函数得：

(5)

(6)

又因为：

(7)

(8)

f(x,y)⊗θ(x,y)≈f(x,y)

(9)

所以图像的边缘点反映到函数f(x,y)就是函数值的突变点，于是对f(x,y)⊗θ(x,y)求导可以确定这些边缘点。

(10)

(11)

其中：j为多尺度的分解层次，通过取不同的j，可实现多分辨率小波变换边缘检测，即多尺度小波变换边缘检测。同时由上式可看出，如果平滑函数取高斯滤波函数时，算法就变成了传统Canny算法。

由式(10)(11)，可以得到f(x,y)⊗θ(x,y)的梯度矢量表示为

(12)

可得其模值和相角分别为

fM2j(x,y)=

(13)

fA2j(x,y)=

(14)

可知：若fM2j(x,y)沿着相角方向fA2j(x,y)上为局部极大值时，点(x,y)为候选边缘点，边缘的走向与fA2j(x,y)方向垂直。

2.2 小波函数选取

为更好地去除噪声增强图像，尺度函数和小波函数的选取非常重要。在小波变换边缘检测算法中，根据文献[15-16]，小波函数选取B样条且其紧支集性质优于高斯函数，利用B样条作为平滑函数的多尺度边缘提取对大多数应用问题是渐进最优的。同时，它对应的离散小波变换中，快速分解和重构计算量少，过程简洁，因此本文作者选取三次B样条函数作为尺度函数。小波的滤波器系数如表1所示。

表1 小波的滤波器系数

2.3 非极大值抑制

传统Canny算法中的非极大值抑制只对该点梯度方向上的两个邻域梯度幅值进行比较，判断该点是否为局部极大值点，这样的判断结果并不是很精确。改进的非极大值抑制方法中采用双线性插值的方法对当前点与插值结果的点进行比较，以判断当前点是否为局部极大值。插值方法如图2、图3所示，将当前点的4个象限分成八领域。

(1)当0≤θ<90°时，主要在第一、三象限中进行双线性插值。插值方法如图2所示。

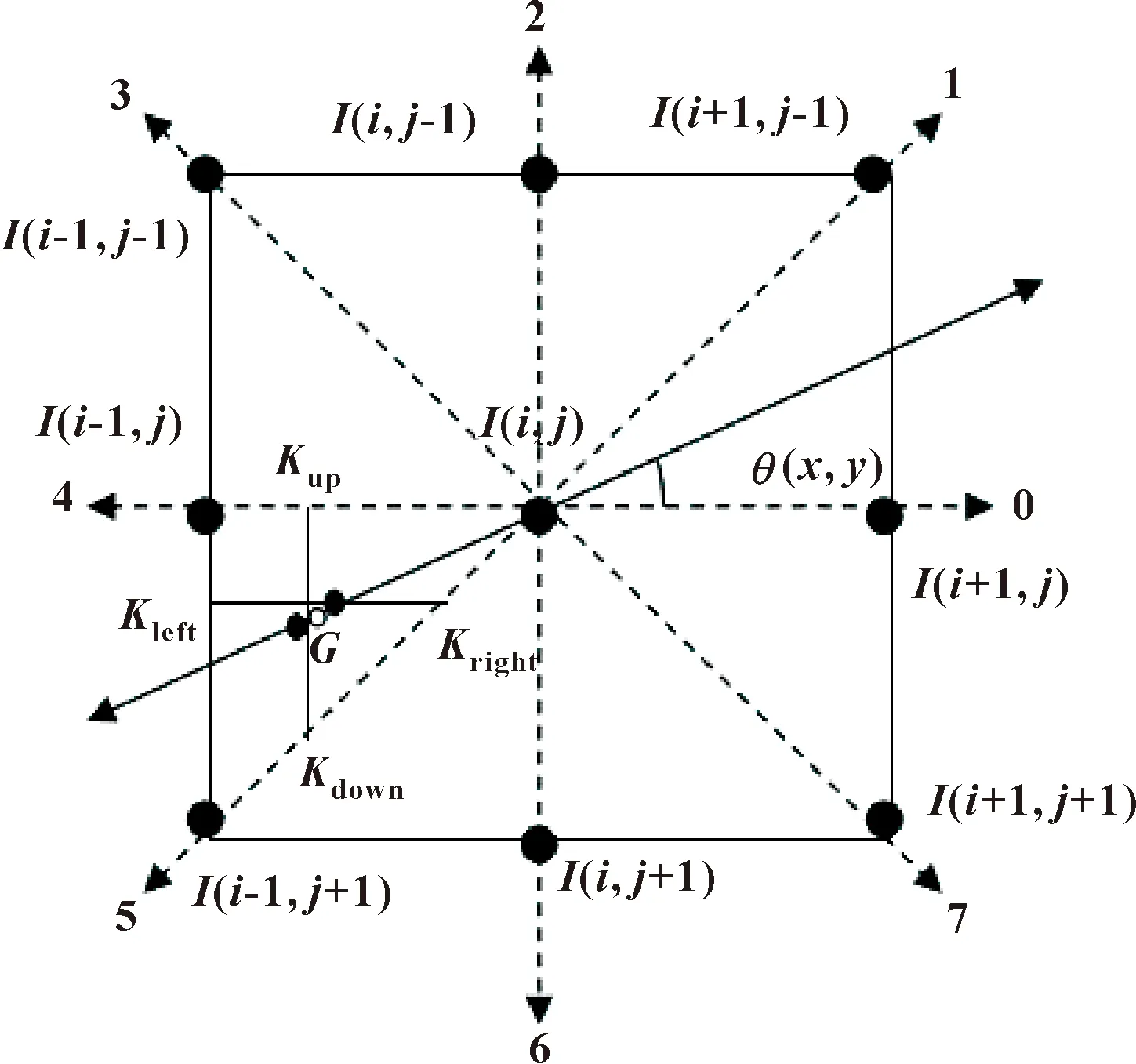
图2 0≤θ<90°插值方法示意

在第一象限中，梯度幅值线性插值过程：

Kup=α[G(i-1,j)+G(i-1,j-1)]+

cos[θ(i,j)][G(i-1,j-1)-G(i-1,j)]

(15)

Kdown=α[G(i,j)+G(i,j+1)]+

cos[θ(i,j)][G(i,j+1)-G(i,j)]

(16)

Kleft=α[G(i,j)+G(i-1,j)]+

sin[θ(i,j)][G(i-1,j)-G(i,j)]

(17)

Kright=α[G(i,j+1)+G(i-1,j+1)]+

sin[θ(i,j)][G(i-1,j+1)-G(i,j+1)]

(18)

Gx=Kdown+sin[θ(i,j)][Kup-Kdown]

(19)

Gy=Kleft+cos[θ(i,j)][Kright-Kleft]

(20)

(21)

同理，第三象限梯度幅值线性插值过程为

cos[θ(i,j)][G(i+1,j-1)-G(i+1,j)]

(22)

cos[θ(i,j)][G(i,j-1)-G(i,j)]

(23)

sin[θ(i,j)][G(i+1,j-1)-G(i,j-1)]

(24)

sin[θ(i,j)][G(i+1,j)-G(i,j)]

(25)

(26)

(27)

(28)

(2)当90°≤θ<180°时，主要在第二、四象限中进行双线性插值，插值方法如图3所示。

图3 90°≤θ<180°时插值方法示意

在第二象限，梯度幅值线性插值：

Kup=α[G(i,j-1)+G(i-1,j-1)]+

|cos[θ(i,j)]|[G(i-1,j-1)-G(i,j-1)]

(29)

Kdown=α[G(i,j)+G(i-1,j)]+

|cos[θ(i,j)]|[G(i-1,j)-G(i,j)]

(30)

Kleft=α[G(i-1,j)+G(i-1,j-1)]+

|sin[θ(i,j)]|[G(i-1,j-1)-G(i-1,j)]

(31)

Kright=α[G(i,j)+G(i,j-1)]+

|sin[θ(i,j)]|[G(i,j-1)-G(i,j)]

(32)

Gx=Kdown+|sin[θ(i,j)]|[Kup-Kdown]

(33)

Gy=Kright+|cos[θ(i,j)]|[Kleft-Kright]

(34)

(35)

第四象限梯度幅值线性插值为

|cos[θ(i,j)]|[G(i+1,j+1)-G(i,j+1)]

(36)

|cos[θ(i,j)]|[G(i,j+1)-G(i,j)]

(37)

|sin[θ(i,j)]|[G(i,j+1)-G(i,j)]

(38)

|sin[θ(i,j)]|[G(i+1,j+1)-G(i,j+1)]

(39)

(40)

(41)

(42)

其中：相关系数α=0.5；cos[θ(i,j)]、sin[θ(i,j)]为比例函数，相当于自适应相关系数，所以设G(i,j)为目标像素的梯度幅值，根据G(i,j)的梯度方向θ上双线性插值得到G1(i,j)、G2(i,j)，当G(i,j)>G1(i,j)、G(i,j)>G2(i,j)时，G(i,j)为候选边缘极值点，否则为非边缘极值点，赋G(i,j)为0。在改进的非极大值抑制方法中，采用双线性插值的方法比较当前点与插值结果的点，用以判断是否为局部最大值，使得边缘的定位更加精确。

2.4 自适应双阈值理论求解

非极大值抑制后，须设定阈值进行边缘检测，根据日本学者OTSU的大隶法(最大类间方差)[17]中提出的两个评价函数：类间方差和类内方差。但是大多数的阈值边缘检测都是选择其中的一种来计算最佳阈值，本文作者利用2个评价函数的比值最大来寻求最佳双阈值。

经过非极大值抑制后梯度幅值分为L级，按模极大值大小分为C0、C1和C2三类：C0类为非边缘点的像素，C2类为边缘点的像素，C1类包含的像素可能是边缘点，也可能不是边缘点。设定ni为模数为i的像素的总数，pi为该模级像素数占整个图像像素的比例，灰度值出现的概率为

(43)

令C0包含模级[0,1,2,…,k]，C1包含模级[k+1,k+2,…,m]，C2包含模级[m+1,m+2,…,L-1]，则整副图像的总均值为

(44)

根据概率理论，各类出现的概率为

(45)

各类的均值为

(46)

根据概率理论，由各类的均值计算其类内方差为

(47)

类间最佳阈值评判函数为

(48)

最大类间方差反映的是各类之间的均衡性。

类内最佳阈值评判函数为

(49)

类内方差最小化反映的是每类像素之间的差别应当最小。

选取的最佳阈值应当是用该阈值分割得到的两类间具有最好的分离性，类间分离性最好的判据是数理统计意义上的类间特性方差最大或者类内特性方差最小，所以为兼顾类间和类内同时达到最优，提出采用类间最大方差与类内最小方差的最大比值作为最佳阈值，即：

(50)

多尺度小波变换自适应双阈值图像边缘检测具体步骤：(1) 构造计算小波滤波器参数；(2) 利用Mallat快速小波变换法[18-20]，在不同尺度j下，生成各层图像的梯度幅值fM2j(x,y)和相角fA2j(x,y)，尺度j=(1,2,…,J)；(3) 根据各层梯度幅值fM2j(x,y)对应的相角fA2j(x,y)在相应的象限中进行双线性插值求极大幅值，非极值幅值赋0，生成各层可能的边缘图像p2j(x,y)；(4) 采用文中双自适应阈值对各层可能的边缘图像p2j(x,y)进行筛选，得到各层边缘图像D2j(x,y)； (5) 从最大尺度层j开始，对该层的每一个边缘点在下一层j-1中以这点为中心对应的3×3领域内，查找可能的候选边缘点，根据幅值相近、相角相似链接候选边缘点，删除离散点，得到j-1尺度下的边缘图像D2j-1(x,y)；(6) 依次循环步骤(5)直到最后尺度j=1，得到多尺度融合的边缘图像E(x,y)。

3 水下焊缝图像边缘检测实验对比与结果分析

3.1 实验设备

该实验设备实物如图4所示，主要由上位机控制器、模拟焊缝板、水箱、双目摄像机组成。

图4 水下双目视觉系统实验平台

3.2 焊缝图像边缘检测实验

根据现实工作环境水质的不同，分别对清水和浑浊水中的焊接板采集图像，利用几种常用边缘检测算法及文中方法分别对这2种情况水下焊缝图像进行边缘检测，结果分别如图5、6所示。

图5 3种算法分别对清水下焊缝图像进行边缘检测比较

由图5—图6可以看出：在2种不同水质环境下进行焊缝边缘检测，文中改进方法比其他2种算子检测效果更佳、更准确、更完整，并且能有效滤除各种噪声产生的伪边缘，为水下焊接自动跟踪定位提供了条件，其他2种算法滤除噪声的同时也弱化了边缘信息，这表明文中改进算法是正确可行的，体现了多尺度小波变换对图像处理的优越性。

图6 3种算法分别对浑浊水下焊缝图像进行边缘检测比较

4 结论

本文作者针对水下焊缝图像受到漂浮颗粒、泥沙、弧光、飞溅、水浑浊等因素的噪声影响而难以检测并提取出准确完整的焊缝边缘，分析了传统Canny算子存在的缺点，提出了一种改进Canny边缘检测算法，引入了多尺度小波变换，采用双线性插值优化非线性极大值抑制，并结合OTSU法生成自适应双阈值，对水下焊缝图像进行焊缝边缘检测。结果表明：改进后的算法正确可靠，可以抑制噪声，且能较快检测出准确清晰完整的焊缝边缘，有效滤除伪边缘，为实现水下焊接机器人自动跟踪焊缝提供了可靠的焊缝图像边缘信息。