燃油泵齿轮受力分析及其近似计算方法

顾广溪，郭垠昊，王峥嵘

(1.新乡航空工业(集团)有限公司103厂，河南新乡 453003;2.陆军装备部航空军事代表局驻洛阳地区航空军事代表室,河南洛阳 471000;3.兰州理工大学能源与动力工程学院，甘肃兰州 730050)

0 前言

外啮合斜齿轮泵结构简单、工作可靠、自吸性能好、抗污染性强[1]，在航空发动机燃油系统中得到了广泛应用，作为提供燃油的主要动力源，其性能优劣直接影响燃油系统的性能[2]。工作过程中，齿轮除在啮合力和液压力的作用下受到不平衡径向力外，还因螺旋角的存在受到一定的轴向力，容易导致齿轮轴变形加大、轴承及端盖磨损严重等问题。因此，如何精确得到外啮合斜齿齿轮泵工作过程中齿轮所受径向力大小及方向和轴向力大小，对此类泵的优化设计具有重要意义。

针对外啮合齿轮泵径向力，研究人员从不同角度展开了研究。文献[3]通过Fluent流场仿真分析和理论简化计算方法，推导了主、从动齿轮上的径向力公式并提出了两项减小径向力的措施。文献[4]将主动齿轮分为高压区、低压区、过渡区和啮合区，对每个区域齿轮所受径向力进行了理论分析，并采用PumpLinx进行了仿真验证。文献[5]提出一种利用困油力抵消部分径向力的方法和一款浮动侧板内侧面上的实施结构。文献[6-7]基于Pro/E和Fluent流场分析软件分析了卸荷槽改进前后外啮合齿轮泵径向力的变化规律，研究发现合理设计卸荷槽可有效降低齿轮泵的不平衡径向力。文献[8]针对传统齿轮泵不平衡径向力使得轴承磨损加剧的问题，提出将谐波齿轮传动技术与内啮合齿轮泵结合形成谐波式齿轮泵。文献[9]利用ADINA软件对水压外啮合齿轮泵内部流场进行了仿真分析，在此基础上分析了齿轮泵内液压径向力的大小和方向。文献[10]考虑全齿廓曲线的受力情况，在MATLAB软件中采用Quadgk函数对外啮合齿轮泵的齿轮径向力进行了数值计算。文献[11]研究了具有扩大高压区结构的外啮合齿轮泵的径向力和传动扭矩的计算公式。文献[12]针对传统齿轮泵存在径向力不平衡、排量小、流量脉动大等问题，借鉴双作用叶片泵原理提出了一种双作用齿轮泵。此外，文献[13]利用CFD软件分析了外啮合齿轮泵的轴承受力情况进而对轴承进行了优化设计；文献[14]通过研究外啮合齿轮泵输出流量以及从动轮所受液压力与平衡槽的关系，对齿轮泵侧板平衡槽进行了优化设计。综上，现有关于外啮合齿轮泵径向力的理论计算方法往往是在一定的简化条件下提出的，而仿真分析通用的CFD软件[15-17](Fluent、CFC、STAR-CD等)对齿轮泵的仿真通常局限于二维或三维放大间隙的简化模型。

本文作者以某型燃油泵为研究对象，采用PumpLinx软件仿真得到主、从动齿轮所受液压力矩的精确值，进而计算齿轮所受啮合力和液压力，最终获得不同工况下齿轮所受径向力大小和方向以及轴向力大小，最后通过数据拟合提出一种外啮合斜齿齿轮泵齿轮受力的近似计算方法。

1 某型燃油泵及其齿轮主要参数

某型燃油泵为外啮合齿轮泵，其转速范围为2 400～8 000 r/min，进口最大压力为1.2 MPa，出口最大压力为4.17 MPa，采用斜齿圆柱齿轮，主动齿轮和从动齿轮安装中心距为30 mm。主动齿轮螺旋角采用右旋，从动齿轮为左旋。齿轮的主要参数如表1所示。

表1 某型燃油泵主动齿轮主要参数

2 低速工况下燃油泵齿轮受力分析

2.1 主、从动齿轮所受液压力矩

根据表1中的参数建立某型燃油泵主动齿轮和从动齿轮的三维模型。以端面上一对齿形处于啮合中间位置为齿轮转角的零点，基于PumpLinx软件对该齿轮泵工作时主、从动齿轮的液压力矩进行仿真计算。在泵转速2 400 r/min、进口压力1.2 MPa、出口压力2.01 MPa工况下，主动齿轮和从动齿轮所受液压力矩及其合力矩如图1所示。

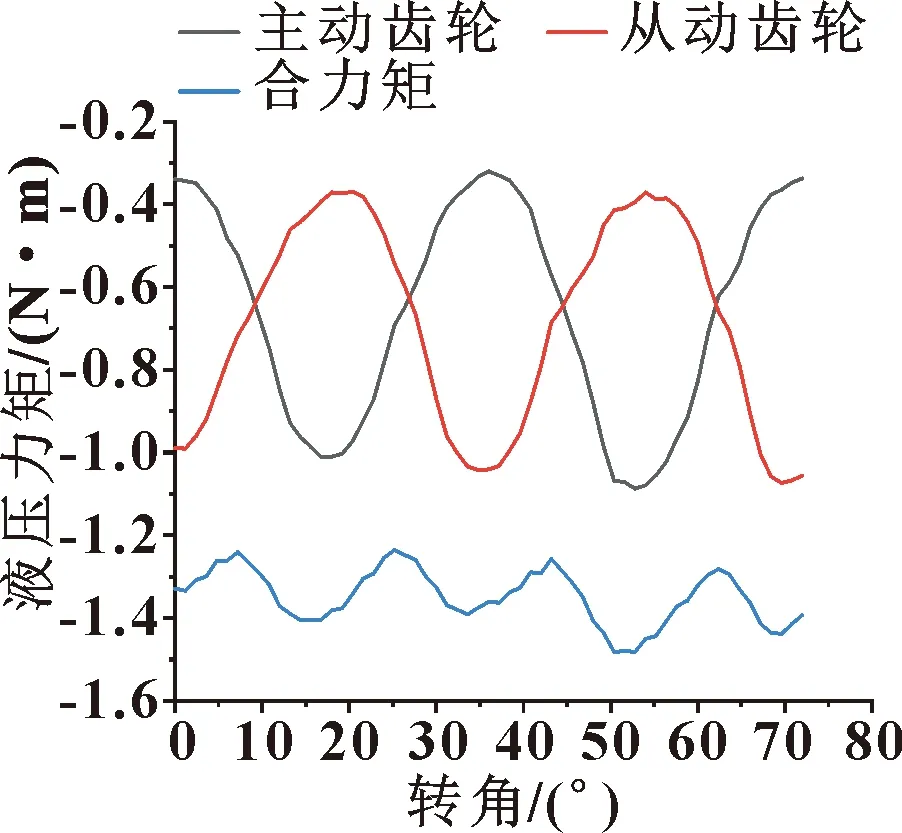
图1 主、从动齿轮所受液压力矩及其合力矩

由图1可知：主、从动齿轮所受液压力矩绝对值在0.3～1.1 N·m间变化，合力矩绝对值在1.26～1.46 N·m之间变化。主动轴输入力矩主要克服主动齿轮和从动齿轮所受的液压力矩以及机械密封的摩擦损失、滑动轴承的机械损失、齿轮旋转的黏性摩擦损失、齿轮传动的机械摩擦损失等力矩。泵转速2 400 r/min、空载时，试验测得输入扭矩为0.8 N·m(限于篇幅和保密需要，此处未给出试验介绍，仅给出试验数据)，此力矩用于克服上述各种摩擦损失力矩；当泵出口压力为2.01 MPa时，试验测得轴的输入扭矩为2.2 N·m，则这两种工况下泵轴的输入扭矩差(1.4 N·m)即为齿轮转动时克服主动齿轮和从动齿轮所受液压力矩所需扭矩。图1中主、从动齿轮所受液压合力矩的仿真结果与试验测量结果计算差值基本一致，表明了仿真结果的正确性。

2.2 斜齿轮传动啮合力计算

斜齿轮啮合时齿轮所受圆周力、轴向力和径向力如图2所示。

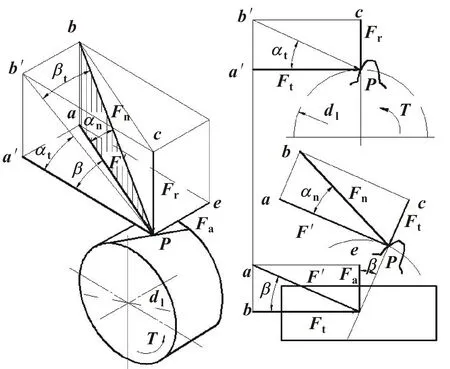
图2 斜齿轮啮合力分布简图

斜齿轮泵工作时，为实现平稳传动和高低压腔封油，任意时刻均有2对及以上齿处于啮合状态，转角不同，啮合点到齿轮轴支撑中心的距离不同，但各对啮合齿啮合点到齿轮中心距离的平均值基本不变。为方便计算，取从动齿轮啮合力矩的力臂为齿轮啮合节圆的半径d’，则齿轮所受圆周力Ft、轴向力Fa以及径向力Fr与齿轮间传递的扭矩T间的关系如式(1)所示：

(1)

由表1和表2中的数据以及式(1)可得在泵转速2 400 r/min、进口压力1.2 MPa以及出口压力2.01 MPa工况下，齿轮所受圆周力、轴向力和径向力如图3所示。

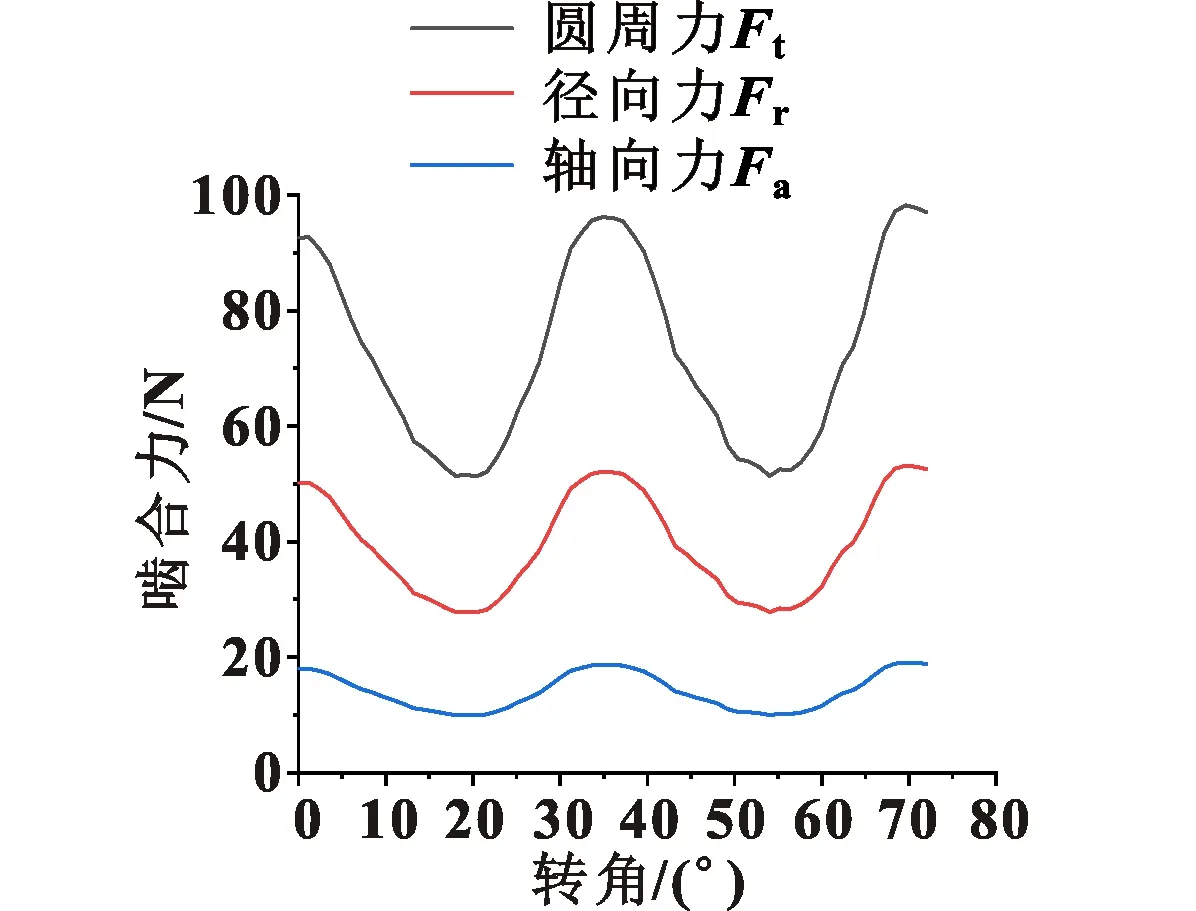
图3 低速工况齿轮啮合力

2.3 主、从动齿轮液压力

为便于计算斜齿轮所受液压力及合力，建立如图4所示的参考坐标系。其中，z轴沿泵轴轴线方向。对仿真得到的齿轮表面各处压力进行面积积分，可得主动齿轮和从动齿轮所受x向、y向和轴向(z)液压力如图5所示。

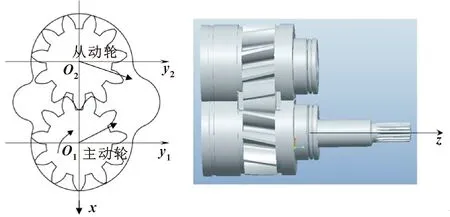
图4 主、从动齿轮受力参考坐标系

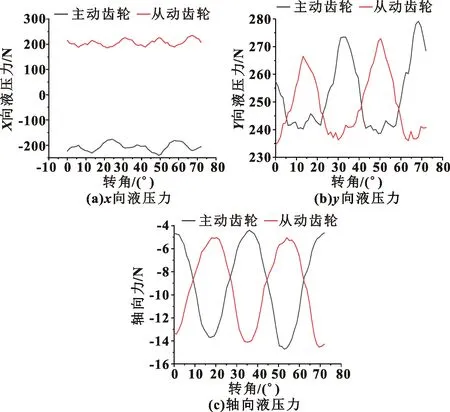
图5 低速工况主、从动齿轮所受液压力

2.4 主、从动齿轮所受合力

分别在x向、y向和z向对齿轮所受液压力和啮合力进行叠加即可得主动齿轮和从动齿轮在各方向的合力，即：

(2)

(3)

式中：Fz,x、Fz,y1和Fz,z分别表示主动齿轮在x向、y向和z向所受合力；Fyz,x、Fyz,y和Fyz,z分别表示主动齿轮在x向、y向和z向所受液压力；Fc,x、Fc,y2和Fc,z分别表示从动齿轮在x向、y向和z向所受合力；Fyc,x、Fyc,y和Fyc,z分别表示从动齿轮在x向、y向和z向所受液压力。

从而可得主动齿轮和从动齿轮的径向力合力分别为

(4)

式中：Fz,j和Fc,j分别表示主动齿轮和从动齿轮的径向力合力，其方向分别由arctan(Fz,x/Fz,y1)和arctan(Fc,x/Fc,y2)决定。

将图3、图5中齿轮啮合力和所受液压力代入式(2)—式(4)可得主、从动齿轮的径向合力、径向合力与y轴夹角、轴向力大小如图6所示。

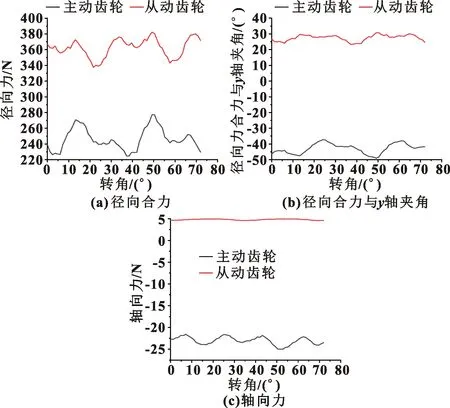
图6 低速工况主、从动齿轮所受合力

3 变工况下燃油泵齿轮受力分析

由前述仿真分析和理论计算方法，得到不同工况下齿轮所受液压合力矩如表2所示。可见：在变工况下，仿真值与试验测量结果也基本吻合。

表2 变工况下齿轮液压合力矩的仿真平均值和试验值

由式(2)—式(4)，得变工况下主、从动齿轮受到的径向合力、径向合力方向及轴向力如图7所示。

图7 变工况下主、从动齿轮受力

4 燃油泵齿轮受力近似计算方法

泵进出口压差是齿轮受力的主要影响因素，变工况下，主动齿轮和从动齿轮所受平均径向力以及主动齿轮所受平均轴向力与泵进出口压差之间的关系如图8—图9所示。

由图8—图9可以看到：主、从动齿轮所受平均径向力和轴向力随进出口压差近似线性变化。经数据拟合，主动齿轮和从动齿轮所受径向力以及主动齿轮所受轴向力可用经验公式(5)计算，各力的计算值和经验公式的拟合值基本吻合。

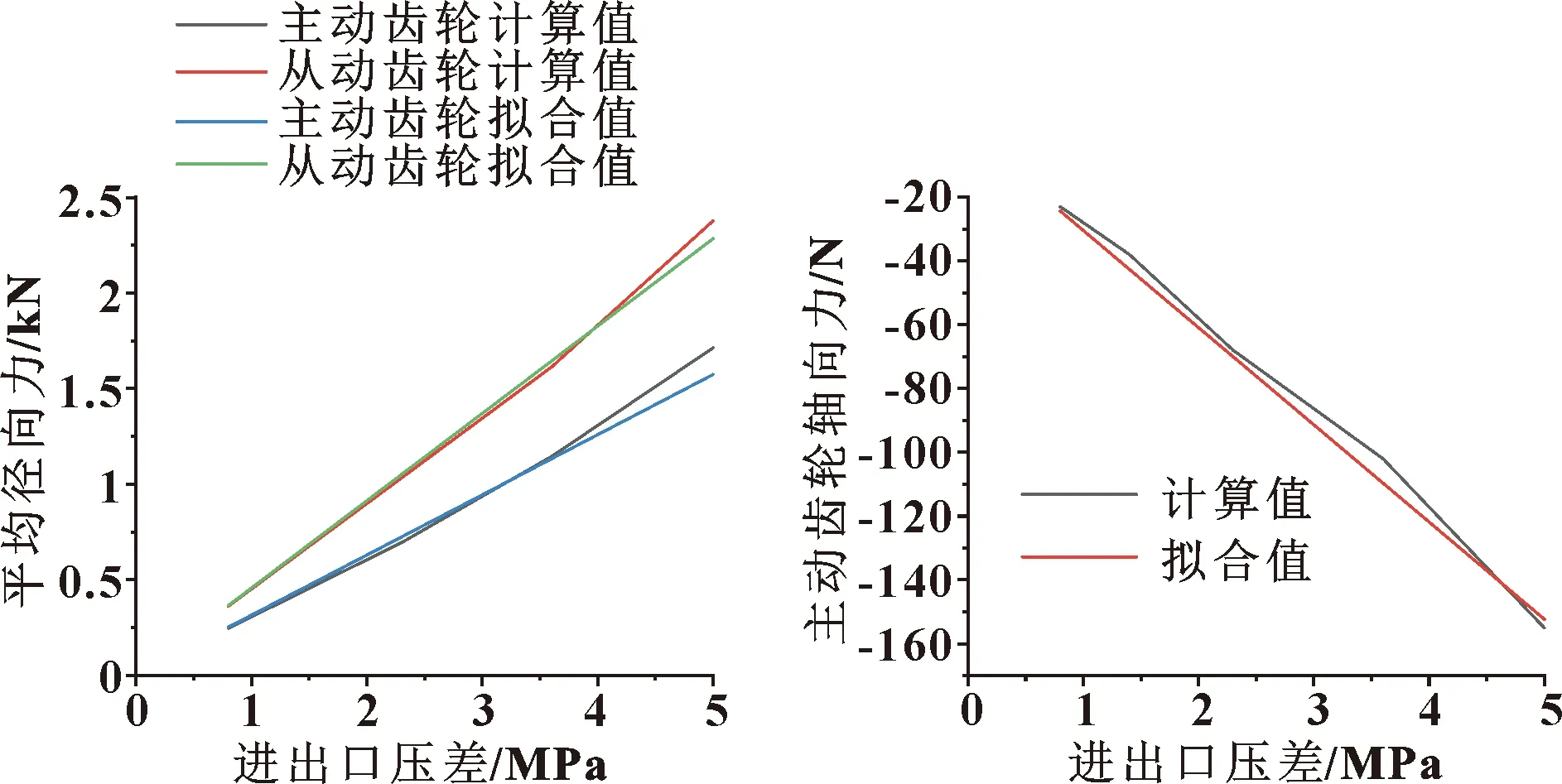
图8 主、从动齿轮径向力随压差变化的计算值和拟合值 图9 主动齿轮轴向力随压差变化的计算值和拟合值

(5)

式中:Δp为泵进出口压差；B为齿轮齿宽；da为齿轮齿顶圆直径。

5 结论

(1) 基于PumpLinx仿真软件获得了某型燃油泵在变工况下主动齿轮和从动齿轮受到的液压力矩，在此基础上结合齿轮传动啮合力的理论计算公式得到了泵啮合力的准确值，并通过叠加齿轮所受液压力和啮合力得到了主、从动齿轮径向合力大小及方向、轴向力随齿轮转角的变化情况，为外啮合斜齿齿轮泵滑动支撑轴承的设计与校核提供了参考。

(2) 在不同进出口压差下，分析了某型燃油泵主动齿轮和从动齿轮的径向合力以及主动齿轮轴向力的大小，进而给出了主、从动齿轮的径向力以及主动齿轮的轴向力关于泵进出口压差、齿宽和齿顶圆直径的经验公式，为系列泵齿轮的受力分析提供了一种近似计算方法。