宏微3-RPR并联机构运动学精确求解
2022-12-29许有熊顾人杰刘晓锋朱松青
许有熊, 顾人杰, 刘晓锋, 朱松青
(1.南京工程学院自动化学院,江苏南京 211167;2.国电南京自动化股份有限公司, 江苏南京 211000)
0 前言
随着现代科学技术的不断发展,精密加工与精密测量、航空航天、微电子工程等领域对并联机构的运动范围和精度提出了更高的要求[1]。但是,目前并联机构不能同时满足大范围和高精度运动的要求。例如,液压伺服、电机伺服等驱动的并联机构能实现大范围运动,但其重复定位精度一般为微米级,不能实现高精度[2-3];压电陶瓷[4]为驱动的并联微动机构能实现较高的定位精度,但其运动范围较小[5]。这极大限制了并联机构在精密工程领域的应用。
因此,国内外学者将宏微混合驱动技术[6-7]应用到并联机构,研究混合驱动的并联机构以解决大范围和高精度之间的矛盾。华南理工大学的余竞[8]研究了一种宏微平面3-RRR并联机构系统,其中,宏动部分采用伺服电机驱动的平面3-RRR并联机构,并在其动平台上放置一个由压电陶瓷驱动的3-RRR平面并联微动机构,以保证系统的定位精度,但该结构较复杂,且定位精度尚未达到纳米级,尚未达到实际应用。结合液压伺服技术与压电技术的优点应用到并联机构中,文献[9]提出了一种基于电液-压电混合伺服驱动的3-RPR并联机构,能有效实现大范围高精度定位。
另外,从并联机构的运动学来看,国内外相关学者都进行了研究,并取得了一些成果。比如并联机构运动学分析的核心问题是建立并求解高维非线性代数方程组,目前其基本方法主要有两大类,即Sylvester结式消元法、Groebner基法、吴文俊消元法等代数解析法以及优化法,Newton-Rapgson法等数值迭代法,但以上方法求解精度都无法达到纳米级。
因此,本文作者在之前研究的基础上[9],探索研究宏微3-RPR运动学精确求解,以满足后续大范围和高精度定位的控制要求。
1 宏微3-RPR并联机构工作原理
所提出的宏微混合伺服驱动3-RPR并联机构原理如图1所示。
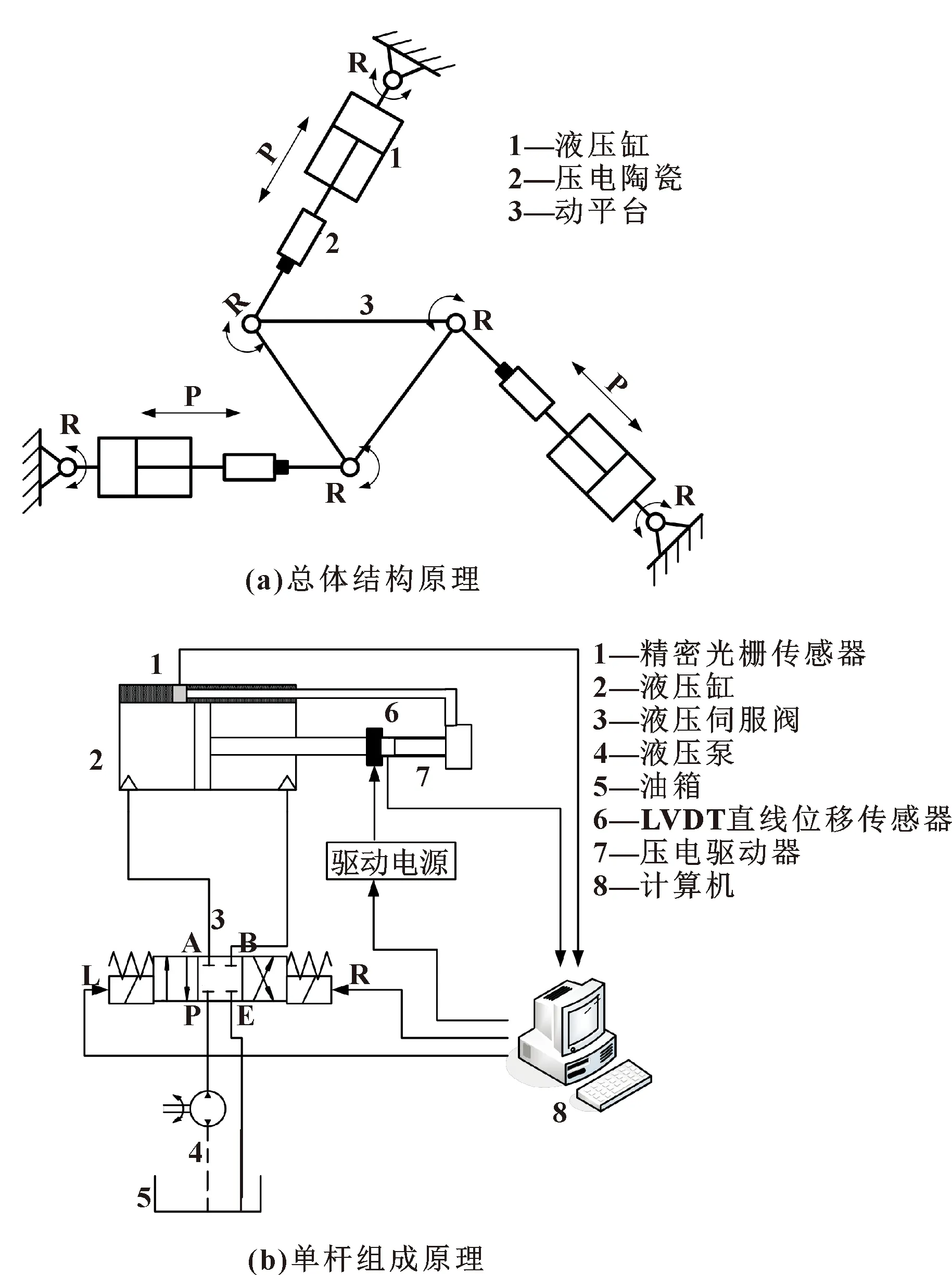
图1 宏微3-RPR结构原理
其中每个杆由液压缸和压电陶瓷驱动器串联而成,如图1 (b)所示,并通过控制3个杆伸缩的总长度来控制动平台的平动和转动。宏驱动部分采用电液伺服系统以实现大范围运动,微驱动部分采用压电陶瓷驱动器以实现高精度精密定位。
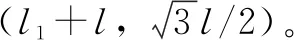
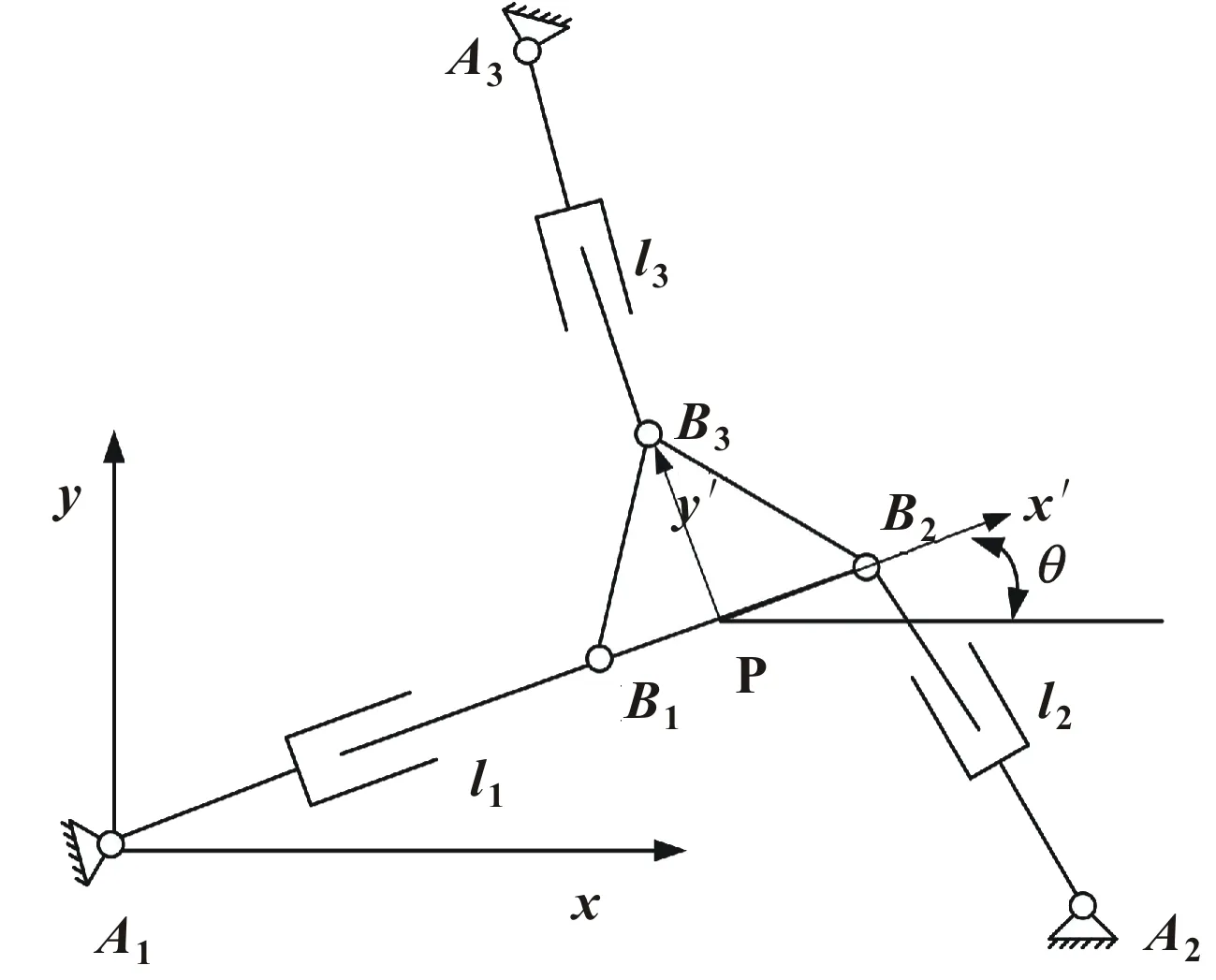
图2 3-RPR的结构参数示意
2 运动学逆解分析
运动学逆解是通过已给定的动平台位姿(x,y,θ),求解各杆的运动量(l1,l2,l3)。相对串联机构而言,并联机构的运动学逆解较为简单,可以直接求解。假设初始状态下每根杆长为均为L,θ=0,则可得出A、B、C各点坐标为
A:(0,0)
当机构运动到一定位置时,设此刻偏转角度为θ,动平台中心点坐标为(x,y)可得
点B1坐标为
点B2坐标为
点B3坐标为
由此可得逆解的方程组为
(1)
采用MATLAB编程实现其运动学逆解,其求解程序截图如图3所示。

图3 逆解程序截图
3 运动学正解分析
(1)数值迭代法的求解分析
运动学正解是已知各杆的运动量(l1,l2,l3),求解动平台的位姿量(x,y,θ)。其运动学正解的方程组如式(2)所示:
(2)
其中:x1、x2分别为sinθ、cosθ。
由于并联机构运动学正解的复杂性,很难求出方程的解析解,通常使用数值迭代法进行求解。其计算过程可简述为
(1)初选x0;
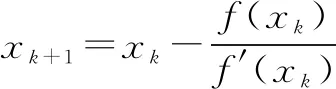
采用MATLAB编程实现其数值迭代法的求解,主要包含3个部分程序,即原方程组程序、求导程序和迭代程序。其中数值迭代法的迭代程序截图如图4所示。

图4 正解程序截图
(2)BP神经网络的求解分析
采用上述数值迭代法求解时,所需的计算时间较长,且在计算过程中对初值选取要求过高,同时在导数为0处会产生奇异现象,其求解精度也无法满足纳米级的计算要求。因此,采用BP神经网络算法进行宏微3-RPR并联机构运动学正解。
BP神经网络是一种由输入层、隐藏层和输出层组成的多层前馈神经网络[10-11]。事先给定输入数据组和目标数据组,通过神经网络训练,得到每次训练的结果,与目标结果进行误差比较,并根据误差反向传播修改权值和阈值,重复该过程直到获得能输出和目标结果一致的模型。
根据所研究宏微3-RPR运动学数据模型,以各杆的运动量(l1,l2,l3)为输入,动平台的位姿(x,y,θ)为输出,建立一个三输入三输出的神经网络架构,为提高精度,隐藏层节点数设为100,如图5所示。
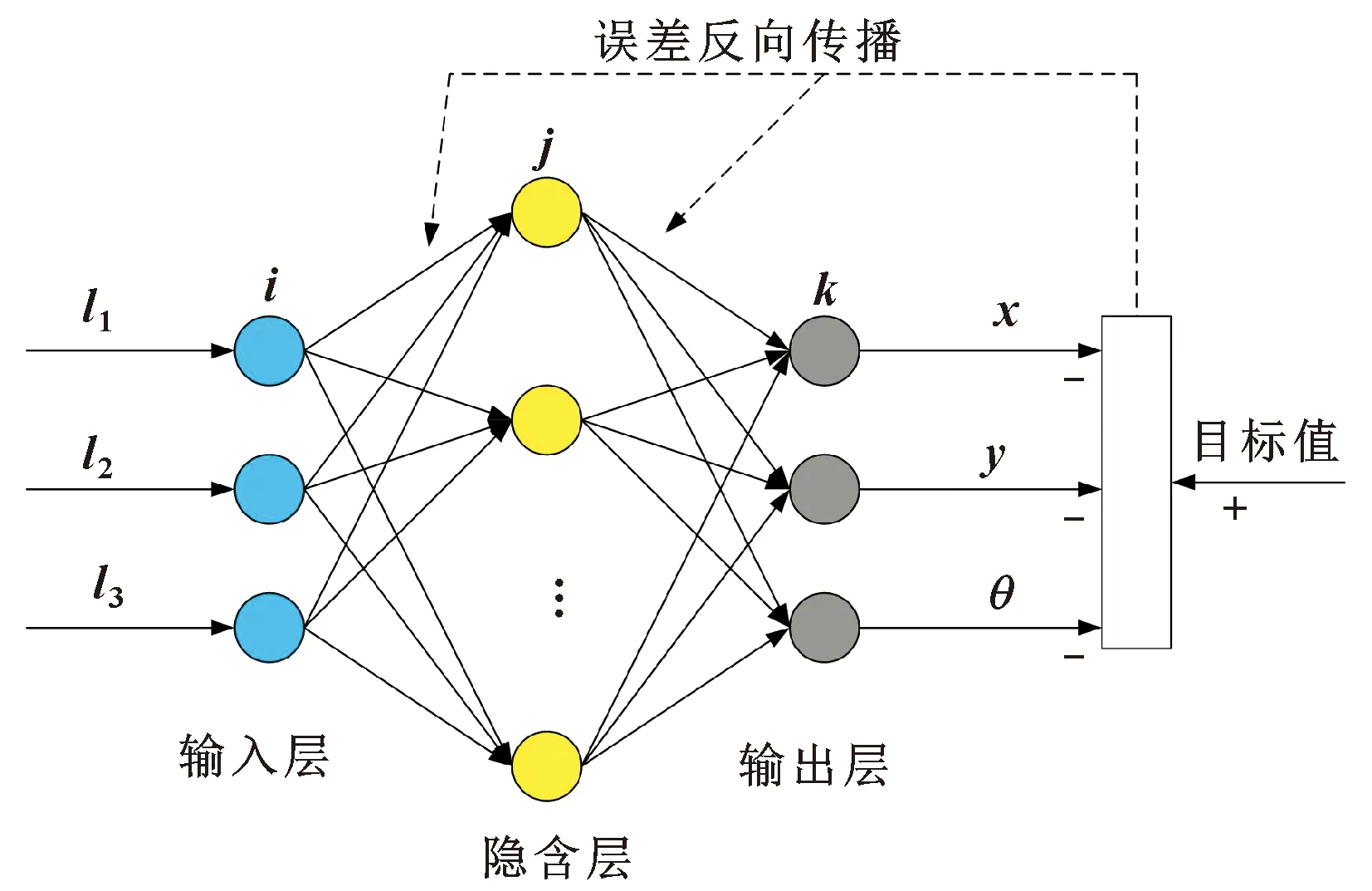
图5 BP神经网络算法结构示意
其过程为:首先,对并联机构利用式(1)进行运动学逆解,将逆解得到的结果作为训练样本的输入值,逆解的输入值作为BP网络的期望输出值;其次,采用BP算法对样本进行训练,求得3-RPR并联机构运动学正解的神经网络模型;最后,通过另一组数据验证神经网络模型的准确性。神经网络算法训练结果如图6所示。

图6 BP神经网络算法训练
由于输入输出量的取值范围不同,会降低神经网络的训练精度和训练速度,因此在训练之前需要先对数据库进行归一化处理,并在训练结束后进行反归一化处理。
(3)遗传算法优化的神经网络算法
虽然BP神经网络得到了广泛的应用,但因其初始权值和阈值选取的随机性,难以选取到较合适的值,因此BP神经网络存在训练时间较长、计算误差较大、容易陷入局部最优解等不足。如图6所示的神经网络算法在计算次数为2×106次时,耗时79 h。基于上述缺点,采用遗传算法优化的BP神经网络算法进行并联机构运动学正解分析。
遗传算法是一种通过模拟自然生物进化过程搜索最优解的方法[12]。其基本计算过程为:首先初始化一个种群,计算各个体的适应度;然后根据“优胜劣汰,适者生存”的原理,进行选择、交叉、变异等操作得到下一代群体,不断提高其适应度;直至满足一定条件,将具有最大适应度个体作为最优解输出。
因此,采用遗传算法对神经网络算法的权值选取过程进行优化[13],既能缩短训练时间,提高网络收敛速度,又可以有效避免训练中陷入局部最优解,其原理如图7所示。
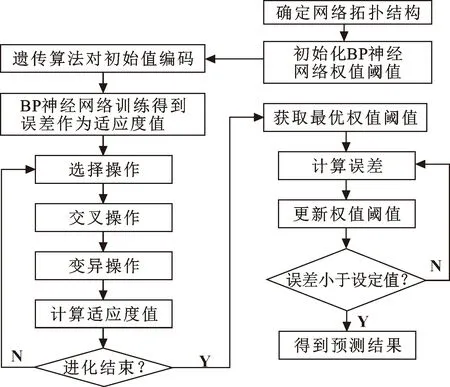
图7 遗传算法简要原理
基于MATLAB软件的遗传算法优化的BP神经网络算法训练结果如图8所示。将BP神经网络算法和遗传算法优化的BP神经网络训练过程进行对比,如图9所示。可以看出:在经历相同次数的训练后,遗传算法优化的神经网络算法精度远远高于BP神经网络。在相同精度下,遗传算法优化的神经网络算法耗时会更短。

图8 遗传算法优化的神经网络算法训练
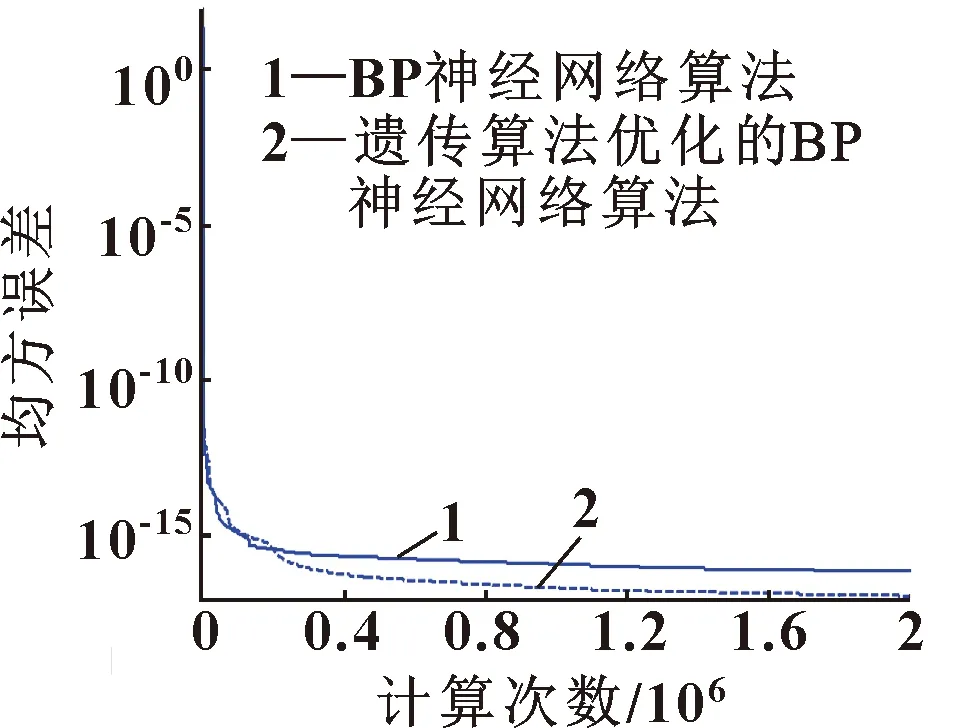
图9 2种算法对比
将不同算法得到的逆解进行对比分析,得到表1,其计算误差如表2所示。可以看出:牛顿迭代法的精度在微米级,BP神经网络算法的精度在0.1微米级,遗传算法优化的神经网络算法的精度在纳米级。这说明遗传算法优化的神经网络算法精度最高,满足计算要求。
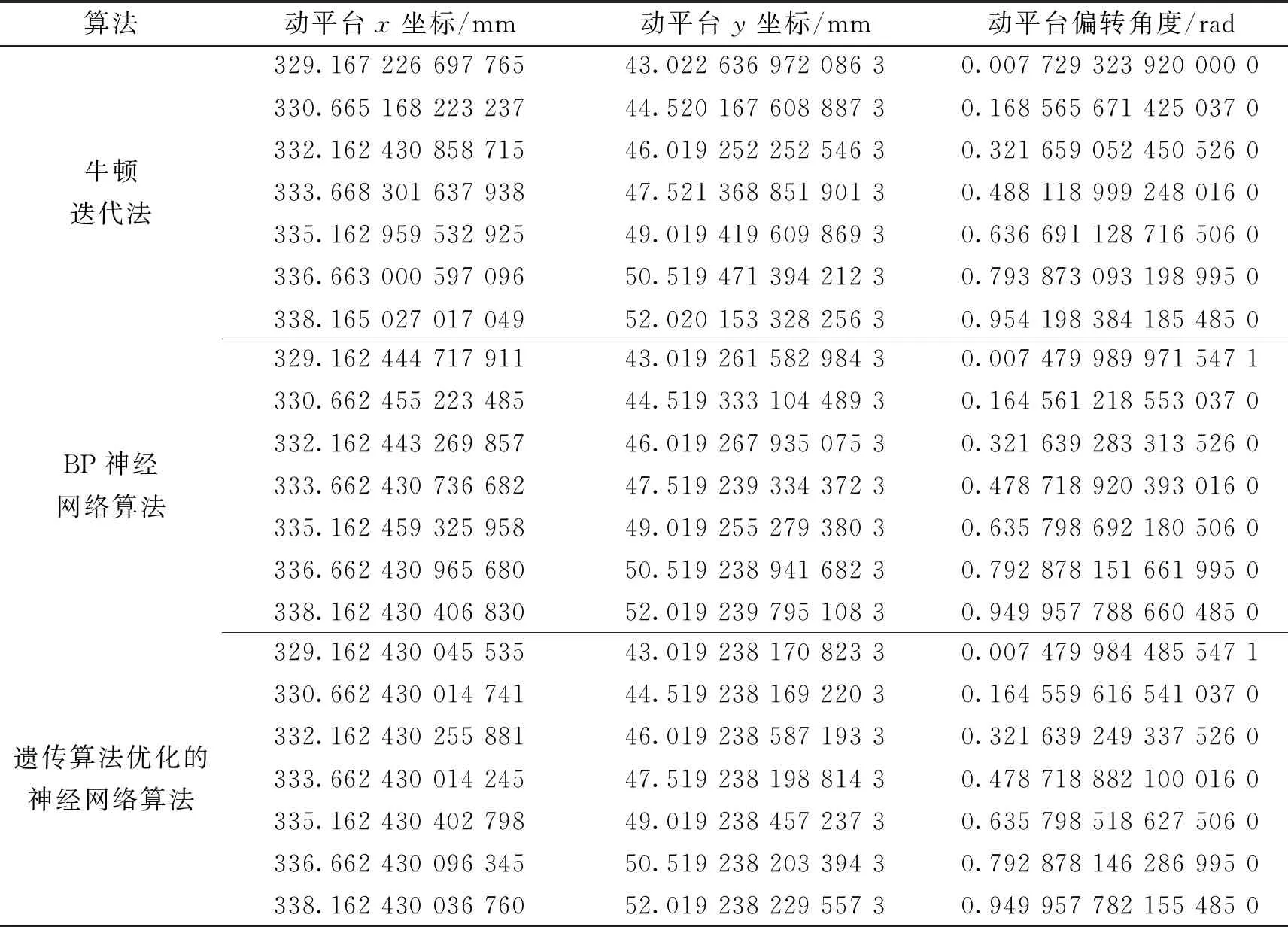
表1 不同算法计算下的运动学正解值

表2 不同算法下的误差比较
4 结论
根据先前所研究的宏微混伺服驱动的3-RPR并联机构纳米级控制精度的要求,要求其运动学求解精度也要达到纳米级,文中对它进行运动学精确求解研究。
(1)建立了宏微3-RPR运动学模型,并采用MATLAB编程实现其运动学逆解,得到其准确解作为后续运动学正解的训练样本数据。
(2)分别采用数值迭代法、神经网络算法和遗传算法优化的神经网络算法进行并联机构的运动学正解研究。
通过最终的求解精度对比,经遗传算法优化的神经网络算法能实现纳米级的求解精度且耗时更短。这为后续并联机构的控制奠定基础。
