Global Well-Posedness of Solutions to 2D Prandtl-Hartmann Equations in Analytic Framework

DONG Xiaoleiand QIN Yuming

1 College of Information Science and Technology, Donghua University, Shanghai 201620,China.

2 Department of Mathematics,Donghua University,Shanghai 201620,China.

3 Institute for Nonlinear Science,Donghua University,Shanghai 201620,China.

Abstract. In this paper, we consider the two-dimensional (2D) Prandtl-Hartmann equations on the half plane and prove the global existence and uniqueness of solutions to 2D Prandtl-Hartmann equations by using the classical energy methods in analytic framework. We prove that the lifespan of the solutions to 2D Prandtl-Hartmann equations can be extended up to Tε(see Theorem 2.1)when the strength of the perturbation is of the order of ε. The difficulty of solving the Prandtl-Hartmann equations in the analytic framework is the loss of x-derivative in the term v∂yu. To overcome this difficulty,we introduce the Gaussian weighted Poincar´e inequality(see Lemma 2.3).Compared to the existence and uniqueness of solutions to the classical Prandtl equations where the monotonicity condition of the tangential velocity plays a key role,which is not needed for the 2D Prandtl-Hartmann equations in analytic framework. Besides,the existence and uniqueness of solutions to the 2D MHD boundary layer where the initial tangential magnetic field has a lower bound plays an important role, which is not needed for the 2D Prandtl-Hartmann equations in analytic framework,either.

Key Words: Prandtl-Hartmann;existence and uniqueness;energy method;analytic space.

1 Introduction

The following Prandtl-Hartmann equations were derived in [1] by the classical two dimensional (2D) incompressible MHD system under a transverse magnetic field on the boundary for the parameters of the system in the mixed Prandtl-Hartmann regime. In this paper, we shall investigate the global existence and uniqueness of solutions to the following initial boundary value problem for the 2D Prandtl-Hartmann system on the upper half plane R2+={(x,y):x∈R,y∈R+},which reads as

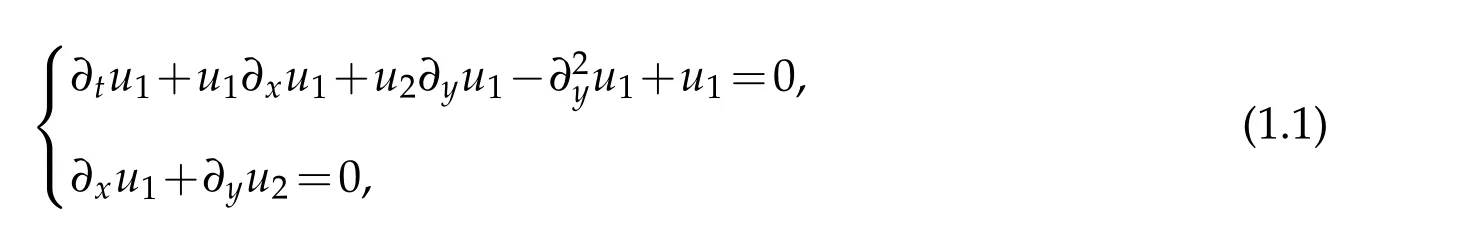
where the velocity field(u1(t,x,y),u2(t,x,y))of the boundary layer is an unknown vector function.

The system(1.1)is subject to the initial data and boundary conditions

The far field is represented by a positive constant ¯u,where

To start with,let us briefly review some known results to the problem(1.1).Especially,when the damping termu1does not exist,the system(1.1)reduces to the classical Prandtl equations which was firstly introduced formally by Prandtl [2] in 1904. This system is the foundation of the boundary layer equations. It describes that the part away from the boundary can be considered as general ideal fluid, but the part near a rigid wall is deeply affected by the viscous force. Formally,the asymptotic limit of the Navier-Stokes equations can be denoted by the Prandtl equations within the boundary layer and by the Euler equations away from boundary. About sixty years later,Oleinik[3]established the first systematic work in strictly mathematic analysis, in which she pointed out that the local-in-time well-posedness of Prandtl system can be proved in 2D by using the Crocco transformation under the monotonicity condition on the tangential velocity field in the normal variable to the boundary. This result together with an expanded introduction to the boundary layer theory was showed in Oleinik-Samokhin’s classical book[4].

There have been some results in the analytic framework with analytic radiiτ(t) for 2D boundary layer equations. First,authors[5]investigated the local well-posedness of solutions to the 2D Prandtl and hydrostatic Euler equations by energy methods, which was the original result for boundary layer problem in the analytic framework with analytic radiiτ(t). Kukavica and Vicol[6]considered the local well-posedness of solutions to the 2D Prandtl boundary layer equations with general initial data by using analytic energy estimates in the tangential variables. Later on, Ignatova and Vicol [7] investigated the almost global existence for the two-dimensional Prandtl equations when the small initial datum lies in an exponential weighted space by applying analytic energy estimates in the tangential variables and proved that the unique solution extended at least up toTε≥exp(ε−1/log(ε−1)). To be more precise,our motivation in this paper is to use energy method to prove the global existence and uniqueness of solutions to 2D Prandtl-Hartmann equations, which is still an open problem in analytic framework before the present paper solved it.

There also have been a lot of results for the 2D Prandtl equation in different frameworks, for example, weighted Sobolev space framework and Gevery framework, etc.Under the Oleinik′s monotonicity assumption, some authors [8–10] proved the wellposedness of solution for 2D Prandtl equations by using energy method and constructing a new unknown function to eliminate the troublesome term from the convection term.In addition to Oleinik′s monotonicity assumption on the tangential velocity field, Xin and Zhang[11]obtained the existence of global weak solutions to the Prandtl equation when the pressurepis favourable (i.e.,∂xp≤0). Qin and Wang [12] investigated the global existence of solutions to 2D magnetic Prandtl model in the Prandtl-Hartmann regine by energy method. So far, besides the well-posedness of solutions to Prandtl equation in weighted Sobolev space, there are many results about the existence theory of solutions,for example,authors in[13–18]investigated the well-posedness of the Prandtl equations for the initial data in Gevrey framework. There also have been some results for the Prandtl equations by using the methods which are different from energy method. For interested readers,we refer to[19–23]and the references therein for the recent progress.

Motivated by[7,24],we investigate the global well-posedness of solutions to two dimensional Prandtl-Hartmann equations(1.1)-(1.3)in the analytic framework by standard energy methods. The proof of the global well-posedness of solutions is divided into two sections. First,we prove the existence of solutions for equations(1.1)-(1.3) by using the classical energy method. The difficulty of solving the problem (1.1)-(1.3) in the analytic framework is the loss ofx-derivative in the termv∂yu. To overcome this difficulty, we show the Gaussian weighted Poincar´einequality (see Lemma 2.3). In other words, the Poincar´einequality does not holds in unbounded domains. Then, similar to the estimates of the existence of solutions, we verify the uniqueness of solutions for equations(1.1)-(1.3)as usual.Compared to the existence and uniqueness of solutions to the classical Prandtl equations where the monotonicity condition of the tangential velocity plays a key role, which is not needed for the 2D Prandtl-Hartmann equations (1.1)-(1.3) in analytic framework.Besides,the existence and uniqueness of solutions to the 2D MHD boundary layer where the initial tangential magnetic field has a lower bound plays an important role, which is not needed for the 2D Prandtl-Hartmann equations (1.1)-(1.3) in analytic framework,either.

It is noteworthy that the above results are mainly devoted to the two-dimensional Prandtl equations and there also have been some results for the three-dimensional Prandtl equations,see[25–30]. For general MHD equations,there have been some results in the analytic framework. Xie and Yang[31]studied the global existence of solutions to the 2D MHD boundary layer equations in the mixed Prandtl and Hartmann regime when initial datum is a small perturbation of the Hartmann profile, and obtained that the solution in an analytic norm is an exponential decay in time. Recently,Liu and Zhang[32]established the global existence and the asymptotic decay estimate of solutions to the 2D MHD boundary layer equations with small initial data.Inspired by[7],Xie and Yang[24]investigated the lifespan of solution to the 2D MHD boundary layer system by using the cancellation mechanism and obtained the lifespan of solution has a lower bound. Motivated by[6],Lin and Zhang[33]studied the local existence of solutions for 2D incompressible magneto-micropolar boundary layer equations when the initial data are analytic in thexvariable by using energy methods. There also have been some results for the MHD equations by using the methods which are different from energy method. For interested readers,we refer to[34–39]and the references therein for the recent progress. So far,besides the well-posedness of solutions in the frameworks of Sobolev and analyticity,there also have been some results on the vanishing limits[40–42]for the MHD equations.

Finally, the rest of the paper is arranged as follows. In Section 2, we show the main result in this paper and give some lemmas which will be used frequently.In Section 3,we prove the existence of solutions for Eqs. (1.1)-(1.3)by using the classical energy method.In Section 4, we verify the uniqueness of solutions for Eqs. (1.1)-(1.3) and complete the proof of Theorem 2.1. We will complete the proof of Theorem 2.1 by a series of lemmas and it will be done by some inequalities in[43–45].

Hereafter,let letterCbe a general positive constant,which may vary from line to line at each step.

2 Main result

As in[7,24],we use the following Gaussian weighted functionθαto introduce the function space of the solutions,

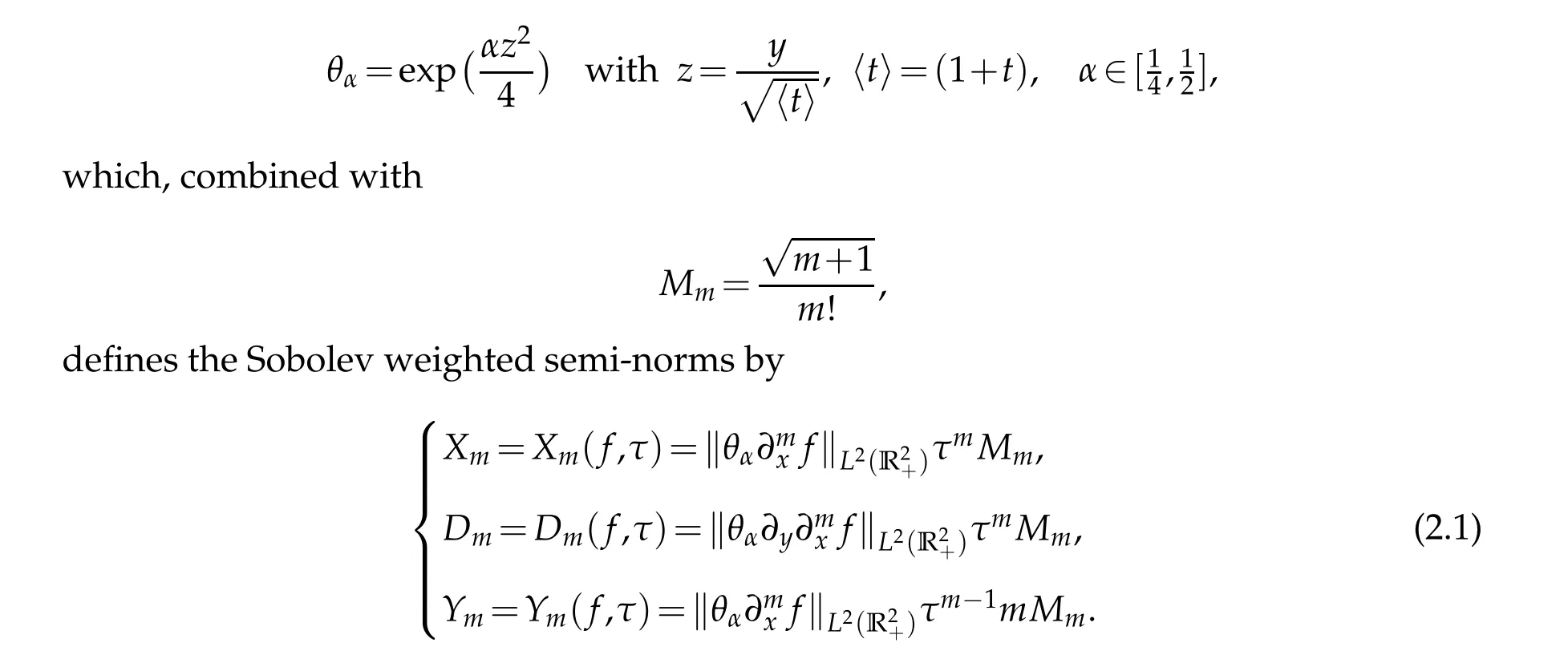
The above theorem is the main part of this paper,and its proof follows from the discussion in Sections 3 and 4.

Before proving the theorem,we first list some important inequalities as follows. The following main estimates on the functions in the norms defined in the previous section will be used frequently,whose proofs are given in[7,24,46].

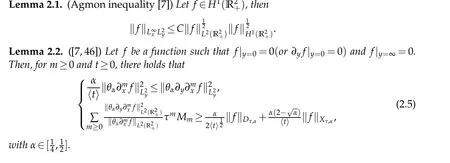
Proof.For the convenience of the readers,we will prove the second inequality as follows.Actually,by the first inequality,we have

3 Uniform estimates

In this section,we will prove the existence of solutions for the two dimensional Prandtl-Hartmann regime in the analytic framework defined in Section 2 by the standard energy method.

Now, we are ready to establish uniform estimates for the solutions to system (1.1)-(1.3).For our purpose,we first rewrite the solutions(u1,u2)to(1.1)-(1.3)as a perturbation(u,v)around the point(¯u,0)by standing for

We now deal with each term in(3.5) as follows. For the first term,the last term and the fourth term,we have,respectively

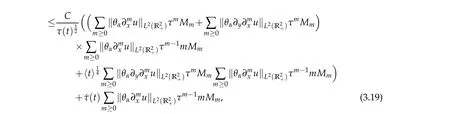
where we have used the fact that for any positive sequences{aj}j≥0and{bj}j≥0,

We have completed the proof of the existence of solutions to the 2D Prandtl-Hartmann equations(3.2)-(3.4)with damping term,and derived the lifespanTεof solutions.

4 Uniqueness

Next,we are going to prove the uniqueness of solutions to Eqs. (3.2)-(3.4). Letu1(t,x,y)andu2(t,x,y) are two solutions to the Eqs. (3.2)-(3.4) with same initial datau1(0,x,y)=u2(0,x,y)∈Xτ0,α. Represent the tangential radii of analytic regularity ofu1andu2byτ1(t)andτ2(t)respectively,which satisfy the bounds in Theorem 2.1.

Defineτ(t)to sovle

whereδ∈(0,1)is a small constant.This implies the uniqueness sinceu(0)=0.

The proof of uniqueness is thus complete. □

Combining(3.24)with(4.22),we complete the proof of Theorem 2.1. □

5 Concluding Remarks

In this paper, we prove the global existence and uniqueness of solutions to 2D Prandtl-Hartmann equations by using the classical energy methods in analytic framework. Besides,we got also the another two results for the classical Prandt equations and the mixed Prandtl equations in previous manuscripts[47,48]in Sobolev framework respectively.

In[47],we investigated the local existence of solutions to two-dimensional nonlinear Prandtl equations by energy methods in an exponential weighted Sobolev space. The main difficulty is the loss ofx-derivative by the termv∂yu,it is necessary to use a type of cancellation mechanism in the analysis. Thus,we constructed a new unknown function to avoid the loss ofxderivative.

In[48],we studied the local existence and uniqueness of solutions to two-dimensional mixed Prandtl-Shercliff equations by using the classical energy methods in Sobolev space. Compared to the existence and uniqueness of solutions to the classical Prandtl equations where the monotonicity condition of the tangential velocity plays a key role,which is not needed for the 2D Prandtl-Hartmann equations in analytic framework. Besides, the existence and uniqueness of solutions to the 2D MHD boundary layer where the initial tangential magnetic field has a lower bound plays an important role,which is not needed for the 2D Prandtl-Hartmann equations in analytic framework,either.

Acknowledgments

The authors are grateful to the editor and the reviewers for helpful comments and suggestions that greatly improved the presentation of a previous version of the manuscript.This paper was in part supported by the National Natural Science Foundation of China with contract number 12171082 and the fundamental research funds for the central universities with contract number 2232021G-13.