Asymptotic Behavior of Solutions for the Porous Media Equations with Nonlinear Norm-type Sources
2022-12-29XUEYingzhen
XUE Yingzhen
School of Business,Xi’an International University,Xi’an 710077,China.
Abstract. In the paper, the asymptotic behavior of the solution for the parabolic equation system of porous media coupled by three variables and with weighted nonlocal boundaries and nonlinear internal sources is studied. by constructing the upper and lower solutions with the ordinary differential equation as well as introducing the comparison theorem, the global existence and finite time blow-up of the solution of parabolic equations of porous media coupled by the power function and the logarithm function are obtained. The differential inequality technique is used to obtain the lower bounds on the blow up time of the above equations under Dirichlet and Neumann boundary conditions.
Key Words: Porous media equations; norm-type sources; the global existence; the finite time blow-up;the blow up time.
1 Introduction
In this article, we consider the following nonlocal cross-coupled porous medium equations
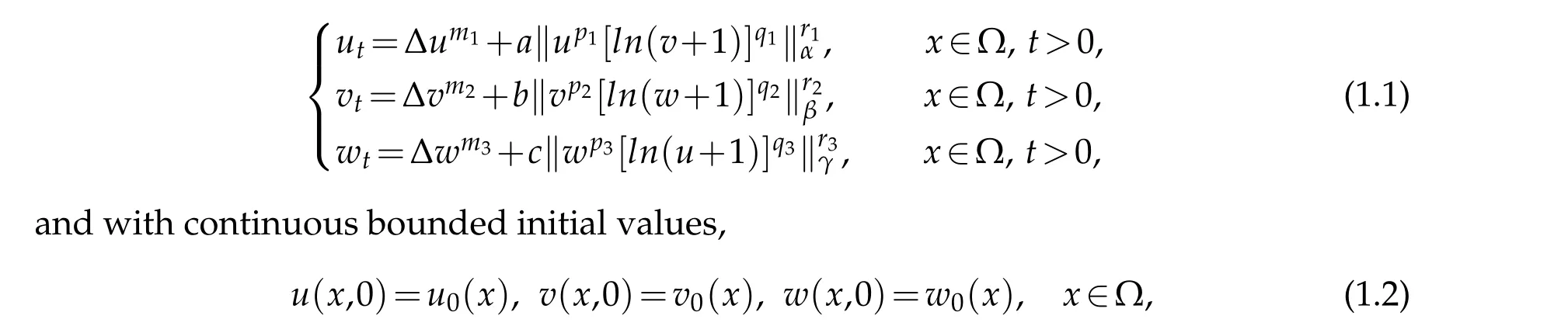
when the equations has weighted nonlocal boundary flow,

sufficient conditions for global existence and blow up of solutions in finite time are obtained. When the equations have Dirichlet boundary conditions,

under homogeneous Dirichlet boundary conditions, whenpq
Payn and Philippin in literature [6] have studied blow-up at a finite time and lower bound of blow up time of solution for the following parabolic equations
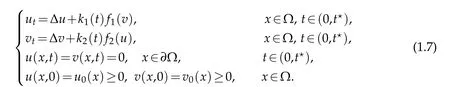
Tao and Fang in Literature[7] established blow-up at a finite time and lower bound of blow up time of solution for the following parabolic equations whenm1=1,m2=1,blow up at a finite time and lower bound of blow up time of solution.

Other results on the global existence, blow up and lower bound of blow up time of solutions for parabolic systems in porous media with nonlocal sources,see[8-18].
Inspired by the above literature, the logarithmic function is taken as the coupling variable of norm source for the first time, and the global existence,the finite time blow up and lower bound estimation of blow up time for nonlinear norm source porous media equations with cross coupling of power function and logarithmic function under different boundary conditions are studied in this paper.
2 Preliminary knowledge
It is well known that the system of parabolic equations of porous media do not necessarily have classical solutions.The following is the definition of the weak solutions of Eqs.(1.1)-(1.3).
Definition 2.1.Function u(x,t),v(x,t),w(x,t)∈Ω×[0,T]is termed as the upper (or lower)solutions of Eqs.(1.1)-(1.3). If the following conditions are true:
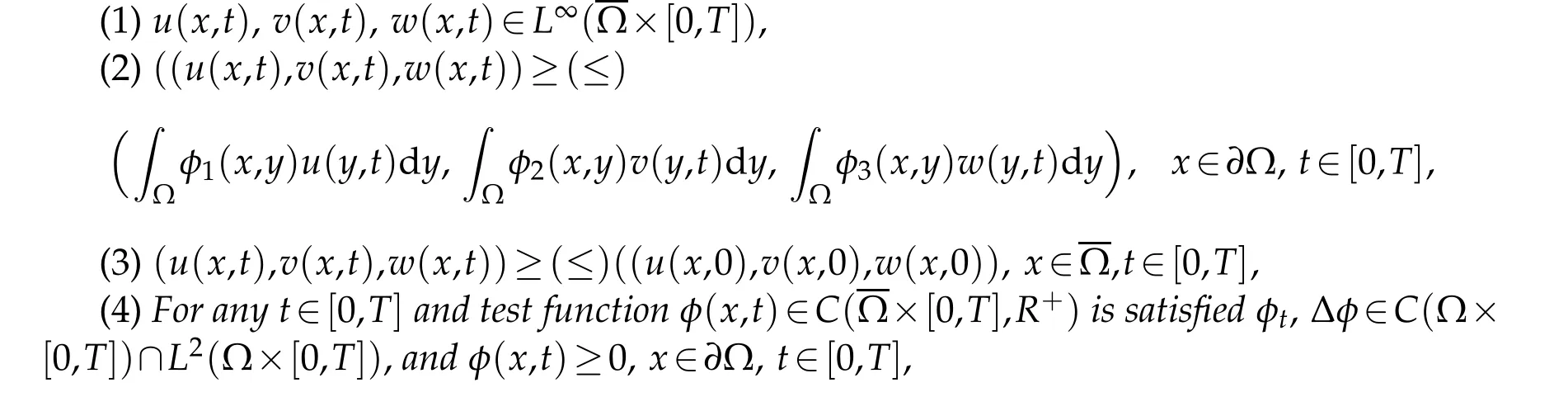

According to Literature[16],the comparison theorem is as follows:
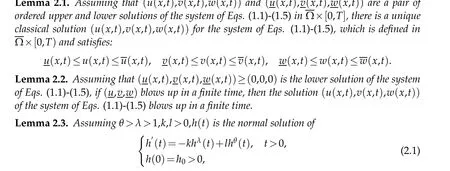
when h0is sufficiently large,h(t)>2blows up in a finite time.
Lemma 2.4.Assuming λ2>λ1>1,θ2>θ1>1,there exists such an h(t)like that in Lemma2.3that satisfies
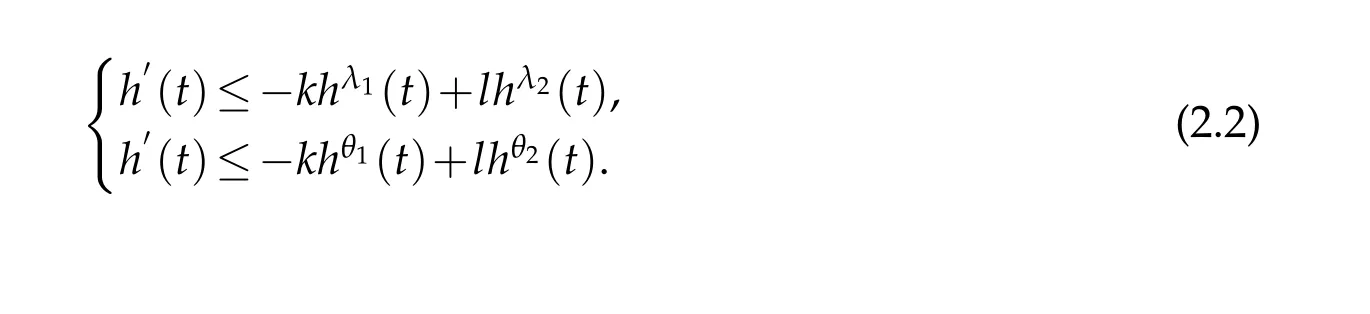
The proofs of Lemma 2.3 and Lemma 2.4 are shown in Literature[17].
Lemma 2.5.(Membrane inequality)
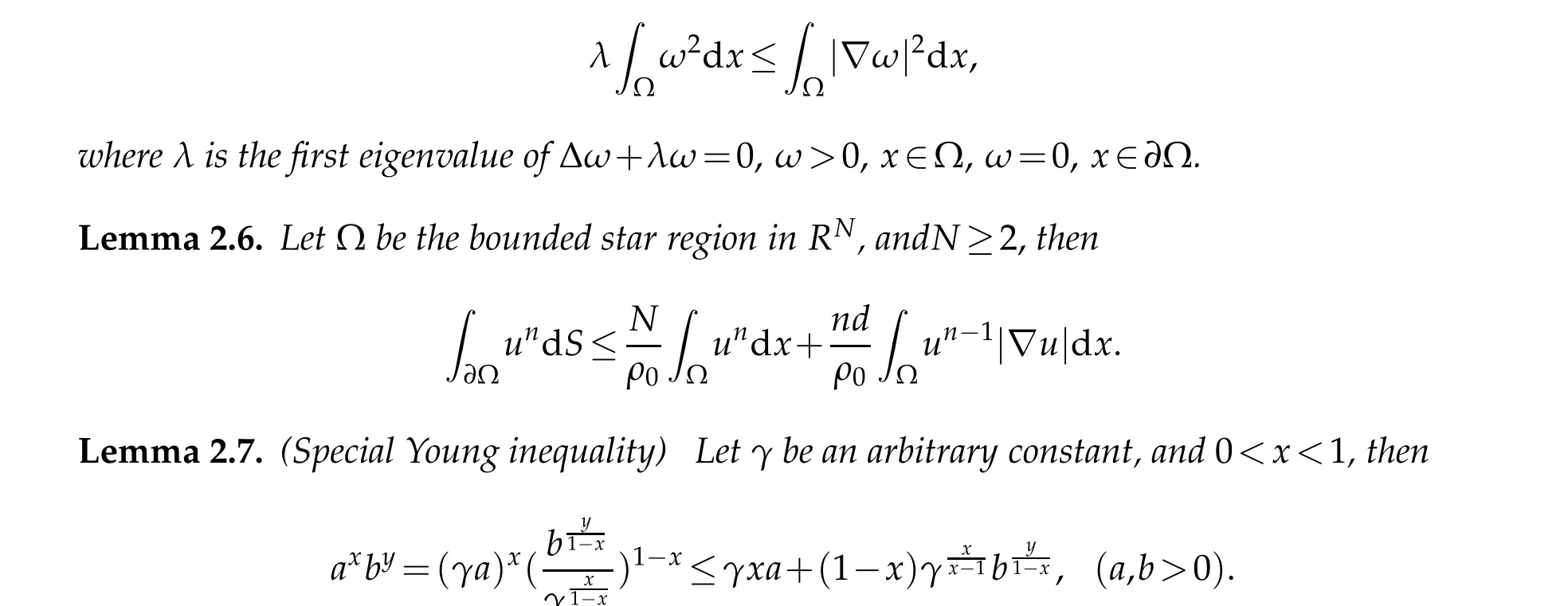
3 Global existence
Theorem 3.1.If one of the following conditions holds,the solution of the Eqs.(1.1)-(1.3)globally exists.




chooseKis sufficiently small,can be usedK≤min{C1,C2,C3},assumeu0(x),v0(x),w0(x)is sufficiently small, using the proof process of the first case in the similar Theorem 3.1,we can prove(u(x,t),v(x,t),w(x,t))s also the weak upper solution of the system of Eqs.(1.1)-(1.3),the solution of the Eqs.(1.1)-(1.3)globally exists.
(3)Ifm1>r1p1,m2>r2p2,m3>r3p3,(m1−r1p1)(m2−r2p2)(m3−r3p3)=r1r2r3q1q2q3,then,there are three constantsl1,l2,l3,make
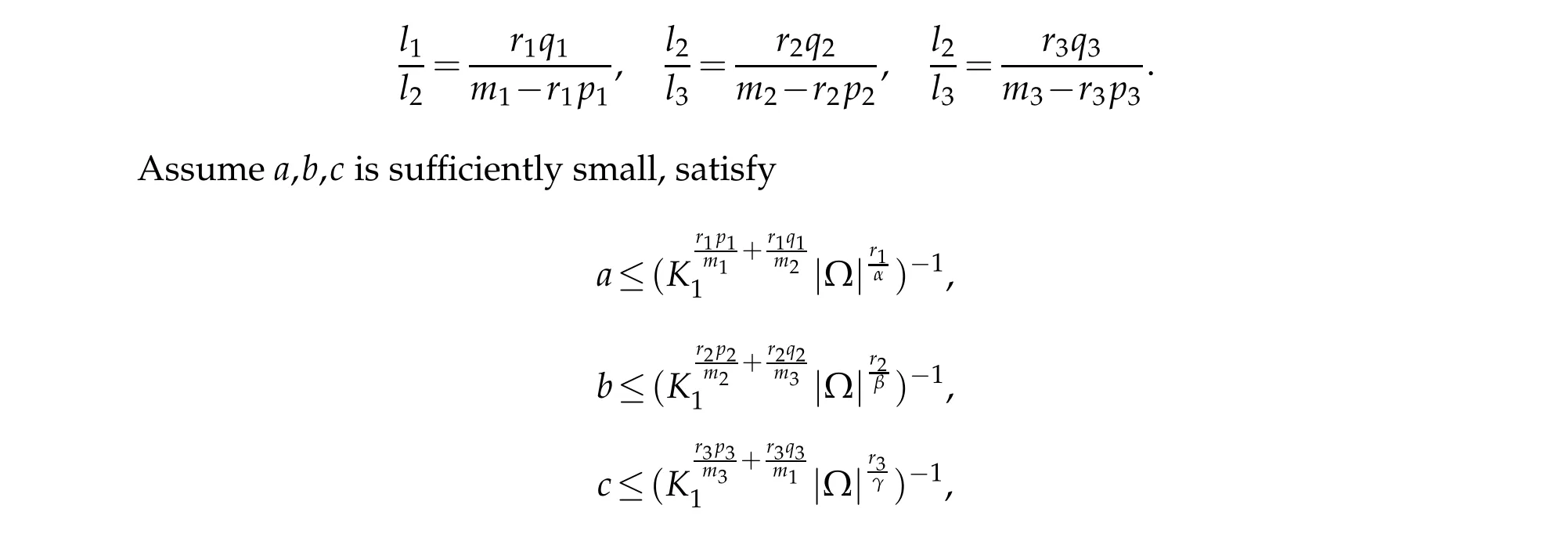
we know that Eqs. (3.13) and (3.14) permanently true. ChooseKis sufficiently large,it can also be proved (u(x,t),v(x,t),w(x,t))that is also the weak upper solution of the system of Eqs. (1.1)-(1.3),according to the comparison theorem,u(x,t)≤u(x,t),v(x,t)≤v(x,t),w(x,t)≤w(x,t),u(x,t),v(x,t),w(x,t)is the solution of Eqs.(1.1)-(1.3),the solution ofu(x,t),v(x,t),w(x,t)globally exists,the proof of Theorem 3.1 is completed.
4 Finite time blow-up of solutions
Theorem 4.1.If one of the following conditions holds,the solution of Eqs.(1.1)-(1.3)blow up in a finite.
(1)m1>r1p1,m2>r2p2,m3>r3p3,and(m1−r1p1)(m2−r2p2)(m3−r3p3) (2)m1 (3)m1>r1p1,m2>r2p2,m3>r3p3,(m1−r1p1)(m2−r2p2)(m3−r3p3)=r1r2r3q1q2q3,and u0(x),v0(x),w0(x)is sufficiently large. Therefore,(u,v,w)is the lower solution of Eqs.(1.1)−(1.3),and(u,v,w)blows up in a finite time. According to Lemma 2.2,the solution of Eqs.(1.1)−(1.3)blows up in a finite time. The following is to prove the existence ofl1,l2,l3that satisfy Eq. (4.7), there are three cases to discuss: (1) Ifm1>r1p1,m2>r2p2,m3>r3p3, (m1−r1p1)(m2−r2p2)(m3−r3p3) that is,Eq.(4.7)is true,Eq. (4.8)permanently true. (2)Ifm1≤r1p1orm2≤r2p2orm3≤r3p3, then,there are three constantsl1,l2,l3,using the proof process similar to the first case,we can prove that Eq. (4.8)permanently true. (3)Ifm1>r1p1,m2>r2p2,m3>r3p3, (m1−r1p1)(m2−r2p2)(m3−r3p3)=r1q1r2q2r3q3,then,there are three constantsl1,l2,l3keep thereby Takingθ=λ=max{m1l1−l1+1,m2l2−l2+1,m3l3−l3+1}, andθ=λ>1, based on Lemma 2.3,we obtain therefor,blow up in a finite time ofh(t),according to lemma 2.4,Eq.(4.7)is true,Eq.(4.8)permanently true.The proof of Theorem 4.1 is completed. The lower bound of blow up time for solutions of Eqs.(1.1)-(1.2)under Dirichlet boundary conditions(1.4)is discussed below. Theorem 5.1.Defines auxiliary functions First,the Lagrange’s mean value theorem and H¨older inequality is used to estimate the second term of Eq.(5.4),and it is obtained that The lower bound of blow up time for solutions of Eqs.(1.1)-(1.2)under Neumann boundary conditions(1.5)is discussed below. Theorem 6.1.Define the same measure as(5.1)and the same condition as k. If(u,v)is a nonnegative classical solution to the equation set(1.1)with(1.2)and(1.5), then the lower bound of t⋆is wherer1is an arbitrary constant. H¨older inequality is used to estimate the second term on the right side of Eq. (6.2),we have Eq.(6.7)becomes Integrating(6.8)from 0 tot⋆we obtain that is, the same measure relation is obtained with Eq. (5.3). Therefore, whenl≤0, the lower bound of blow up time of the equation set (1.1) with (1.2) and (1.5) is consistent with that of Eq.(5.26). Acknowledgments This work was supported by Natural Science Basic Research Project of Shaanxi Province(2019JM-534),Soft Science Project of Shaanxi Province(2019KRM169),Project of Qi Fang Education Research Institute of Xian International University (21mjy07), Special project support of the 14th five year plan of the China Association of Higher Education (Topic name:Research on the adaptability of specialty structure and industrial structure of Local Universities–a case study of Shaanxi Province,No:21DFD04),2021 youth innovation team construction scientific research plan project of Shaanxi Provincial Department of Education(21JP105), The Youth Innovation Team of Shaanxi Universities, Shaanxi educational science ”14th five year plan” project (SGH21Y0308). The author would like to deeply thank all the reviewers for their insightful and constructive comments.

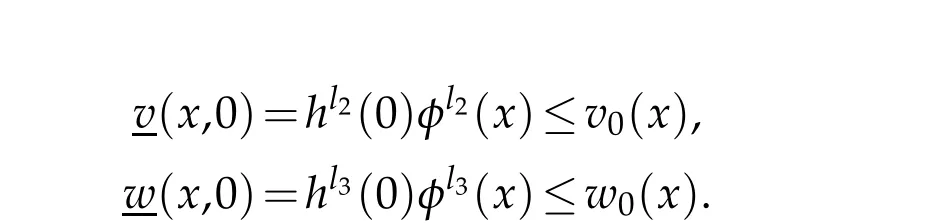

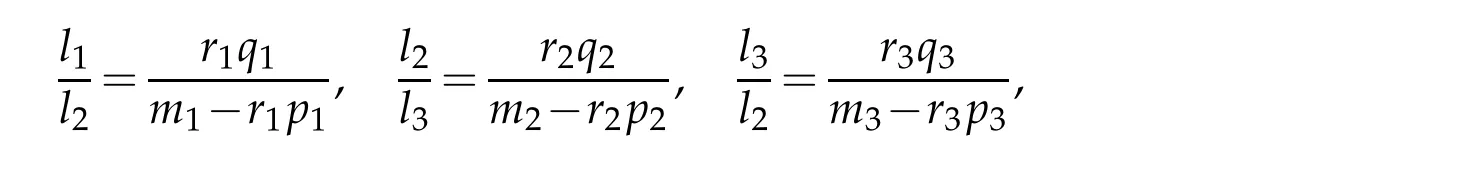
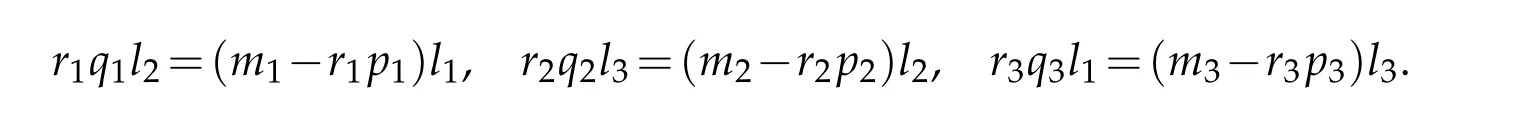
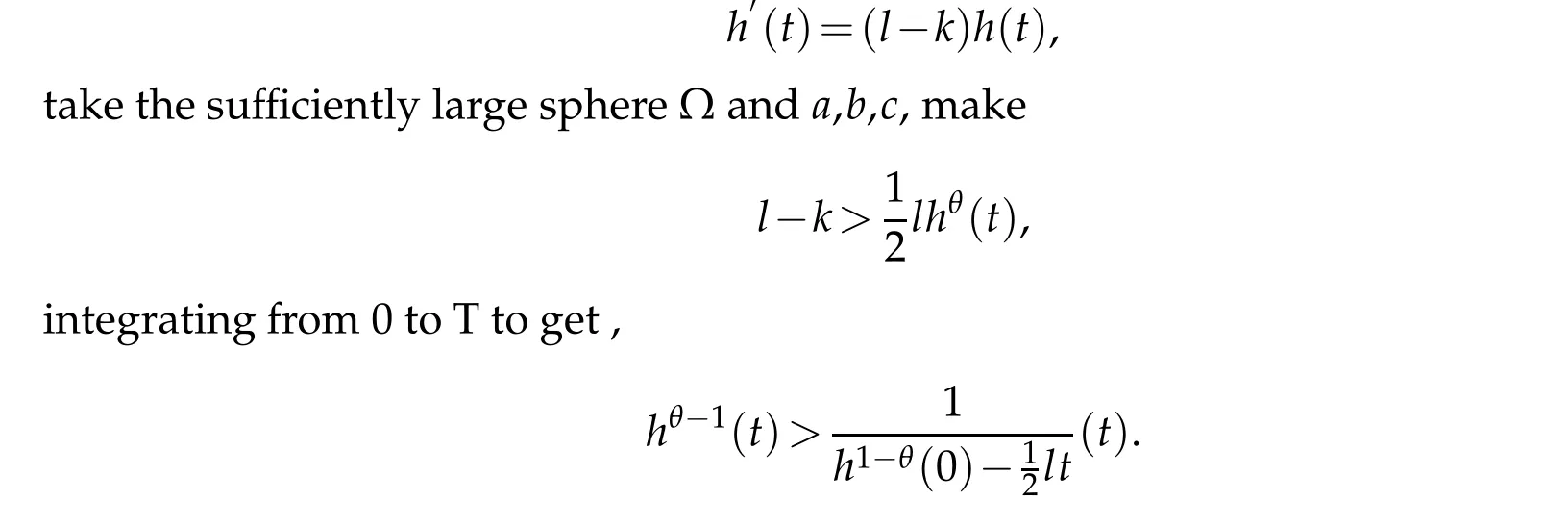
5 Lower bound of blow up time under Dirichlet boundary conditions






6 Lower bound of blow up time under Neumann boundary conditions
6.1 When l>0
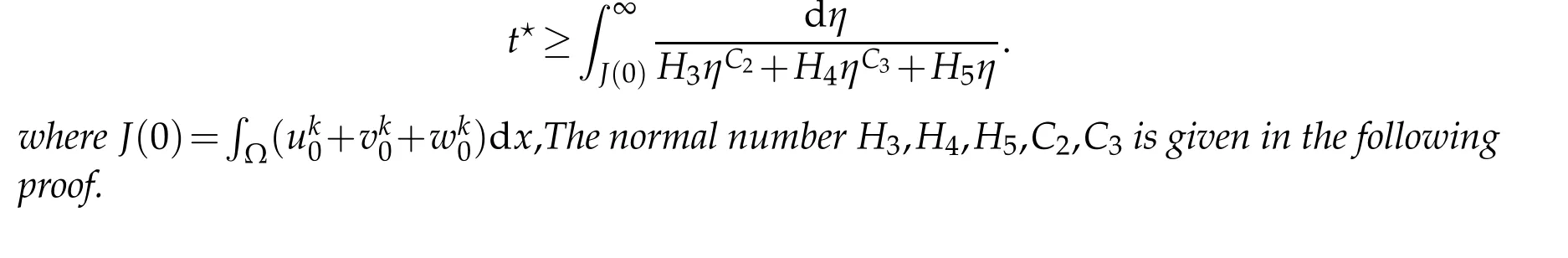


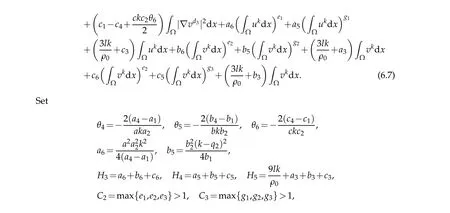
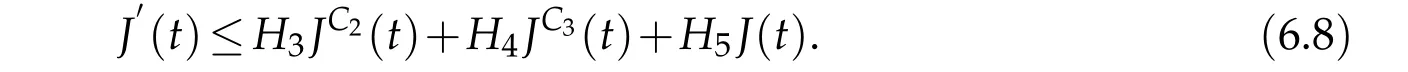
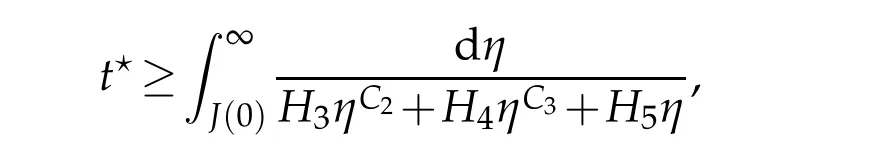
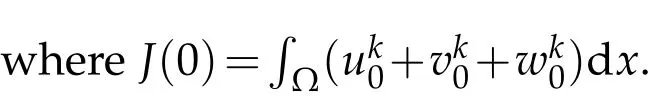
6.2 When l ≤0
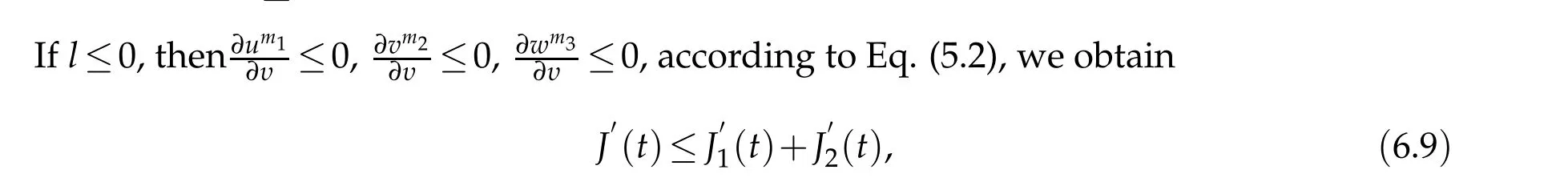
杂志排行
Journal of Partial Differential Equations的其它文章
- Mean Field Equations for the Equilibrium Turbulence and Toda Systems on Connected Finite Graphs
- A Weighted Singular Trudinger-Moser Inequality
- Stochastic Averaging Principle for Mixed Stochastic Differential Equations
- Infinitely Many Solutions for the Fractional Nonlinear Schr¨odinger Equations of a New Type
- Study of Stability Criteria of Numerical Solution of Ordinary and Partial Differential Equations Using Eulers and Finite Difference Scheme
- Global Well-Posedness of Solutions to 2D Prandtl-Hartmann Equations in Analytic Framework
