A Weighted Singular Trudinger-Moser Inequality

YU Pengxiu

School of Mathematics,Renmin University of China,Beijing 100872,China.

Abstract. In this paper, we obtained the extremal function for a weighted singular Trudinger-Moser inequality by blow-up analysis in the Euclidean space R2. This extends recent results of Hou(J.Inequal. Appl.,2018)and similar result was proved by Zhu(Sci. China Math.,2021).

Key Words: Singular Trudinger-Moser inequality;extremal function;blow-up analysis.

1 Introduction

where 4πis the best constant. The best means that whenα>4π,all integrals in(1.1)are finite, but the supremum is infinite. It is interesting to study whether the supremum in(1.1) can be attained or not. The first case for the attainability was proved by Carleson-Chang[1]when Ω is a ball in Rn(n≥2).Then Struwe[6]extend the above result when Ωis close to a ball in measure and Flucher[7]get the relevant results with arbitrary domains in R2. Later,Lin[8]derived a result with bounded domain in Rn(n≥2). This inequality(1.1)takes many forms. Chang-Yang[9]generalized(1.1)to the following form:

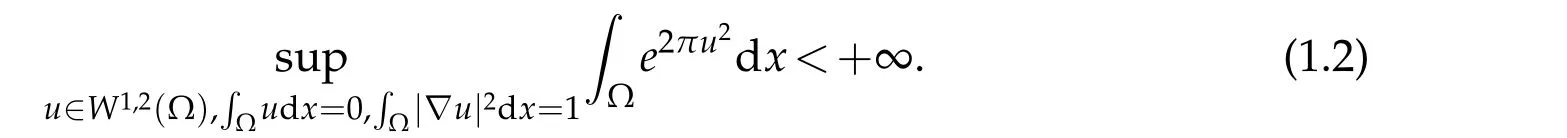
Recently,Hou[10]considers the classical Trudinger-Moser inequality(1.1)with weights,namely,for any 0≤α<λ1(Ω),

where 4π(1−β) is the best constant. On this topic, we refer the reader to Adimurthi-Yang[12],Csato-Roy[13],Iula-Mancini[14],Li-Yang[15],Yang-Zhu[16,17]. Particularly,Zhu[18]generalized(1.4)to the following conclusion:0∈∂Ω,for anyβ∈(0,1),there have

where 2π(1−β)is the best constant.There are many applications of(1.1)not only in Euclidean space,but also in Riemannian manifold,see for example,Ding-Jost-Li-Wang[19],Li[20,21],Li-Liu[22],Yang[23,24],Yang-Zhou[25],Yang-Zhu[26]Zhu[27]and Yu[28].

In this paper,motivated by(1.3)and(1.5),we consider a weighted singular Trudinger-Moser inequality. Our conclusion reads as follows.

Theorem 1.1.LetΩ⊂R2be a smooth bounded domain with0∈∂Ω. For any β∈(0,1),g∈C0(Ω)with g≥0and g(0)>0,there holds

In order to prove Theorem 1.1,we follow the lines of[18]and mainly use the method of blow-up analysis. As a comparison with results of Zhu[18],we should mention that,there are more detailed analysis to do. Particularly,we use more coordinate transformations in our situation.

The remaining part of this article is organized as follows: In Section 2, we prove 2π(1−β) is the best possible constant by constructing test functions; In Section 3, we get an upper bound of (1.6) by blow-up analysis; In Section 4, we construct a sequence of functions to complete the proof of Theorem 1.1. Throughout this paper, we do not distinguish sequence and subsequence. Moreover,we often denote various constants by the sameC.

2 2π(1−β)is the best possible constant.

Hence, with (2.6) and (2.7), we conclude that 2π(1−β) is the best possible constant in(1.6).

3 Blow-up analysis

In this section,we prove the inequality(1.6)holds by means of blow-up analysis. Firstly,the existence of maximizers for subcritical functionals is proved and the corresponding Euler-Lagrange equation is given. Secondly,the asymptotic behaviour of maximizer and the convergence behaviour of points away from maximizer are researched separately.Finally,we use the capacity method to obtain an upper bound of the inequality(1.6)for the occurrence of blow-up. Our proof consists of the following lemmas.

For the proof of lemma 3.1 is totally similar to[18,lemma 2.1],so it is omitted.what’s more,it is easy to calculate thatuεsatisfies the following Euler-Lagrange equation,namely

From lemma 3.6,we have the following corollary.

Corollary 3.6.1.For any θ∈(0,2),there holds

4 Existence of extremal functions.

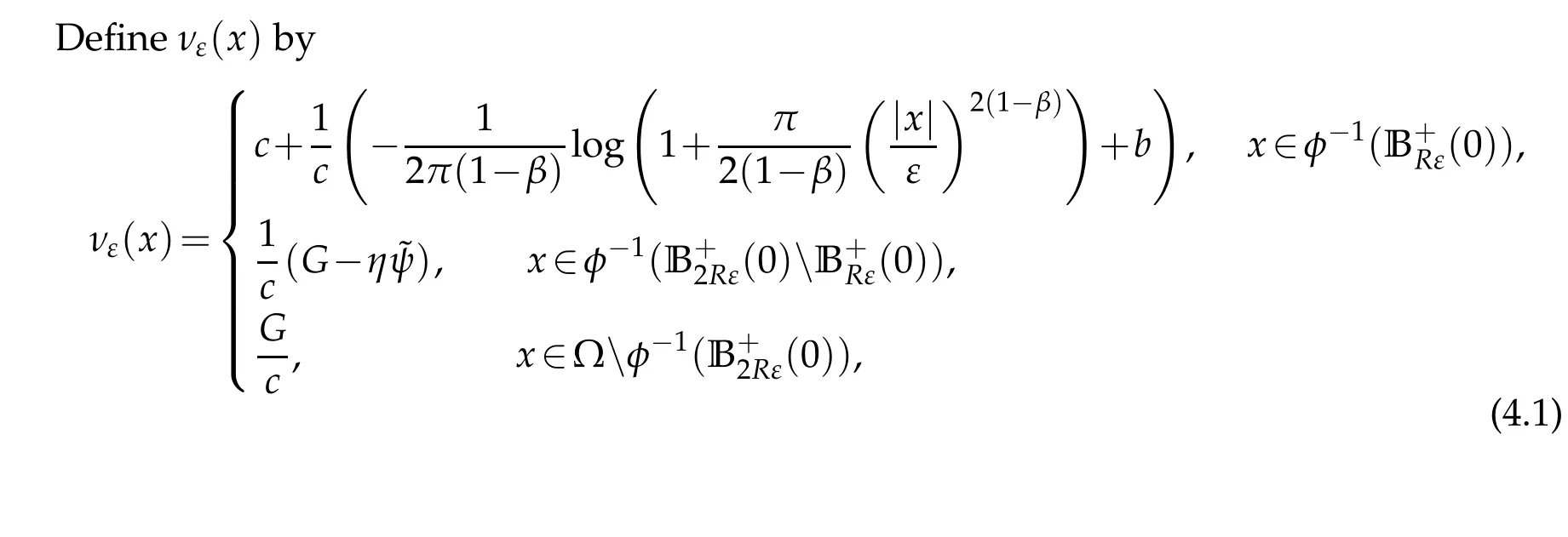
for sufficiently smallε>0. However(4.7)contradicts(3.29). Therefore,we obtain Theorem 1.1.