Mean Field Equations for the Equilibrium Turbulence and Toda Systems on Connected Finite Graphs

ZHU Xiaobao

School of Mathematics,Renmin University of China,Beijing 100872,China.

Abstract. In this paper,we study existence of solutions of mean field equations for the equilibrium turbulence and Toda systems on connected finite graphs. Our method is based on calculus of variations, which was built on connected finite graphs by Grigor’yan,Lin and Yang.

Key Words: Mean field equation;equilibrium turbulence;Toda system;finite graph.

1 Introduction

LetG=(V,E)be a connected finite graph,whereVis the vertex set andEthe edge set.For every edgexy∈E,we assume its weightwxy>0 andwxy=wyx.Denote byµa positive and finite measure onV. Let us review some definitions first.

Definition 1.1.For any function f on V,theµ-Laplacian of f is defined by

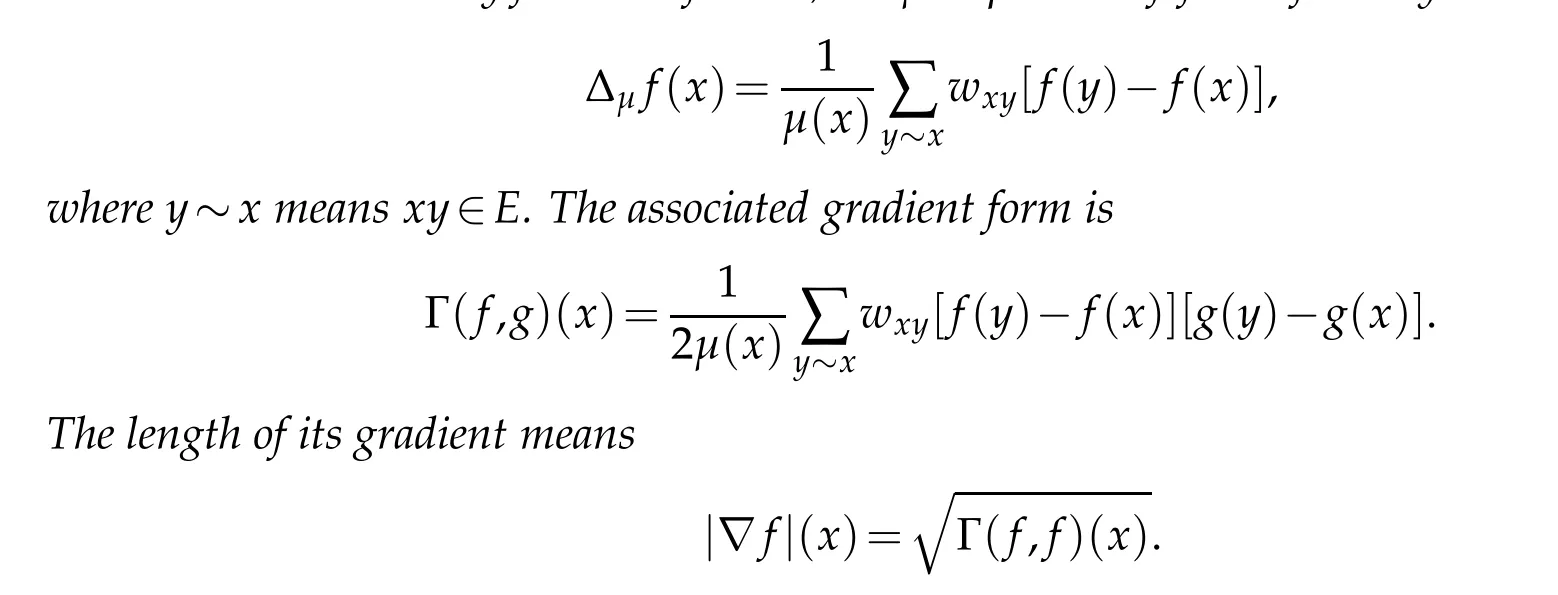
has a solution on V.

On a compact Riemann surface(Σ,g),Eq. (1.1)describes the mean field of the equilibrium turbulence with arbitrarily signed vortices[1–3]and was obtained in[4,5]from different statistical arguments. Whenψ=1/|Σ|, Ohtsuka and Suzuki [6], using a variational argument, proved that Eq. (1.1) can be solved if 0 ≤c1,c2<8πandh1=h2=1;Zhou [7,8] gave a sufficient condition for the existence of solutions of Eq. (1.1) whenc1=c2=8πandh1=h2=1;moreover,she studied the supercritical case of the existence of solutions of(1.1). These results partially generalized the existence results about Kazdan-Warner problem in[9].

On a compact Riemann surface (Σ,g), Eq. (1.2) is related to non-Abelian Chern-Simons model [10]. Whenψ=1/|Σ|, Jost-Wang [11] proved the Moser-Trudinger inequality for Toda system.Based on this inequality,Li-Li[12]and Jost-Lin-Wang[13]gave a sufficient condition for the existence of solutions of the Toda system withλ1=λ2=4π,which is the critical case in the sense of the Moser-Trudinger inequality.For more relevant study,we refer the interesting reader to the references therein.

Recently, in a series of papers, Grigor’yan-Lin-Yang [14–16] founded the variational method for semi-linear elliptic equations on connected finite graphs and locally finite graphs. Based on this method,many mathematicians studied equations with variational structure on graphs,see for example[17–25]and the references therein.

In this paper, motivated by [14], we are interested in the existence of solutions of mean field equations for the equilibrium turbulence and Toda systems on connected finite graphs. We shall pursue the variational method. We remark that, the existence of solutions of Eq.(1.1)on connected finite graphs and on compact Riemann surfaces are different.In connected finite graph case,Eq.(1.1)always has minimum solution ifc1,c2>0,however, in compact Riemann surface case, Eq. (1.1) does not have minimum solution ifc1orc2is bigger than 8π. Similarly, in connected finite graph case, Toda system(1.2)always has a minimum solution ifλ1,λ2>0,but in compact Riemann surface case,Toda system(1.2)does not have minimum solution whenλ1orλ2is bigger than 4π.

The rest of this paper is organized as follows: In Section 2, we present some well known knowledge about connected finite graphs. Then we prove our Theorems 1.1 and 1.2 in Sections 3 and 4 respectively. Throughout this paper, we useCto denote absolute constants without distinguishing them even in the same line;we do not distinguish sequence and its subsequence.

2 Preliminaries

In this section, we shall present some well known knowledge which are needed in the proofs of our main results, they come from [14] directly. Still, we shall give some short proofs for the convenience of readers.

LetG=(V,E)be a connected finite graph. Supposeu:V→R is a function,we define a norm

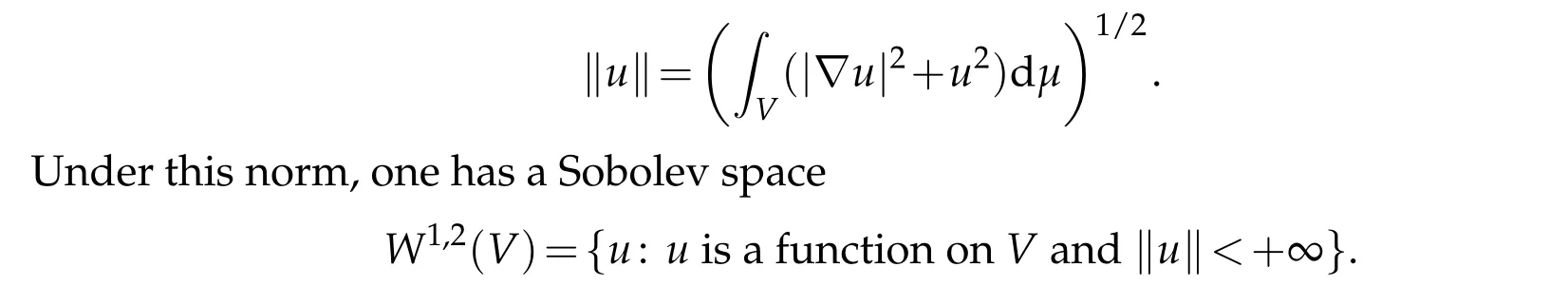
Since|V|is finite,we haveW1,2(V)=R|V|. ThenW1,2(V)is pre-compact,that is,

Lemma 2.1.If{uj}is bounded in W1,2(V),then there exists some u0∈W1,2(V)such that up to a subsequence,uj→u0in W1,2(V)as j→∞.

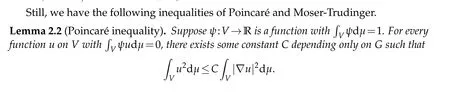
3 Proof of Theorem 1.1

4 Proof of Theorem 1.2

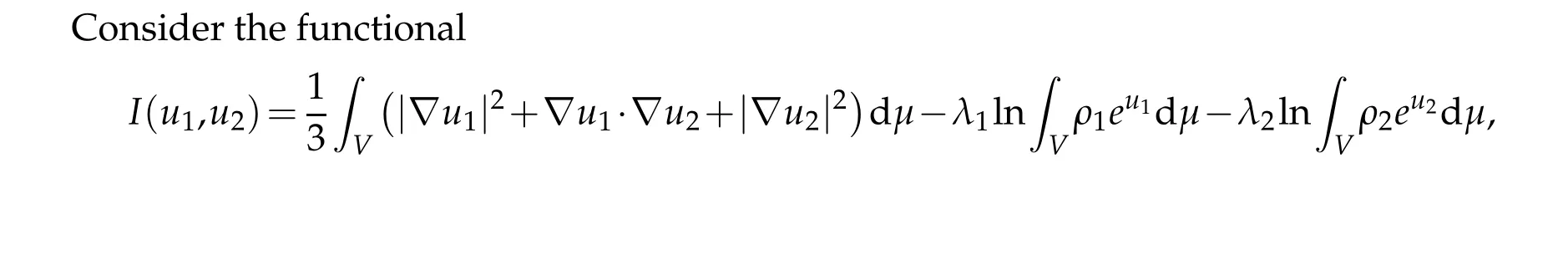
Acknowledgement

The main part of this work was finished when the author visited School of Mathematical Science, University of Science and Technology of China. He would like to thank Professor Jiayu Li for invitation and encouragement,thank Professor Yunyan Yang and Professor Shiping Liu for many helpful discussions. This work is partially supported by the National Science Foundation of China(Grant No.11401575 and 11721101).