Infinitely Many Solutions for the Fractional Nonlinear Schr¨odinger Equations of a New Type
2022-12-29GUOQingandDUANLixiu
GUO Qingand DUAN Lixiu
College of Science,Minzu University of China,Beijing 100081,China.
Abstract. This paper, we study the multiplicity of solutions for the fractional Schr¨odinger equation
Key Words: Fractional Schr¨odinger equations;infinitely many solutions;reduction method.
1 Introduction
In this paper,we consider the following nonlinear fractional Schr¨odinger equation whereP.V.is the principal value andc(N,s)=π2s+N2Γ(s+N2)/Γ(−s). For more details on the fractional Laplace operator,we can refer to[1,2].
The fractional Laplace operator appears in many fields such as biological modeling,physics and mathematical finance,and can be regarded as an infinitesimal generator of a stable L´evy process [3]. The fractional Laplace problem has recently been extensively studied, such as [4–22] Brezis-Nirenberg problems on lower dimensions, local uniqueness and periodicity for the prescribed scalar curvature problem, solutions of critical exponent via Local Pohozaev identities and the references therein.
Whens=1,the classical nonlinear Schr¨odinger equation

was derived from the Bose-Einstein condensates (BEC) originated in 1924-1925, when Einstein predicted that, below a critical temperature, part of the bosons would occupy the same quantum state to form a condensate ([23–25]). New experimental advances make many mathematicians study again the following of Gross-Pitaevskii(GP)equations proposed by Gross[26]and Pitaevskii[27]in the 1960s:


We construct a certain type of infinite many non-radial solutions of (1.1), and our main results are as follows:
Theorem 1.1.Suppose that N≥3,0 Theorem 1.1 can be shown by the following result. Theorem 1.2.Under the assumption of the Theorem1.1,there exists an integer k0,which satisfies for all integer k≥k0,then the above equation has the solution uk of the following form: In[16],Long,Peng and Yang considered equation(−∆)su+u=K(x)up,u>0, in RN.Under some asymptotic assumptions onK(x), they constructed infinitely many non-radial positive solutions,which concentrating at infinite vertices of a polygonal with infinitely large length of sides. Our method can also be applied to the problem(−∆)su+u=K(x)up,u>0,in RN, obtaining another type of solutions concentrating at infinite vertices of two similar equilateral polygonal with infinitely large length of sides. In this case,besides the length of each polygonal,we have to simultaneously handle one more parameterh, that is the height of the podetium. Another difficulty lies in the non-local property of the operator (−∆)sand the algebraic decay involving the approximation solutions make the estimates of the error terms become more subtle,in striking contrast to the classical Schr¨odinger problem in [28], where the approximation solution possess very fine exponential decay at infinity. This paper is organized as follows.In Section 2,we carry out the reduction procedure to obtain a finite dimensional setting. In Section 3, we solve the corresponding finite dimensional problem and prove the main result Theorem 1.1. Some technique estimates are put in the appendix. The following lemma proves that linear operator L is bounded and invertible from E to E. Lemma 2.2.There exists a constant ρ>0that is independent of the integer k,such that for any(r,h)∈Dk,Proof.We prove the lemma by contradiction. Suppose that whenk→∞, there exist(rk,hk)∈Dkandvk∈E satisfying Thus we can obtainAis a contracting mapping. Appendix A Energy expansion Acknowledgement The research of Q.Guo was supported by NNSF of China(No.11771469).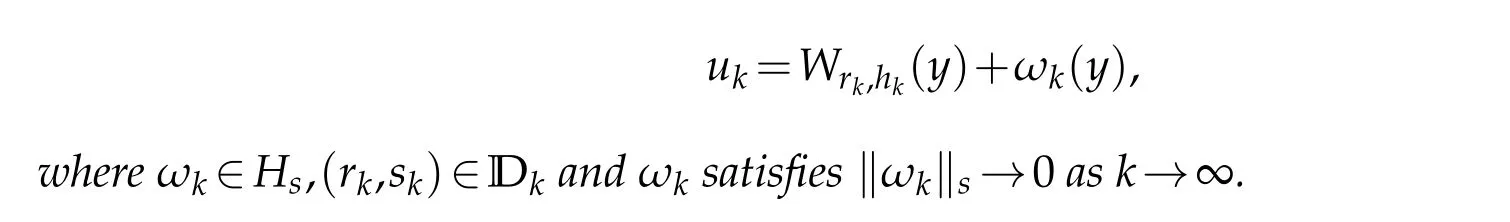
2 Preliminaries and the reduction framework
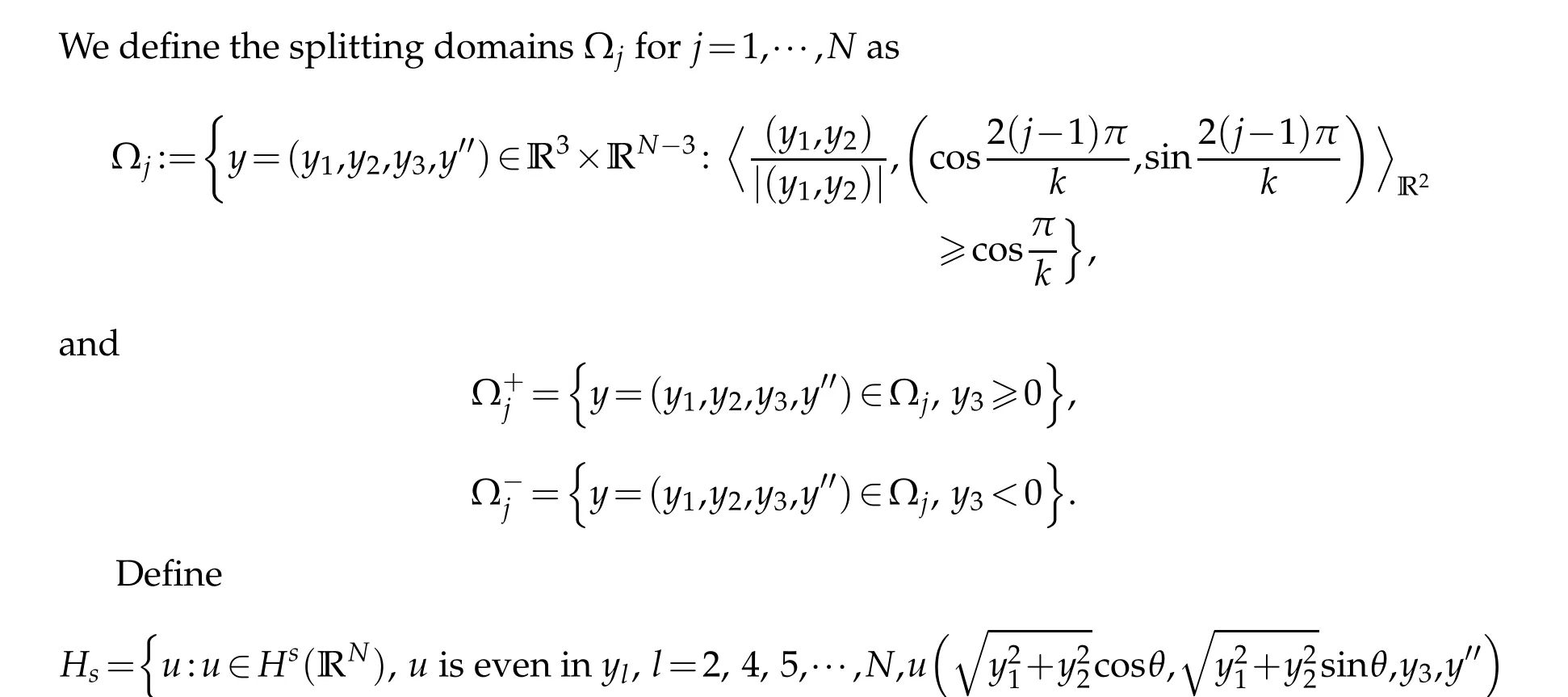


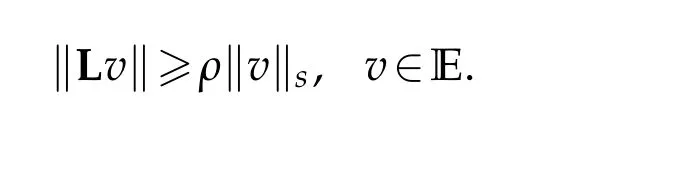





3 Finite dimensional problem


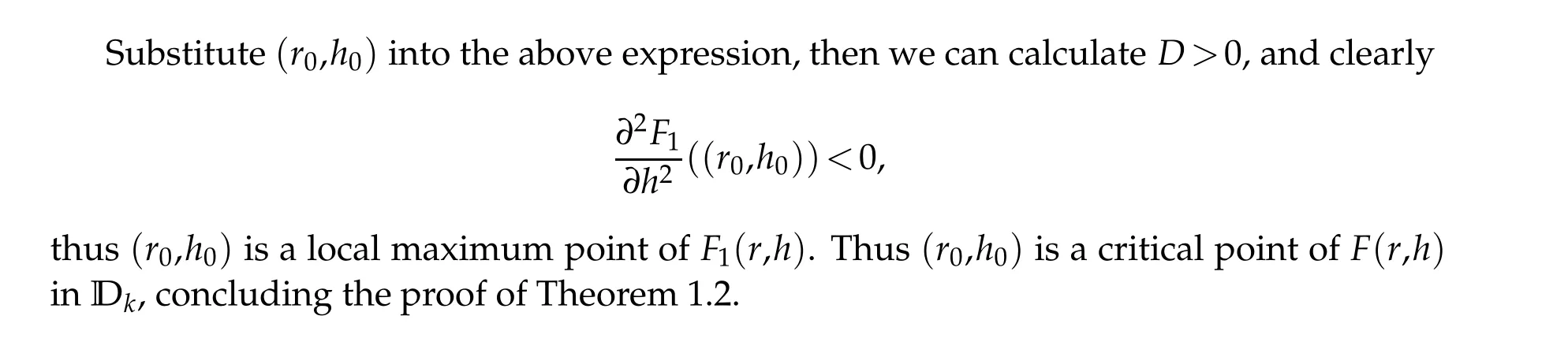






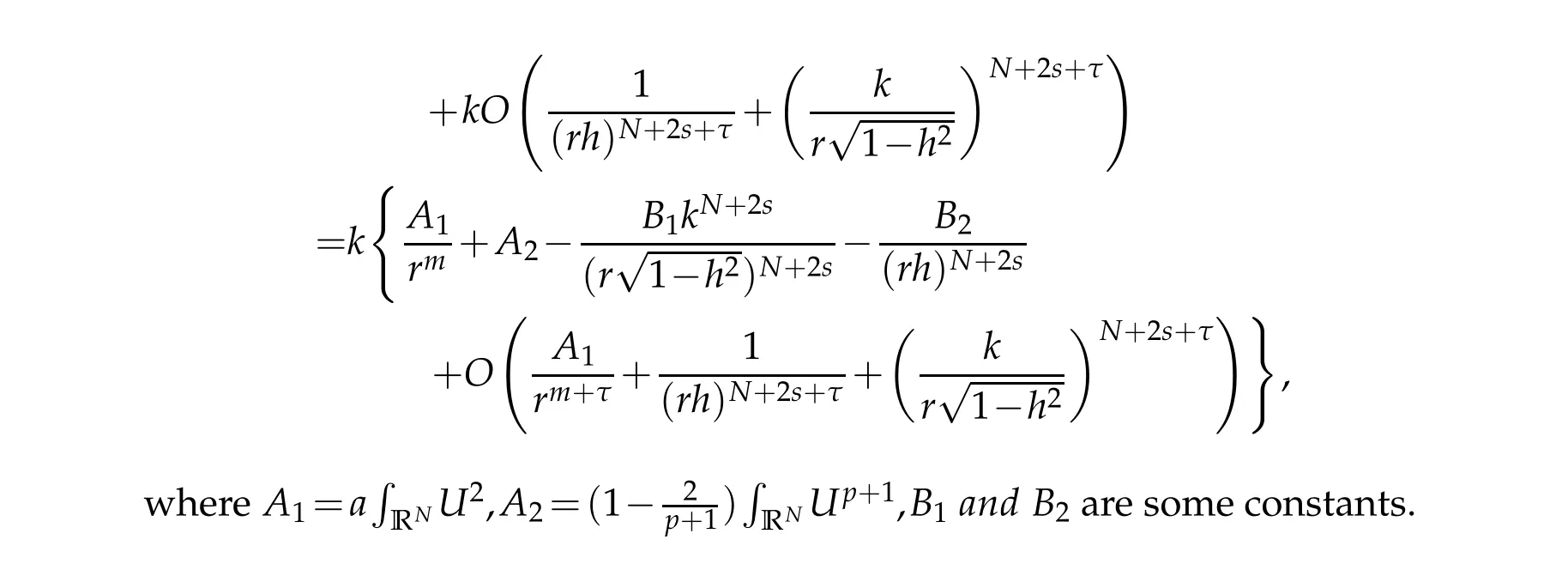
杂志排行
Journal of Partial Differential Equations的其它文章
- Mean Field Equations for the Equilibrium Turbulence and Toda Systems on Connected Finite Graphs
- A Weighted Singular Trudinger-Moser Inequality
- Stochastic Averaging Principle for Mixed Stochastic Differential Equations
- Asymptotic Behavior of Solutions for the Porous Media Equations with Nonlinear Norm-type Sources
- Study of Stability Criteria of Numerical Solution of Ordinary and Partial Differential Equations Using Eulers and Finite Difference Scheme
- Global Well-Posedness of Solutions to 2D Prandtl-Hartmann Equations in Analytic Framework
