Stochastic Averaging Principle for Mixed Stochastic Differential Equations
2022-12-29JINGYuanyuanPENGYarongandLIZhi
JING Yuanyuan,PENG Yarong and LI Zhi
School of Information and Mathematics,Yangtze University,Jingzhou 434023,China.
Abstract. In this paper, an averaging principle for the solutions to mixed stochastic differential equation involving standard Brownian motion,a fractional Brownian motion BH with the Hurst parameter H> 12 and a discontinuous drift was estimated.Under some proper assumptions, we proved that the solutions of the simplified systems can be approximated to that of the original systems in the sense of mean square by the method of the pathwise approach and the Itˆo stochastic calculus.
Key Words:Averaging principle;mixed stochastic differential equation;discontinuous drift;fractional Brownian motion.
1 Introduction
In this paper,we consider the following mixed stochastic differential equation:

whereX0∈R,t∈[0,T],a,b,c:[0,T]×R →R, andBHis a fractional Brownian motion with the Hurst parameterH∈(12,1). The processesWandBHcan be dependent. The integral w.r.t.Wiener processWis a standard Itˆo integral,and the integral w.r.t.BHis the pathwise generalized Lebesgue-Stieltjes integral which is defined in[1,2,3].
The strongest motivation to study such equations comes, in particular, from financial modeling. It is well known that there are two kinds of sources that affect prices in financial markets. The random noise from the first source usually prevails in a shorter time periods and can be modeled by a Wiener processW. While the random noise of the second source is coming from economical background and usually has a long range dependence property,which can be modeled by a H¨older continuous process with exponent greater thanγ>12, just like fractional Brownian motion. Consequently, the mixed model describes the stock price behavior in a better way. Moreover, one can note that the long-range influence in the financial markets and application of the models involving fractional Brownian motion and Brownian motion were established in many papers(see[4,5,6,7,8]and references therein).
Recently,the mixed stochastic differential equations(1.1) have attracted a great deal of attention.For example,Guerra and Nualart and Kubilius considered the existence and uniqueness for the strong solution to Eq.(1.1)in[3]and[9];Mishura and Shevchenko[10]studied the the existence,uniqueness and convergence of the solution to Eq.(1.1);and in[11],Mishura et al. investigated the the convergence of Euler approximations for mixed delay stochastic differential equations;while Liu and Luo discussed the mean square rate of convergence by using a modified Euler method in[12]; Melnikov et al. [13] obtained the stochastic viability and comparison theorems to Eq. (1.1). We notice that the shift coefficientsain the above papers are continuous inX. But,in many practical applications,the continuity of the shift coefficients is too strong to be satisfied. The first motivation of our work is to obtain the existence of strong solution to Eq. (1.1) whenacan be discontinuous inX.
Stochastic averaging principle,which enables to study the complex equations in terms of the related averaged one, plays an important role in multiscale problem (see, e.g.[14,15,16,17,18,19] and references therein). A stochastic averaging technique for SDEs only driven by fBm with Hurst parameterH∈(12,1)was developed by Xu et al. [20,21],and they proved that the original system can be approximated by the averaged systems in the method of mean square convergence and of convergence in probability;Li and Yan[22]estabilished the stochastic averaging for two-time-scale stochastic partial differential equations driven by fractional Brownian motion with Hurst parameterH∈(0,12). After that,Pei et al.[23]studied the averaging principle for multidimensional,time dependent,Eq. (1.1) with the situation that the drift term is continuous by combining the pathwise approach with the Itˆo stochastic calculus. Motivated by this work,the second motivation of our work is to consider a following interesting question: whenγ>12in Eq. (1.1), can the stochastic averaging principle establish if the coefficientais discontinuous? More precisely,we will establish the stochastic averaging principle for the strong solution of Eq. (1.1)whena(t,x)has linear growth and is left-continuous and lower semi-continuous inx.
The rest of this paper proceeds as follows. Section 2 presents preliminary results that are needed in the subsequent section. In Section 3, the existence of the strong solution to Eq. (1.1) will be established. A stochastic averaging principle for SDEs driven by standard Bm and fractional Brownian motion with the Hurst parameterH>12will be given in Section 4.
Throughout this paper,the letterKorCwith or without indexes will refer to positive constants whose values may change in different occasions.
2 Preliminaries
In this section,we present some definitions and assumptions which will be used later.
Let(Ω,F,F,P) be a complete probability space equipped with a filtration satisfying standard assumptions, and {W(t),t∈[0,T]} be a standard F-Wiener process. Let also{BH,t∈[0,T]} be an F-adapted stochastic process,i.e. a centered Gaussian process with covariance E[BHt BHs]=12(s2H+t2H−|t−s|2H).
2.1 Some notations
We consider two continuousf,g∈C([0,T];R+),following the work of Z¨ahle[1]and Samko et al.[24],forα∈(0,1)and 0≤a In order to attain the solution of Eq. (1.1),let us make some hypotheses. (ii) Linear growth:|a(t,x)|≤C(1+|x|). (H3) There exists a constantK5and for anyt∈[0,T],x,y∈R such that the following properties hold: (i) Lipschitz continuity inx: |a(t,x)−a(t,y)|≤K5|x−y|; (ii) Linear growth:|a(t,x)|≤C(1+|x|). (H4) There exists a constantK6and for anyt∈[0,T],x∈R such that To treat the existence of the solution to Eq. (1.1) of this section, firstly, we need the following approximation lemma and the reader is referred to[26]for the proof. Lemma 3.1.Supposing that a(t,x)satisfies the assumption(H2),then the sequence of functions is well defined for n≥L and it satisfies where the constantC(1),C(2)anddNis independent ofρ,f,hand depends onT, and constants from(H3). In this section, we are going to prove the stochastic averaging principle of solutions to the mixed stochastic differential equations under some appropriate assumptions.Fixε0,for eachε∈(0,ε0],we consider the following standard form of Eq.(1.1): where ¯a, ¯b, ¯c: R →R fulfill the same condition as witha,b,cin Eq. (4.1), this equation also exists a solutionYε(t). Besides,in order to obtain our results,similar to Lemma 3.1,we will use the following lemma. Lemma 4.1.Supposing that¯a(x)satisfies the assumption(H2),then the sequence of functions whereψi(T1)are positive bounded functions with limT1→∞ψi(T1)=0,i=1,2,3. Lemma 4.2.Suppose that Eq.(4.2)satisfies the conditions (H1), (H2) and (H4). Then, there exists a random variable CR>0,depending on BH,such that, Now,we claim and prove the main result in this paper. It shows that the solution of the averaged Eq.(4.2)converges to that of the original Eq.(4.1)in mean square sense. Theorem 4.1.Assuming that the original Eq.(4.1)and the averaged Eq.(4.2)both satisfy the Hypothesis (H1)-(H2) and(H4)-(H5). For a given arbitrarily small number δ1>0, there exists L>0,θ∈(0,1)and ε1∈(0,ε0]such that for all ε∈(0,ε1],we have holds,the proof is complete. Acknowledgement The authors thank the editors and the reviewers for their useful comments.

2.2 Assumptions



3 Existence of Solution






4 Stochastic Averaging Principle

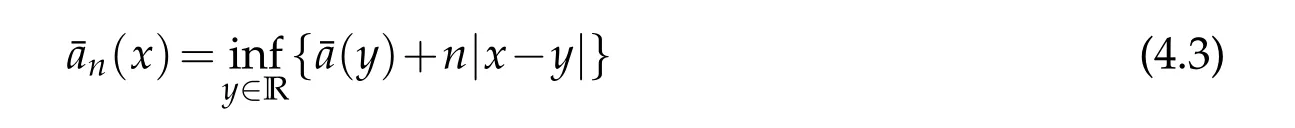
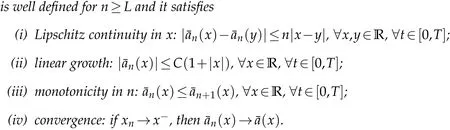


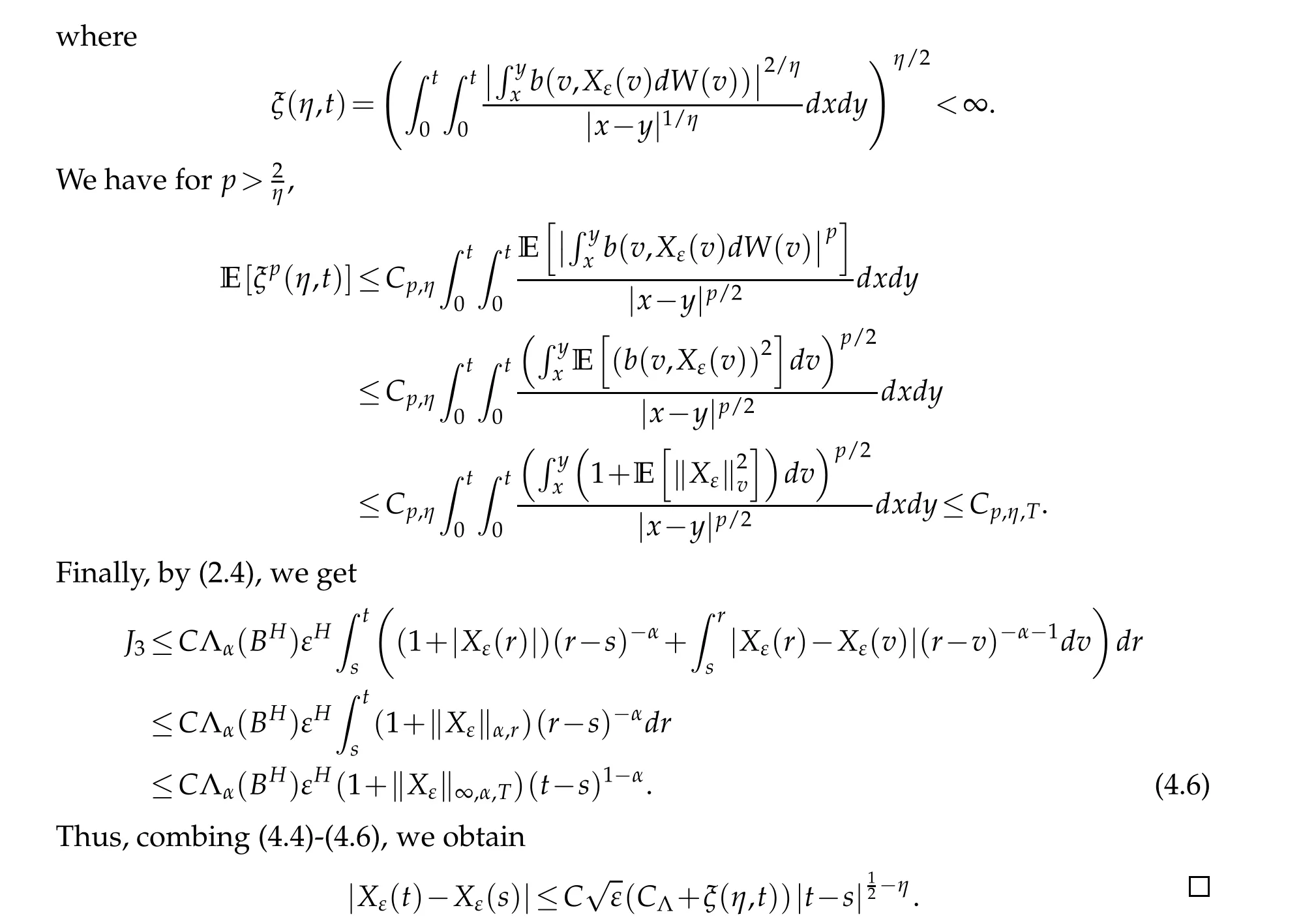
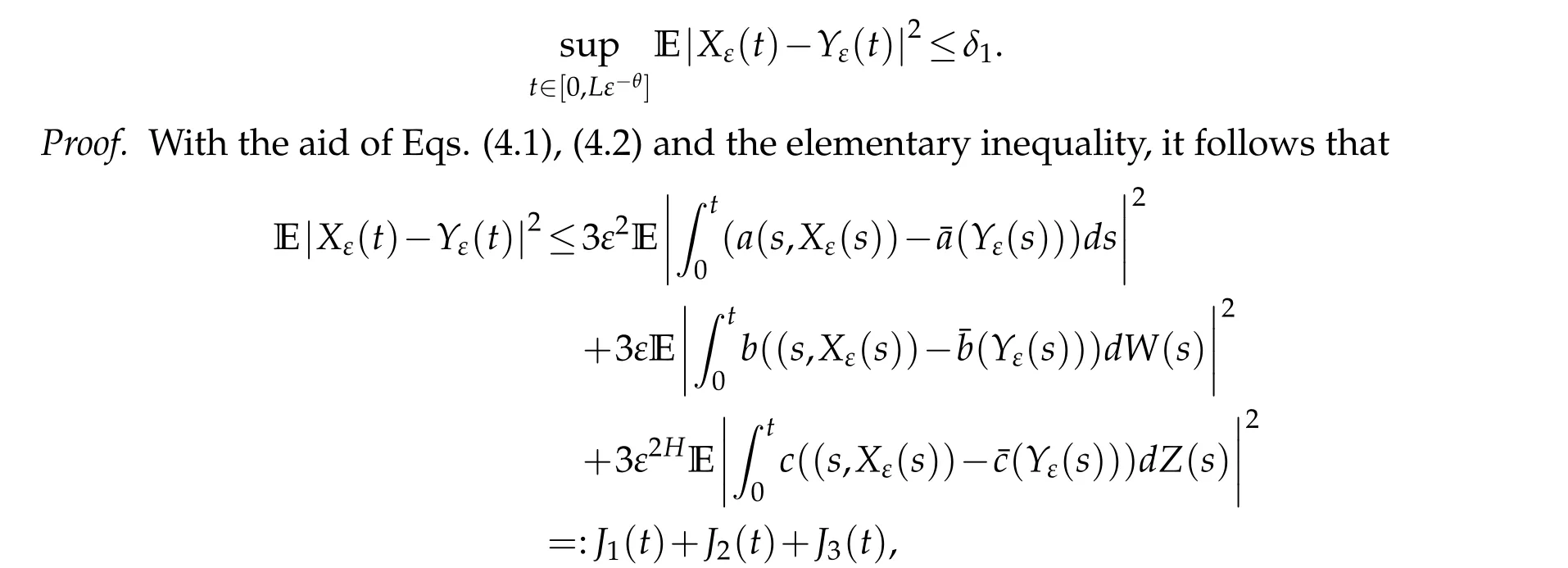



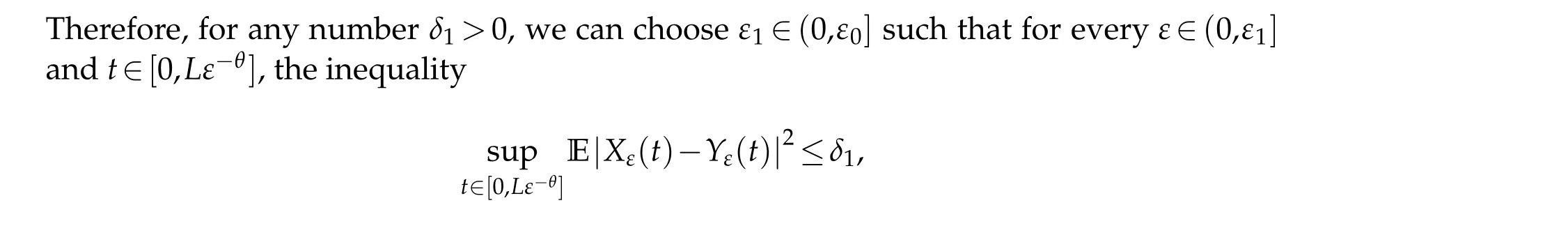
杂志排行
Journal of Partial Differential Equations的其它文章
- Global Well-Posedness of Solutions to 2D Prandtl-Hartmann Equations in Analytic Framework
- Study of Stability Criteria of Numerical Solution of Ordinary and Partial Differential Equations Using Eulers and Finite Difference Scheme
- Infinitely Many Solutions for the Fractional Nonlinear Schr¨odinger Equations of a New Type
- Asymptotic Behavior of Solutions for the Porous Media Equations with Nonlinear Norm-type Sources
- A Weighted Singular Trudinger-Moser Inequality
- Mean Field Equations for the Equilibrium Turbulence and Toda Systems on Connected Finite Graphs
