Study of Stability Criteria of Numerical Solution of Ordinary and Partial Differential Equations Using Eulers and Finite Difference Scheme
2022-12-29AHMADNajmuddinandCHARANShiv
AHMAD Najmuddin and CHARAN Shiv
Department of Mathematics,Faculty of Science Integral University,Kursi Road,Lucknow-226026 Uttar,Pradesh,India.
Abstract. In this paper we have discussed solution and stability analysis of ordinary and partial differential equation with boundary value problem. We investigated periodic stability in Eulers scheme and also discussed PDEs by finite difference scheme.Numerical example has been discussed finding nature of stability. All given result more accurate other than existing methods.
Key Words: Stability; ordinary and partial differential equations; Eulers and finite difference scheme.
1 Introduction
Mathematics is a language which can describe patterns in everyday life as well as abstract concepts existing only in our minds. Patterns exist in data, functions, and sets constructed around a common theme, but the most tangible patterns are visual. Applications of mathematical concepts are also rich sources of visual aids to gain perspective and understanding. Differential equations are a natural way to model relationships between different measurable phenomena. Differential equations do just thatafter being developed to adequately match the dynamics involved. For instance, we are interested in how fast different parts of a frying pan heat up on the stove. Derived from simplifying assumptions about density,specific heat,and the conservation of energy,the heat equation will do just that! I we use the heat equation called a test equation,as a control in our investigations of more complicated partial differential equations(PDEs). [1–3]
2 Stability analysis of single step method
The analytical solutionu(tj)of the differential equation,the difference solutionujof the difference equation and the numerical solution ¯ujcan be related by a relation of the form
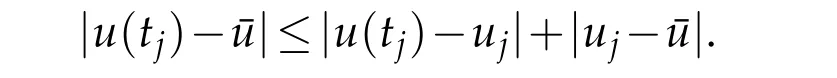
We find that this difference depends on the values|u(tj)−uj|and|uj−¯u|. The value|u(tj)−uj|is the truncation error which arises because the differential equation is replaced by the difference equation. A method is said to be consistent if it is at least of order 1.For a consistent method, the truncation error tends to zero as h approaches zero. The numerical error|uj−¯u| arises because in actual computation, we cannot compute the difference solution exactly as we are faced wit the round off errors. In fact,in some cases the numerical solution may differ considerable from the difference solution. If the effect of the total error including the round-off error remain bounded asj→∞with fixed step size, then the difference method is said to be stable, otherwise unstable[4–6]. Consider the equation
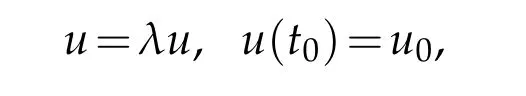
whereλmay be real or complex number. The analytical solution of the equation satisfies the equation
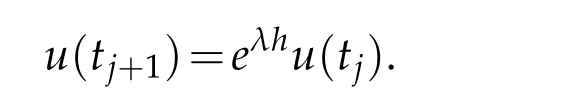
If we apply any single step method to solve the test equation then we get a first order difference equation of the form

The first term of the right hand side is the local truncation error and the second term on the right hand side is the error propagated from the steptjtotj+1. The error on the next steptj+2satisfies the equation,
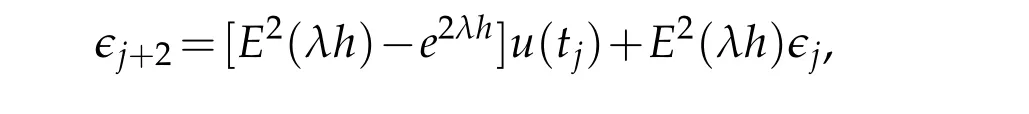
where again first term of the right hand side is the local truncation error and the second term on the right hand side is the propagated error. The errors in computations do not grow, if the propagated error tends to zero or is at least bounded.We call a single step method,when applied to the test equationu=λu.
Absolutely stable if|E(λh)|≤1,λ<0.Relatively stable if|E(λh)|≤eλh,λ>0.Periodically stable if|E(λh)|=1,λis pure imaginary.
Asymptotically stable(A-stable)ifuj →0 asj →∞. This implies that the stability interval ishλ ∈(−∞,0)that is the entire left halfλhplane. whenλ<0,the exact solution decreases as t increases and the necessary condition is absolute stability,since the numerical solution must also decreases with t. Whenλ>0 the exact solution increases with t and we do not need the condition|E(λH)|≤1,so that the relative stability is the necessary condition to be satisfied. Whenλis pure imaginary and|E(λh)|=1, the absolute stability is called periodic stability(p-stability)[4,7].
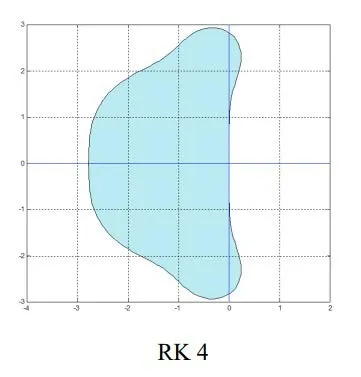
3 Stability Analysis of fourth order Runge-Kutta method

whereas the growth factor of the exact solution iseλh. Ifλh>0,thene(λh)≥E(λh);so the forth order Runge Kutta method is always relatively stable. However ifλh<0, then to find the interval of absolute stability[7,8].
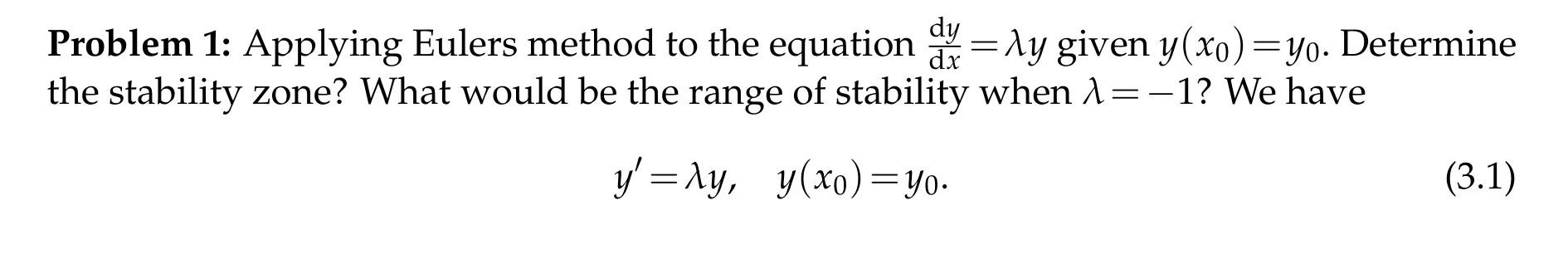
By Eulers method
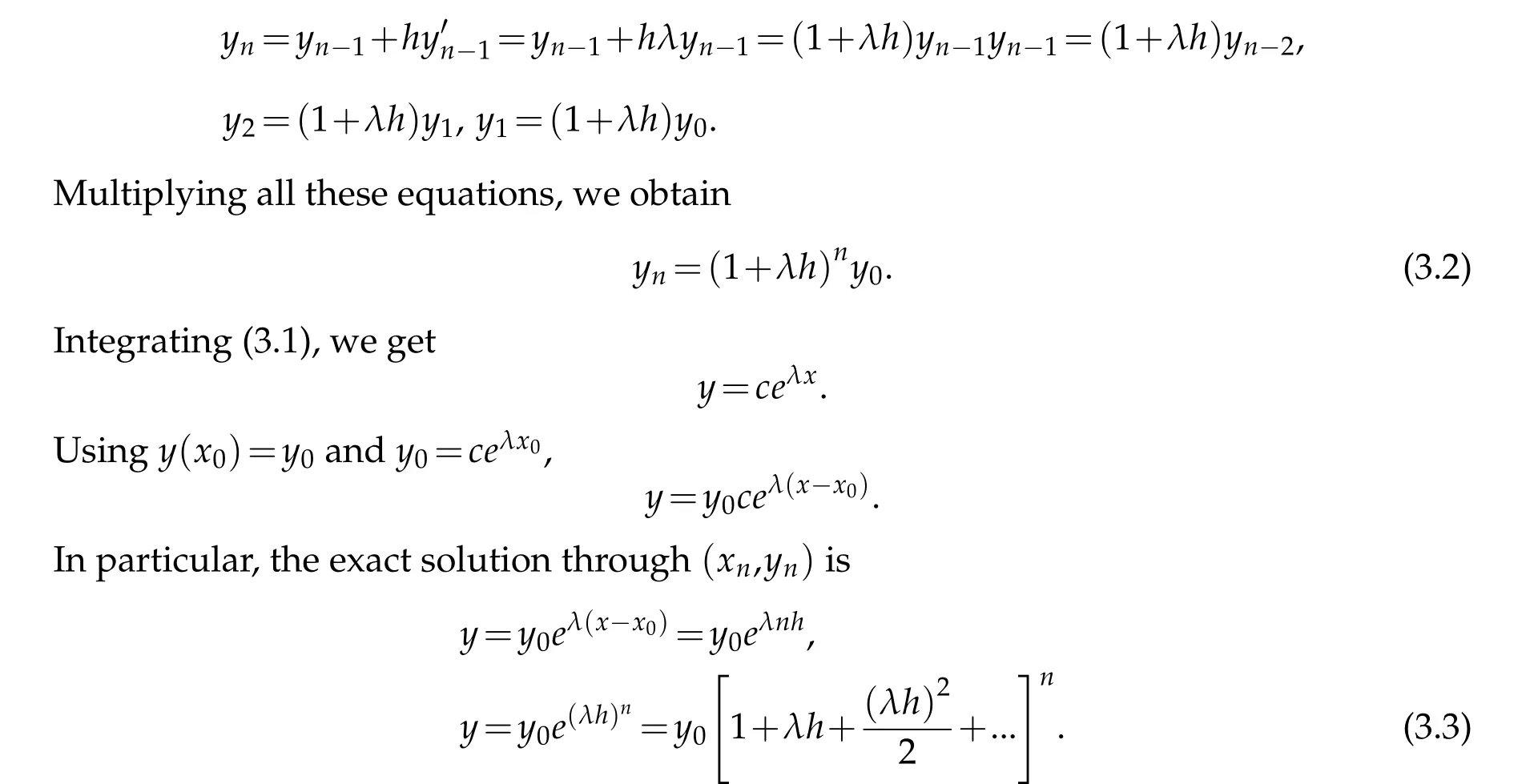
Clearly,the numerical solution(3.2)agree with exact solution(3.3)for small value ofh.The solution(3.2)increases if|1+λh|>1. Hence|1+λh|>1 define a stable zone.
Whenλis real,then the method is stable if|1+λh|>1,i.e.−2<λh<0.
Whenλis complex,then it is stable if|1+(a+ib)h|>1,i.e. 1+ah2+bh2<1,
i.e.,1+x2+y2<1, wherex=ah,y=bh,i.e.,λhlies within unit circle shown in above figure.

Figure 1:
Whenλis imaginary (=ib),|1+λh|=1, then we have a periodic stability. Hence Eulers method is absolutely stable if and only if
1. realλ:−2<λh=0.
2. complexλ:λhlies within unit circle. Eulers method is conditionally convergent.Whenλ=−1,the solution is stable in the range−2<−h<0,i.e.,0 whereAandBare arbitrary constants to be determined by imposing boundary conditions. Ifk>0 andx→∞then the solution become bounded. The terme−kxis monotonic fork>0 andk<0. Thus we except the finite difference is also monotonic fork>0 andk<0.If the behavior of the exponential term of To investigate the stability of finite difference method to solve partial differential equations,we consider whereξ=eαkandαis in general, a complex constant. The finite difference equation will be stable if|up,q| remain bounded forqk ≤T,0≤t ≤T,Tis finite as h→0,k →0,and for all values ofβ, those satisfy the initial conditions. If the exact solution of the finite difference equation does not increase exponentially with time, then a necessary and sufficient condition for stability is that|ξ|≤1,i.e.−1≤β≤1. But,ifup,qincreases with time,then the necessary and sufficient condition for stability is wherea=1−2r2sin2(βh/2),r=k/hthata ≤1 because r,k andβare real. Ifa<−1,then|ξ2|>1 and lead to instability,when−1≤a ≤1,a2≤1 thenξ1andξ2are imaginary and they are given by, This givesr=k/h≤1. This condition is also a sufficient condition. Above result and discussion established that Euler’s method has been conditionally convergent Runge-Kutta method is always relatively stable.In partial differential equation stability investigate finite difference scheme be unconditionally stable and always stable.This research becomes more useful for further study for stability criterion for numerical solutions of ODE and PDE. Acknowledgement Manuscript communication number(MCN):IU/R&D/2018-MCN00677 office of research and development Integral University,Lucknow.4 Stability of finite difference method
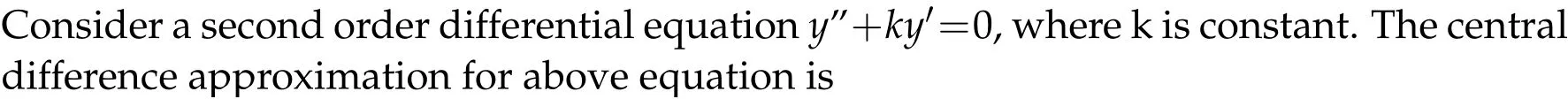
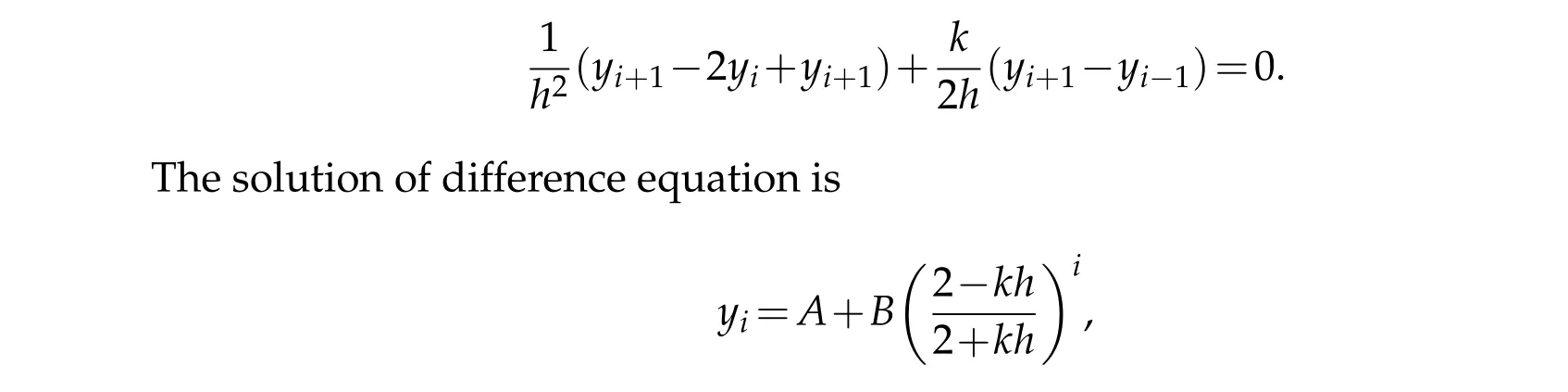


5 Stability region for partial differential equations




6 Conclusion
杂志排行
Journal of Partial Differential Equations的其它文章
- Global Well-Posedness of Solutions to 2D Prandtl-Hartmann Equations in Analytic Framework
- Infinitely Many Solutions for the Fractional Nonlinear Schr¨odinger Equations of a New Type
- Asymptotic Behavior of Solutions for the Porous Media Equations with Nonlinear Norm-type Sources
- Stochastic Averaging Principle for Mixed Stochastic Differential Equations
- A Weighted Singular Trudinger-Moser Inequality
- Mean Field Equations for the Equilibrium Turbulence and Toda Systems on Connected Finite Graphs
