高压填料塔内脱碳传质模型的建立及适用性分析

花亦怀，刘云飞，王 铭，桑 伟，唐建峰，陈 静，姚宝龙，孙培源

（1.中海石油气电集团有限责任公司技术研发中心，北京 100027；2.中国石油大学（华东） 储运与建筑工程学院，山东 青岛 266580；3.北京市煤气热力工程设计院有限公司，北京 100032）

天然气作为一种优质、高效的清洁能源，在中国能源结构中的占比保持上升趋势。“十四五”规划中，采用天然气替代煤炭和汽、柴油，将是防治大气污染的重要途径[1]。采出天然气中含有CO2，会造成管道腐蚀、热值降低等问题，因此脱除CO2等酸气成为天然气预处理中的重要环节。脱除天然气中CO2的方法主要有化学吸收法和变压吸附法等。其中，利用醇胺溶液作为化学吸收剂的胺法脱碳工艺，因具备气体处理量大、运行成本低和技术较成熟等优点，目前应用较多，发展迅速[2-3]。填料塔是胺法脱碳工艺中的关键设备之一，通过相关理论建立填料塔传质模型，是研究其传质性能的重要手段。

目前经典的传质理论主要包括双膜理论[4]、表面更新理论[5]和渗透理论[6]。其中，表面更新理论和渗透理论虽然与实际的传质过程更为接近，但是，相关参数（例如气液接触时间、表面更新率）很难获得。因此，在目前的应用中普遍采用双膜理论。双膜理论于20世纪20年代由WHⅠTMAN[4]提出。其基本观点为，当气液两相相互接触时，两相界面处会出现稳定的层流膜，包括厚度为δg的气膜层与厚度为δL的液膜层。在膜层内，气液两相作层流流动；在膜层之间，物质传递以分子扩散的形式从气相进入液相，气液两相浓度在界面上处于平衡状态，界面传质阻力为零；在膜层外，两相主流区流体充分流动，物质以对流扩散形式进行扩散，传质阻力不计。

在传质性能方面，已有部分学者对胺法脱碳的传质过程进行了合理简化，建立了传质模型，并利用数值模拟与实验相结合的方法，对吸收过程进行研究。MOⅠOLⅠ等[7]利用改进后的Aspen Plus作为建模框架，建立了规整填料塔内哌嗪（PZ）脱碳的传质模型，从温度分布和CO2浓度分布两方面，描述了PZ溶液吸收CO2过程中的传质行为。NAAMⅠ等[8]使用实验室规模的DX规整填料塔，对比了单乙醇胺（MEA）、N-甲基二乙醇胺（MDEA）和叔氨基醇4-二乙氨基-2-丁醇（DEAB）吸收CO2的传质性能，建立了总传质系数随工艺参数变化的经验关联式，发现DEAB溶液具有良好的传质系数，高于MDEA但低于MEA。KHAN等[9]开发了一种基于速率的CO2吸收模型，用于预测填料塔内乙醇胺溶液捕集烟气中CO2的传质过程，与实验结果有良好的一致性。SAⅠDⅠ等[10]基于表面更新理论，建立了规整填料塔内MDEA + PZ混合水溶液CO2吸收速率的数值模型，该模型能够较准确地预测CO2分压在4~16 kPa范围内，混合胺水溶液的吸收速率和传质系数。

以上研究主要针对吸收压力低、CO2浓度低的工况。随着近年来我国天然气工业快速发展，高含CO2天然气田被不断勘探。国内某天然气处理陆上终端的原料气中，CO2含量高达35%（体积分数），且气田开采出的天然气压力较高，对气液物性有一定影响。吸收高浓度CO2过程中，填料塔内CO2浓度和温度梯度沿轴向变化较大，改变了CO2在醇胺溶液中的溶解和扩散性能[11]。因此，建立高压、高浓度CO2下，填料塔内传质模型具有重要意义。本文基于双膜理论，以自主搭建的θ环填料塔为基础，建立适用于高压、高浓度CO2原料气条件下，填料塔内MDEA + PZ脱碳传质模型。引入传质通量修正因子对模型进行修正，在不同进气、溶液流量下，对模型的适应性进行分析，以期为相应特征天然气的净化提供借鉴。

1 传质模型的建立

1.1 物理模型

设定醇胺溶液各组分的质量分数为36% MDEA+ 4% PZ + 60% H2O，初始流量为 40 mL/min，醇胺溶液进入吸收塔时由预热器加热至50 ℃。原料气体各组分的体积分数为 35% CO2+ 65% N2，流量为7.5 L/min，温度为 25 ℃，其中N2不与醇胺溶液反应。

基于自主搭建的小型θ环填料塔，建立物理模型。填料塔内径为38 mm，壁厚为4 mm，材质为304不锈钢。吸收塔内装填有直径为3 mm的316SSθ网环，填料高度为 1500 mm。将填料塔沿轴向分割为微元，填料塔理论物理模型如图1所示。由图1可知，通过气体质量流量控制器调节流量，气相由塔下部进入填料塔，液相经平流泵由塔上部流入填料塔，气液两相在吸收塔内逆流接触，在填料表面提供的有效传质面积上进行传质。气液两相在填料塔中的流动过程为稳态轴对称流动。在同一传质单元内，假定气液两相能够达到完全混合，则在模型建立过程中暂不考虑轴向反混。随传质过程的进行，沿填料吸收高度，气、液流量及浓度不断变化，而气相中的N2流量不发生改变，只有CO2被溶剂吸收，忽略液相溶剂的挥发。

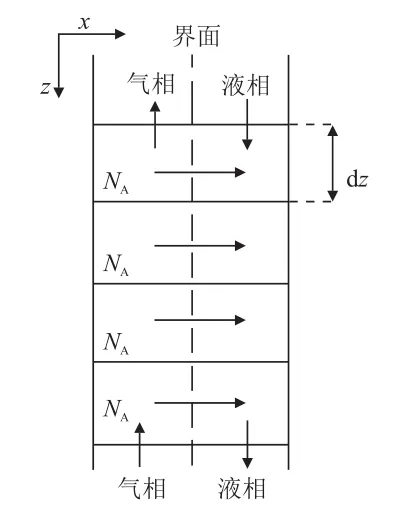
图1 填料塔物理模型Fig.1 Physical model of packed tower

填料微元内的CO2传质通量，可在气液界面处用菲克定律表示如式(1)。填料微元间，气、液相进出口浓度cA、cB分别由式(2)和式(3)求得。

式中，NA为CO2传质通量，mol/(m2∙s)；DA为CO2在溶液中的扩散系数，m2/s；cA为液膜中CO2的浓度，mol/L；x为扩散距离，m；dV为微元填料体积，m3；aV为填料有效传质比表面积，m2/m3；G、L分别为气相、液相摩尔流量，kmol/s；下标A、B分别代表气、液相中的活性组分CO2、醇胺；下标j、j+1代表每个微元间的传质前、传质后。

1.2 数学模型

1.2.1 控制方程

（1）质量守恒方程

基于双膜理论，气相与液相在液膜内逆流接触，吸收过程存在化学反应。在单位传质单元dz中，对醇胺溶液吸收CO2的传质过程进行物料衡算。CO2由气相主体进入液相为x正方向。在MDEA +PZ吸收CO2过程中，PZ在液膜中穿梭，主要起活化作用。因此，该过程将PZ及MDEA视作一种醇胺，可得式(4)。在单位填料dz内dx方向上，对醇胺溶液吸收CO2进行物料衡算，根据菲克定律，得到关系式(5)。气液接触传质过程中，PZ能够将CO2较快地转移给MDEA进行反应，因此假定液膜中PZ的浓度基本不变，总反应速率rA计算如式(6)。由双膜理论中的假设，可知控制方程的边界条件如式(7)和式(8)。联立式(5)和式(6)，并进行化简得式(9)。则单位传质单元dz中，CO2的质量守恒方程为式(10)。

式中，YCO2为传质单元内气相CO2的体积浓度，L/m3；rA为总反应速率；k为速率常数；cAl为CO2在界面处的浓度，mol/L；cBl为MDEA在液相主体的浓度，mol/L；H为亨利常数，L∙kPa/mol；p为压力，kPa；δ为CO2由界面进入液相主体的距离，m。

（2）能量守恒方程

填料塔轴向方向任一填料微元dz，其能量守恒关系引用李虎等[11]文中所述，并进行修正。微元填料内，流出微元的能量为流入微元的能量与微元内化学反应的放热量之和。其中，流入微元填料的能量Er如式(11)所示，流出的能量Ec如式(12)所示，化学反应热Qf如式(13)所示，根据守恒关系式化简得式(14)，其定解条件为式(15)。

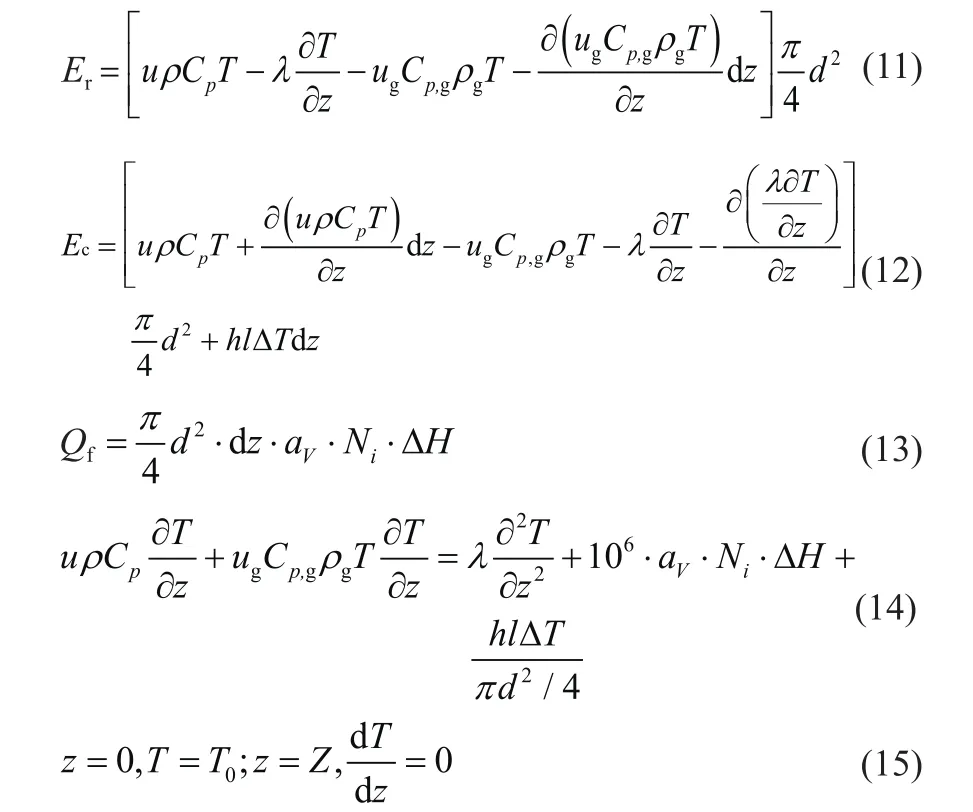
式中，u、ug分别为液相、气相流速，m/s；ρ、ρg分别为液相、气相密度，kg/m3；Cp、Cp,g分别为液相、气相定压比热容，J/(kg∙K)；λ为液相导热系数，W/(m∙K)；T为温度，K；Ni为传质通量，mol/(m2∙s)；ΔH为反应生成焓，J/mol；h为对流散热系数，W/(m2∙K)；z为高度，m；Z为填料塔高度，m；l为填料塔周长，m；d为填料塔直径，m。

1.2.2 传质模型参数

（1）物质物性

MDEA、PZ和H2O的物性参数如表1所示。

表1 物性参数Table 1 Physical parameters

在吸收压力为 0.1 MPa时，MDEA、PZ和H2O的定压比热容拟合公式[13]如下。

（2）物理溶解度及扩散系数

CO2与醇胺溶液会发生化学反应，故不能直接测量CO2在醇胺溶液中的物理溶解度和扩散系数。因此，需使用非反应性气体N2O替代CO2，利用“N2O类比法”估算，如式(19)和式(20)所示。用于计算CO2及N2O物理溶解度的相关公式如表2所示。用于计算气、液相扩散系数的相关公式如表3所示。

表2 CO2及N2O物理溶解度计算公式Table 2 Calculation formulas for physical solubility of CO2 and N2O

表3 CO2及N2O扩散系数计算公式Table 3 Calculation formulas for diffusion of CO2 and N2O

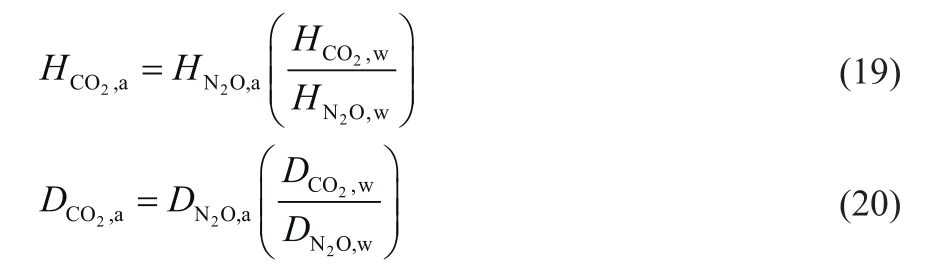
式中，HCO2,a、HN2O,a分别为CO2、N2O在醇胺溶液中的物理溶解度，L∙kPa/mol；HCO2,w、HN2O,w分别为CO2、N2O在纯水中的物理溶解度，L∙kPa/mol；DCO2,a、DN2O,a分别为CO2、N2O在醇胺溶液中的扩散系数，m2/s；DCO2,w、DN2O,w分别为CO2、N2O在纯水中的扩散系数，m2/s。

表4 二元醇胺溶液N2O扩散系数相关性参数Table 4 Correlation parameter of N2O diffusion coefficient of binary alkanolamine solution

（3）反应速率常数

PZ活化的MDEA溶液吸收CO2，其反应机理[18-19]如式(21)~式(26)所示，其中R1R2R3N代表MDEA，R1、R2代表—C2H4OH，R3代表—CH3。式(21)为MDEA作为碱催化水吸收CO2的过程。式(22)为PZ与CO2反应生成氨基甲酸盐产物PZCOO-的过程，SAMANTA等[20]研究表明，PZ与CO2反应，和MDEA吸收CO2反应过程平行，均为拟一级快速反应。式(23)可以理解为，在活化过程中，PZ与扩散进入液膜的CO2结合形成PZ-CO2，快速地将CO2转移给MDEA并进行下一步反应。式(24)为PZCOO-与MDEA进行反应，将CO2转化为碳酸氢盐，同时PZ在此反应中被还原，被还原的PZ迅速接受扩散进入液膜的CO2，PZ的活化效应得到显现。由于PZ分子含有 2个氨基，式(25)理论上会发生，但LⅠU等[21]认为可以忽略该反应。式(26)的平衡常数很小，反应过程中几乎不起作用，相关反应动力学文献[22-23]中均做忽略处理。

（4）动力黏度

MDEA+PZ混合醇胺溶液的动力黏度采用Weiland方程进行计算，如式(29)和式(30)所示。

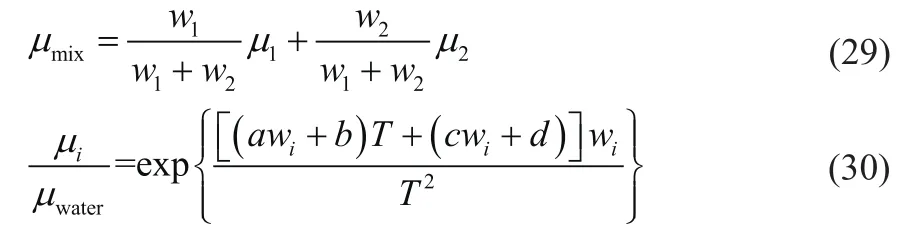
式中，μi为溶液动力黏度，mPa∙s；a、b、c和d为参数，数值见表5。

表5 Weiland方程模型参数[26]Table 5 Model parameters of Weiland equation[26]

（5）导热系数

标准大气压下，纯MDEA的导热系数由式(31)计算。气液在填料塔吸收过程中未达到饱和状态，则取水为过冷水状态，其常压下导热系数由LEMMON[27]提供的数据进行拟合，得到的四阶公式如式(32)所示。由5~90 ℃相关实验数据，拟合得到PZ导热系数的二阶公式，如式(33)所示。对于三元体系的液体混合物，由秦正龙等[28]提供的公式(34)计算，其中Kij为作用矫正系数，如式(35)所示。具体计算过程为，获得组分物质的导热系数，根据组分的质量分数计算出混合液体的导热系数。

式中，Uij为组分i与j导热系数的比值，其中数值大者做分母，故Uij<1；下标m代表混合液体。

1.3 模型的计算流程

计算高压下填料塔内MDEA + PZ脱碳传质模型。首先假设填料塔上部气相中CO2的浓度值（体积分数，下同），对于第一个传质单元，已知MDEA +PZ醇胺溶液浓度及温度，将传质单元内质量守恒方程，在x方向进行离散并带入边界条件，通过TDMA（The tridiagonal matrix algorithm）法求得传质单元内气、液相浓度，利用菲克定律得到下一传质单元气相出口浓度和液相入口浓度。对能量守恒方程在z方向进行离散并带入边界条件，利用TDMA法得到传质单元的温度。自塔上部至下部，依次计算每一传质单元内气、液相浓度及温度。将求解的模型中，填料塔下部最终CO2浓度与已知的入塔CO2浓度进行比较，如果计算值高，则重复该过程，如果计算值低，则增加初始CO2浓度假设值，直到与底部的CO2浓度相等为止。利用C语言计算机编程软件，对上述过程进行编程，如图2所示。通过迭代运算，得到填料塔数值模型中CO2浓度场及温度场。

图2 填料塔传质模型计算流程Fig.2 Computing procedure of mass transfer model for packed tower

2 模拟结果及模型修正

将得到的模型用于高压条件下，MDEA + PZ混合溶液CO2吸收性能的模拟分析。但高压吸收过程中，沿填料塔总气体流速显著下降，会导致不同传质单元间传质通量较实际情况有所不同。因此，需要对模型进行修正。

2.1 不同吸收压力下模拟与实验结果

利用初步搭建的脱碳传质模型，控制模型中其他参数不变，在吸收压力为常压、1 MPa、2 MPa、3 MPa和 4 MPa时，分别进行了实验与模拟计算，结果见图3。由图3可知，高压下模拟得到的，填料塔中CO2浓度曲线和温度曲线，与实验数据差异较大。同时，随吸收压力的提高，误差逐渐增大，CO2浓度最大误差为86.64%，温度最大误差为28.63%。

图3 不同吸收压力下填料塔内CO2浓度(a)和温度(b)分布Fig.3 Distribution of CO2 concentration (a) and temperature (b)in packed tower under different absorption pressures

2.2 引入传质通量修正因子

针对上述问题，引入传质通量修正因子F，对较高吸收压力下的传质模型进行了修正[29]。F计算方法为，在相同压力下，以填料塔高度为X轴，CO2浓度为Y轴，输入不同节点的实验值及模拟值，二者作商，其值用MATLAB进行二阶拟合得到二阶拟合函数。温度场亦用相同方法进行处理。将温度场和浓度场对比后的拟合函数，以填料塔高度为X轴，输出Y值二者相加取平均值，再次进行二阶拟合得到拟合函数。最后以填料塔高度为X轴，输出Y值相加得到均值，即为F值。高压下单位传质单元内引入F后，传质通量NA1如式(36)所示。

以吸收压力4 MPa为例，综合考虑填料塔CO2浓度场、温度场模拟值及实验值间的均方误差，当F为0.2315时，均方误差达到最低，见图4。由图4可知，填料塔内CO2浓度模拟与实验结果间最大误差为9.75%，温度最大误差为3.03%，模型准确性显著提高。基于不同吸收压力下填料塔CO2浓度及温度场实验值，对建立的传质模型进行了修正，得到0.1~4.0 MPa下F值曲线如图5所示。

图4 模型修正后4 MPa下填料塔内CO2浓度(a)和温度(b)分布Fig.4 Distribution of CO2 concentration (a) and temperature (b) in packed tower under 4 MPa after model correction

图5 不同吸收压力下F值曲线Fig.5 F value curve under different absorption pressures

3 模型适用性分析

实际生产中，输送到脱碳装置的原料气气量处于波动状态，为探究工艺参数对MDEA + PZ吸收CO2过程中传质行为的影响，基于国内某终端天然气处理厂现场气液比，及自主搭建的小型θ环填料塔装置最大处理量，选择不同进气、溶液流量，对传质模型的适用性进行分析。

3.1 不同进气流量下模型的适用性

利用修正的高压填料塔内MDEA+PZ脱碳传质模型，控制模型中其他参数不变，探究了模型不同进气流量下的适用性。在进气流量为5.5 L/min、6.5 L/min、7.5 L/min、8.5 L/min和 9.5 L/min时，分别进行了模拟计算，并且与实验结果进行对比，结果见图6。由图6(a)可知，进气流量从5.5 L/min提升至9.5 L/min，模拟得到的填料塔中CO2浓度曲线，与实验测得的趋势较为一致，最大误差为8.79%。小型θ环填料塔实验装置外侧有保温套，但实际仍存在热量散失，而模型中未考虑填料塔散热。因此，实验测点温度比模拟的稍低，并且越靠近塔底幅度越大，最大误差为2.37%。

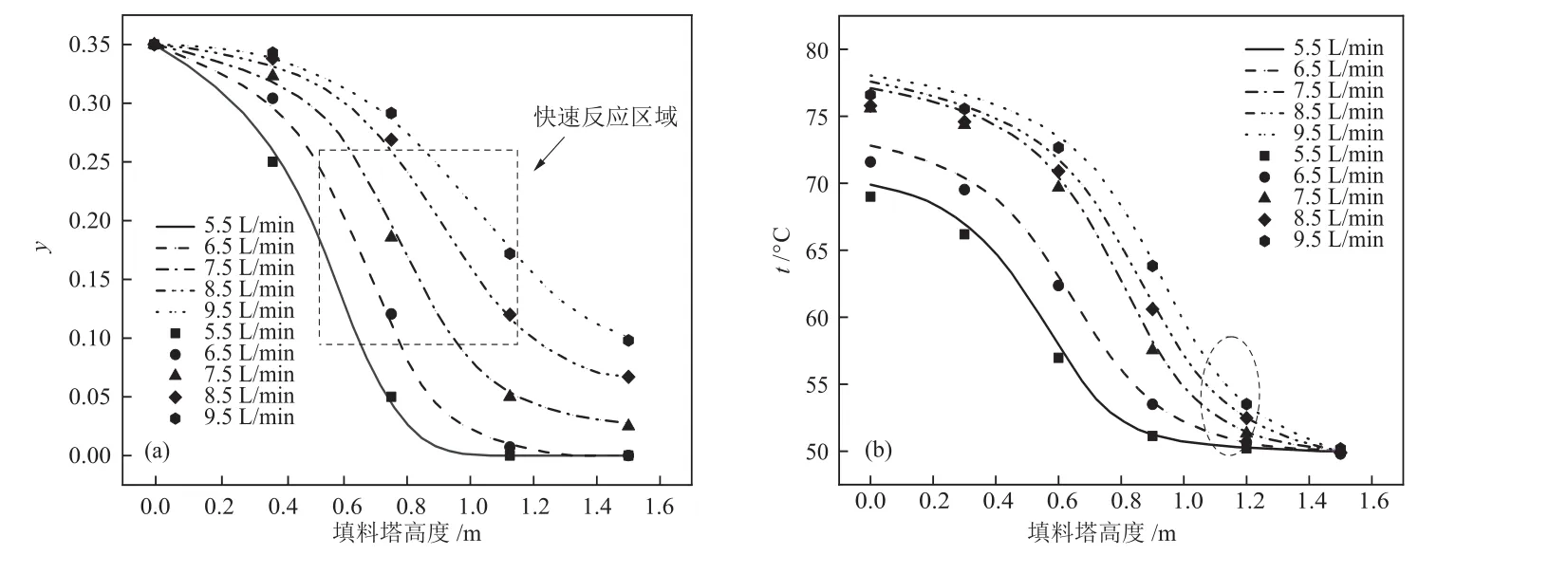
图6 不同进气流量下填料塔内CO2浓度(a)和温度(b)分布Fig.6 Distribution of CO2 concentration (a) and temperature (b) in packed tower under different inlet gas flow rates

进一步分析可知，填料塔内存在一个快速反应区域。该区域内，气、液相传质阻力的变化趋势相反，使得反应速率几乎不变。进气流量增大会使该区域向塔顶移动，而其他区域由于某一相传质阻力相较于另一相过大，导致了反应速率快速下降。由图6(b)可知，进气流量增大会改善填料塔内的温度分布。

3.2 不同溶液流量下模型的适用性

控制模型中其他参数不变，探究了模型不同溶液流量下的适用性。在溶液流量为30 mL/min、35 mL/min、40 mL/min、45 mL/min和 50 mL/min时，进行了模拟计算，并与实验结果进行了对比，结果见图7。由图7可知，随着溶液流量从30 mL/min提升至50 mL/min，模拟得到的填料塔中CO2浓度曲线，与实验测得的趋势较为一致，最大误差为5.39%；从塔顶到塔底，温度的模拟值与实验值差距逐渐增大，最大误差为1.98%。

图7 不同溶液流量下填料塔内CO2浓度(a)和温度(b)分布Fig.7 Distribution of CO2 concentration (a) and temperature (b) in packed tower under different solution flow rates

进一步分析可知，溶液流量增大会使填料塔内快速反应区向塔顶移动，其他规律与不同进气流量下的结果类似。溶液流量为50 mL/min时，塔底的最高温度比 35 mL/min、40 mL/min和 45 mL/min时低，说明溶液流量已经高于完全处理原料气中CO2所需要的流量，这与图7(a)得到的结果是相对应的。

4 结论

本文以自主搭建的小型θ环填料塔实验装置为基础，采用TDMA算法，基于双膜理论，结合物理溶解度及扩散系数、反应速率常数、运动黏度和导热系数等参数，建立了填料塔内MDEA + PZ脱碳传质模型。通过引入传质通量修正因子，对高压下传质模型的准确性进行修正，并考察了不同进气和溶液流量下，模型的适应性，得到如下结论。

（1）使用初步搭建的模型，高压下模拟得到的填料塔中的CO2浓度曲线和温度曲线，与实验数据差别较大，且随吸收压力增大而提高，CO2浓度最大误差为86.64%，温度最大误差为28.63%。

（2）引入传质通量修正因子，对脱碳传质模型进行修正，得到了不同吸收压力下F的拟合曲线。模型修正后适用于高压工况，填料塔内CO2浓度模拟与实验结果最大误差降至9.75%，温度的最大误差降至3.03%。

（3）不同进气和溶液流量下，模型计算值与实验数据趋势较为一致。填料塔内，温度场最大误差为2.37%、CO2浓度场最大误差为8.79%，说明修正后模型的可靠性较强。