利用底边过焦点的阿基米德三角形性质解高考题

甘肃省灵台县第一中学 (744400) 王海燕

阿基米德最早利用逼近思想证明了抛物线的弦与抛物线所围成封闭图形的面积，等于抛物线的弦与过弦端点的两条切线所围三角形面积的三分之二.后来人们称由抛物线的弦与过该弦端点的两切线所围成的三角形为阿基米德三角形.其中该弦称为阿基米德三角形的底边，阿基米德三角形有许多性质，底边过焦点的阿基米德三角形有如下常见结论：

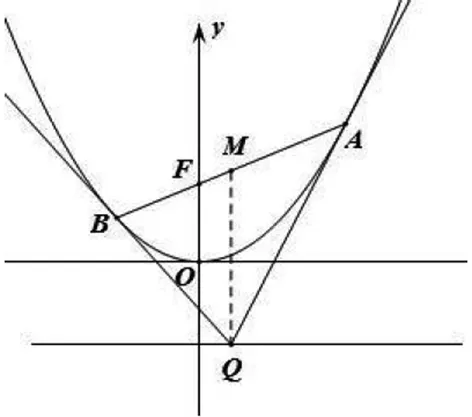
图1

如图1，AB是过抛物线C:x2=2py焦点F的弦，C在点A，B处的切线QA,QB交于Q点，点M(x0,y0)为AB的中点.△QAB即为阿基米德三角形，其中AB为阿基米德三角形的底边，则

(1)切线QA,QB的交点Q在抛物线C的准线上;

(2)底边上的中线平行于抛物线的对称轴，即xQ=x0;

(3)△QAB是直角顶点在抛物线准线上的RtΔ，即AQ⊥BQ;

(4)FQ⊥AB;

(5)阿基米德三角形面积的最小值为p2.

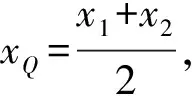
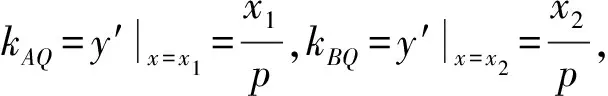
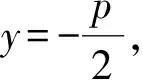
事实上，利用上述结果有如下结论：

结论1 若切线QA,QB的交点Q在抛物线C的准线上，则抛物线C的弦AB必过焦点.即命题(1)的逆命题也成立.

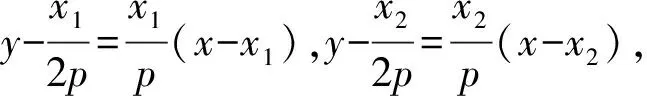
结论2 阿基米德三角形底边上的中线平行于抛物线的对称轴.即结论(2)可推广到一般的阿基米德三角形.(证略.)

结论3 若A(x1,y1)，B(x2,y2)，中点M(x0,y0)，则阿基米德三角形QAB的底边AB所在直线方程为(x1+x2)x+-2py-x1x2=0；若AB过焦点，则可化为2x0x-2py+p2=0；切线QA，QB的方程分别为x1x=p(y+y1)，x2x=p(y+y2).(证略.)

例1 (2014·辽宁卷)已知点A(-2,3)在抛物线C:y2=2px的准线上，过点A的直线与C在第一象限相切于点B，记C的焦点为F，则直线BF的斜率为( ).

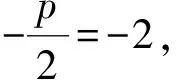
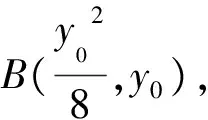
例2 (2018·新课标Ⅲ卷)已知点M(-1,1)和抛物线C:y2=4x，过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°，则k=.

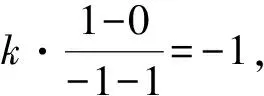
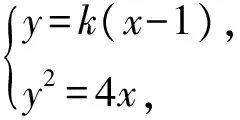
再如，(2021全国乙卷，理21)已知抛物线C:x2=2py(p>0)的焦点为F，且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.

(1)求p；

(2)若点P在M上，PA,PB是C的两条切线，A,B是切点，求△PAB面积的最大值.

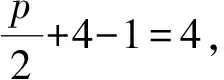
(2)△PAB是一般的阿基米德三角形，但可依性质(1)的证明方法，利用导数求出直线PA，PB，进一步可求得直线AB的方程，将直线AB的方程与抛物线的方程联立后，依弦长公式表示出|AB|及点P到直线AB的距离，把△PAB的面积表示成P点纵坐标y0的二次函数，由-5≤y0≤-3，可求得△PAB面积的最大值.

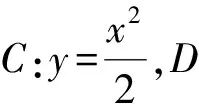
(1)证明：直线AB过定点；

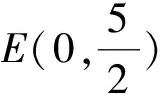
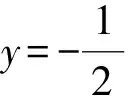
(2)略.

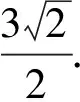
(1)求抛物线C的方程；

(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程；

(3)当点P在直线l上移动时,求|AF|·|BF|的最小值.

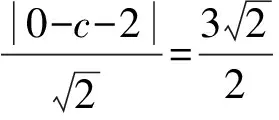
(2)△PAB即为阿基米德三角形，设A(x1,y1)，B(x2,y2)，依据结论3可得切线PA,PB的方程为x1x-2y-2y1=0,x2x-2y-2y2=0.由P(x0,y0)在切线PA,PB上,得x1x0-2y0-2y1=0,x2x0-2y0-2y2=0.所以(x1,y1),(x2,y2)为方程x0x-2y0-2y=0的两组解.所以直线AB的方程为x0x-2y-2y0=0.

(3)略.