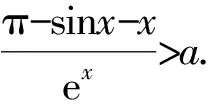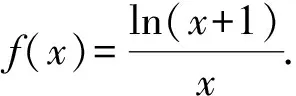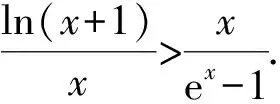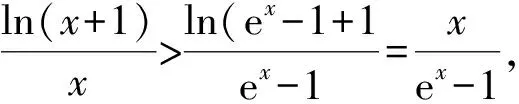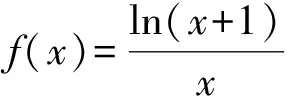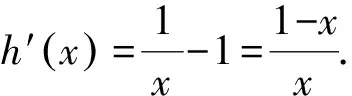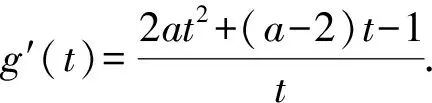对含有ex的函数综合题的解法探究

山东省临沂第四中学 (276000) 李秀萍 梁乾培

含有ex函数的综合试题在高考中出现的频率高，解法灵活，思维含量高，能够很好的区分考生的理性思维品质，而理性思维又是数学核心素养的灵魂.甄别不同层次考生的数学素养，依托关键知识和核心概念命题，体现数学本质，是高考命题的追求.中学数学教学就要通过教学落实核心素养，培养学生的思维能力和水平，掌握数学知识是发展数学核心素养的前提，掌握数学就意味着解题.本文从四个角度对解含有ex函数综合题为例，进行尝试.

1.对ex放缩

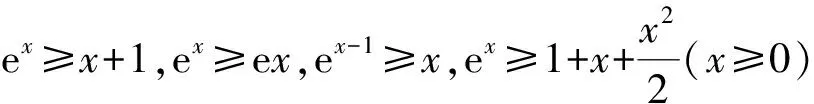
例1 (2020年全国Ⅰ卷理科第21题)已知函数f(x)=ex+ax2-x.

(Ⅰ)当a=1时，讨论f(x)的单调性；

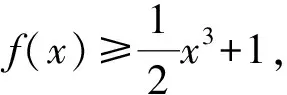
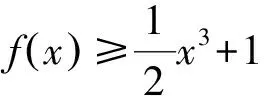
①当x=0时，不等式为1≥1，显然成立，符合题意.

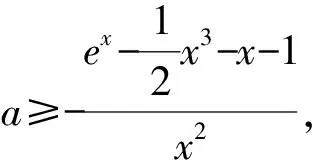
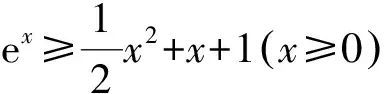
2.给ex找“朋友”

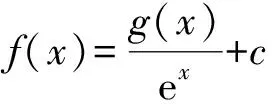
例2 (2018年全国卷Ⅰ文科第21题)已知函数f(x)=aex-lnx-1.

(Ⅰ)设x=2是f(x)的极值点，求a，并求f(x)的单调区间；

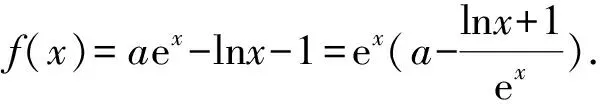
方法点睛：通过改变函数的结构，构造新函数，将参数a分离，把ex与其它函数结合在一起，求导后，导数仍然是ex与一个多项式乘积的形式，这样导数的符号取决于多项式的符号，故只需要研究其他函数的符号即可确定函数的单调性，从而，确定函数的最值(极值)，将复杂的问题简单化.

例3 已知函数f(x) =aex+ sinx+x,x∈[0,π].当-2

方法点睛：通过给ex找朋友，把ex与三角函数结合，求导后，ex对于导数符号没有影响，只需要考虑不含ex的三角函数的符号就可以确定函数的单调性，否则，ex与三角函数混在一起，要多次求导，并且要考虑隐零点的方法，麻烦的多.

3.对ex构造同构式

同构式是指除了变量不同，其余地方均相同的表达式.如果不等式的两侧呈现同构特征，则可将相同的结构构造为一个函数，进而与函数的单调性找到联系，使得问题得到解决.

(Ⅰ)判断f(x)在(0,+∞)的单调性；

(Ⅱ)若x>0,证明:(ex-1)ln(x+1)>x2.

解：(Ⅰ)函数f(x)是(0,+∞)上的减函数.(过程略)

例5 (2020年全国卷(山东)第21题)已知函数f(x)=aex-1-lnx+lna.

(Ⅰ)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(Ⅱ)若f(x)≥1，求a的取值范围.

方法点睛：函数f(x)中含有lna，为了凑出同构式，可将aex-1转化为elna+x-1，即函数f(x)转化为f(x)=elna+x-1-lnx+lna，而要进行同构，往往f(x)有偶数项，因此，按照elna+x-1进行添项和移项，故f(x)>1等价于elna+x-1-lnx+lna>1⟺elna+x-1+(lna+x-1)>lnx+x.从而，构造函数g(x)=ex+x，利用函数的单调性处理.

4.把ex换元，将指数转化为对数

由于指数运算和对数运算是互逆运算，所以可以通过换元，进行指对互化.其目的是将分散的条件联系起来，或把隐含的条件显示出来，或把条件结论联系起来，或化为熟悉的问题.在导数的综合题中，往往通过指对互化来实现函数结构的变换.

例6 (2017年全国Ⅰ卷文科第21题)已知函数f(x)=ae2x+(a-2)ex-x.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若f(x)有两个零点，求a的取值范围.

方法点睛：借助换元，将指数转化为对数，从而改变问题的结构，把原来解析式中含有e2x,ex的表达式转化为二次和一次的代数式，对数的次数为一次，求导之后，导数的分子是一个“类二次函数”，导数符号的确定，函数单调性的研究，我们轻车熟路，大大降低解题的难度.

通过上面的几个例题，我们可以感受到在解决含有ex函数综合题时，要抓住函数的本质，考虑切线放缩(泰勒展式放缩)；改变函数的表述形式，将ex与其它的多项式函数结合，或构造同构式；或将指数转化为对数，化生为熟，化繁为简.含有ex函数综合题解题的思路广、方法灵活、思维含量高，但是，我们要遵循逻辑规律、寻求通性通法，突出变换函数，落实、体会转化与化归思想在解题中的应用，对于形成优良思维品质、开阔解题视野有重要意义.